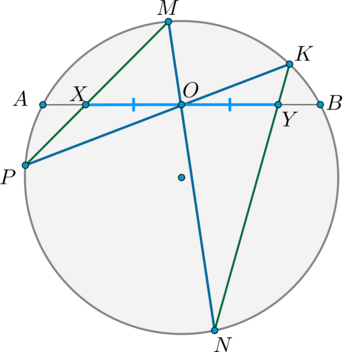
Хорда \(AB\) разбивает окружность \(S\) на две дуги. Окружность \(S_1\) касается хорды \(AB\) в точке \(M\) и одной из дуг в точке \(N\).
Докажите, что прямая \(MN\) проходит через середину \(P\) второй дуги.
Предположим, что прямая \(MN\) пересекает вторую дугу в точке \(P\) и \(P\) – не середина этой дуги. Отметим точку \(P'\) – середину дуги \(\buildrel\smile\over{AB}\).
Рассмотрим \(\triangle MO_1N\) и \(\triangle P'ON\). Они равнобедренные, т.к. \(O_1M=O_1N\) – радиусы окружности \(S_1\), \(OP'=ON\) – радиусы окружности \(S\).
Рассмотрим окружность \(S_1\). Т.к. угол между касательной и хордой, проходящей через точку касания, равен половине дуги, заключенной между ними, то угол между касательной \(AB\) и хордой \(MN\) равен половине дуги \(\buildrel\smile\over{MN}\) (которая меньше полуокружности по рисунку). Обозначим \(\angle AMN=\alpha\). Следовательно, \(\angle MO_1N=2\alpha\), т.к. он центральный, опирающийся на дугу \(\buildrel\smile\over{MM}\), равную \(2\alpha\).
Рассмотрим окружность \(S\). Т.к. \(P'\) – середина дуги \(AB\), то \(\angle AOP'=\angle BOP'\). Следовательно, в равнобедренном треугольнике \(AOB\) \(OP'\) – биссектриса. Следовательно, она и высота, то есть \(OP'\perp AB\). Но \(O_1M\perp AB\) (как радиус, проведенный в точку касания в окружности \(S_1\)), следовательно, обе прямые \(O_1M\) и \(OP'\) перпендикулярны \(AB\), следовательно, они параллельны.
Заметим, что т.к. окружности \(S\) и \(S_1\) касаются, то их центры \(O\) и \(O_1\) и точка касания \(N\) лежат на одной прямой.
Таким образом, \(\angle NO_1M=\angle NOP'=2\alpha\) как соответственные углы при \(O_1M\parallel OP'\) и \(NO\) – секущей.
Значит, \(\angle MNO_1=\frac12\left(180^\circ-2\alpha\right)=\angle P'NO\). А т.к. точки \(N, O_1, O\) лежат на одной прямой, то и точки \(N, M, P'\) лежат на одной прямой. Следовательно, \(P'\) совпадает с \(P\).
Ответ:
Доказательство