\(\blacktriangleright\) Угол \(\alpha\) наклона прямой – это угол между этой прямой и положительным направлением оси \(Ox\) (\(0\leqslant \alpha< 180^\circ\)), лежащий в верхней полуплоскости.

\(\blacktriangleright\) Основная формула. Угловой коэффициент прямой \(y=kx+b\) равен тангенсу угла наклона этой прямой:

\[{\large{\color{royalblue}{k=\mathrm{tg}\, \alpha}}}\]
Т.к. касательная к графику некоторой функции — это и есть прямая, то для нее верны все эти утверждения.

Если \(\alpha<90^\circ\), то \(k>0\);

если \(\alpha>90^\circ\), то \(k<0\);

если \(\alpha=0^\circ\), то \(k=0\) (уравнение прямой имеет вид \(y=b\) и она параллельна оси \(Ox\));

если \(\alpha=90^\circ\), то уравнение прямой имеет вид \(x=a\) и она перпендикулярна оси \(Ox\).

Ознакомиться с полной теорией

Задание 8 #694

Уровень задания: Легче ЕГЭ

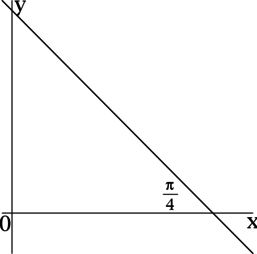
Прямая \(y = kx + 6\) образует угол \(\dfrac{\pi}{4}\) радиан с отрицательным направлением оси \(Ox\). Найдите \(k\).

Показать решение

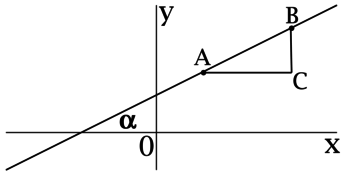
Для прямой, заданной уравнением \(y = kx + b\), коэффициент \(k\) есть значение тангенса угла между прямой \(y = kx + b\) и положительным направлением оси \(Ox\).

Так как угол между прямой \(y = kx + 6\) и отрицательным направлением оси \(Ox\) равен \(\dfrac{\pi}{4}\) радиан, то угол между прямой \(y = kx + 6\) и положительным направлением оси \(Ox\) равен \(\pi - \dfrac{\pi}{4} = \dfrac{3\pi}{4}\) радиан, тогда \(k = \mathrm{tg}\, \dfrac{3\pi}{4} = -1\).

Ответ: -1

Задание 9 #699

Уровень задания: Легче ЕГЭ

Найдите угол \(\alpha\) между прямой \(y = \sqrt{3}x + 3\sqrt{3}\) и положительным направлением оси \(Ox\). Ответ дайте в градусах.

Показать решение

Таким образом, \(\mathrm{tg}\, \alpha = \sqrt{3}\). Так как градусная мера угла между двумя прямыми лежит в полуинтервале \([0; 180^{\circ})\), а \(\mathrm{tg}\, \alpha = \sqrt{3} > 0\), то \(0 < \alpha < \dfrac{\pi}{2}\), следовательно, \(\alpha = \mathrm{arctg}\, (\sqrt{3}) = \dfrac{\pi}{3}\). В итоге \(\alpha = 60^{\circ}\).

Ответ: 60

Задание 10 #692

Уровень задания: Легче ЕГЭ

Прямая \(y = 21x - 6\) образует угол \(\alpha\) с положительным направлением оси \(Ox\), а прямая \(y = -3x\) образует угол \(\beta\) с положительным направлением оси \(Ox\). Найдите \(\mathrm{tg}\, \alpha\cdot\mathrm{ctg}\, \beta\).

Показать решение

Таким образом, \(\mathrm{tg}\, \alpha = 21\), а \(\mathrm{tg}\, \beta = -3\). Так как \(\mathrm{tg}\, \beta \neq 0\), то \(\mathrm{ctg}\, \beta = \dfrac{1}{\mathrm{tg}\, \beta}\), откуда \(\mathrm{ctg}\, \beta = -\dfrac{1}{3}\). Итого: \(\mathrm{tg}\, \alpha\cdot\mathrm{ctg}\, \beta = 21\cdot \left(-\dfrac{1}{3}\right) = -7\).

Ответ: -7

Задание 11 #700

Уровень задания: Равен ЕГЭ

Найдите угол \(\alpha\) между прямой \(y = \dfrac{1}{\sqrt{3}}x - 6\sqrt{64}\) и положительным направлением оси \(Ox\). Ответ дайте в градусах.

Показать решение

Таким образом, \(\mathrm{tg}\, \alpha = \dfrac{1}{\sqrt{3}}\). Так как градусная мера угла между двумя прямыми лежит в полуинтервале \([0; 180^{\circ})\), а \(\mathrm{tg}\, \alpha = \dfrac{1}{\sqrt{3}} > 0\), то \(0 < \alpha < \dfrac{\pi}{2}\), следовательно, \(\alpha = \mathrm{arctg}\left(\dfrac{1}{\sqrt{3}}\right) = \dfrac{\pi}{6}\). В итоге \(\alpha = 30^{\circ}\).

Ответ: 30

Задание 12 #701

Уровень задания: Сложнее ЕГЭ

Точки \(A\) и \(B\) лежат на прямой \(l\). При этом точка \(A\) имеет координаты \((1; 1)\), а точка \(B\) имеет координаты \((3; 2)\). Найдите тангенс угла \(\alpha\) между этой прямой и положительным направлением оси \(OX\).

Показать решение

Достроим треугольник \(ABC\) так, что \(AC \parallel Ox\), \(BC \parallel Oy\) (тогда \(\angle C = 90^{\circ}\))

\(\mathrm{tg}\, \alpha = \dfrac{BC}{AC}\).

Длина отрезка \(AC\) равна модулю разности первых координат точек \(A\) и \(B\), тогда \(AC = 3 - 1 = 2\).

Длина отрезка \(BC\) равна модулю разности вторых координат точек \(A\) и \(B\), тогда \(BC = 2 - 1 = 1\). В итоге \(\mathrm{tg}\, \alpha = \dfrac{BC}{AC} = 0,5\).

Ответ: 0,5

Задание 13 #698

Уровень задания: Сложнее ЕГЭ

Прямые \(y = kx - 3\) и \(y = x - 7\pi\) образуют с положительным направлением оси \(Ox\) углы \(\alpha\) и \(\beta\) соответственно, при этом, \(\cos \alpha = \dfrac{2}{\sqrt{13}}\). Найдите наибольшее из чисел \(k\) и \(\mathrm{tg}\, \beta\).

Показать решение

Таким образом, \(\mathrm{tg}\, \beta = 1\), \(k = \mathrm{tg}\, \alpha = \dfrac{\sin \alpha}{\cos \alpha}\). Из основного тригонометрического тождества находим, что \(\sin \alpha = \pm \dfrac{3}{\sqrt{13}}\), но с учётом \(0 \leq \alpha < \pi\) получаем, что \(\sin \alpha = \dfrac{3}{\sqrt{13}}\).

В итоге \(k = \dfrac{\sin \alpha}{\cos \alpha} = \dfrac{3}{\sqrt{13}} : \dfrac{2}{\sqrt{13}} = 1,5\), а \(\mathrm{tg}\, \beta = 1 < 1,5 = k\), то есть большее из чисел \(k\) и \(\mathrm{tg}\, \beta\) равно \(1,5\).

Ответ: 1,5

Задание 14 #697

Уровень задания: Сложнее ЕГЭ

Прямые \(y = k_1x - \sqrt{2}\) и \(y = k_2x + \pi \sqrt{2}\) образуют с положительным направлением оси \(Ox\) углы \(\alpha\) и \(\beta\) соответственно, при этом, \(k_2 = -k_1\), \(\sin \alpha = \dfrac{3}{\sqrt{10}}\). Найдите наибольший из коэффициентов \(k_1\) и \(k_2\).

Показать решение

Таким образом, \(k_1 = \mathrm{tg}\, \alpha = \dfrac{\sin \alpha}{\cos \alpha}\), при том, что \(\sin \alpha = \dfrac{3}{\sqrt{10}}\) и \(0 \leq \alpha < \pi\). Из основного тригонометрического тождества (для всякого \(\alpha\) выполнено \(\sin^2 \alpha + \cos^2 \alpha = 1\)) получаем, что \(\cos^2 \alpha = \dfrac{1}{10}\), тогда \(\cos \alpha = \pm \dfrac{1}{\sqrt{10}}\), откуда либо \(k_1 = \dfrac{3}{\sqrt{10}} : \dfrac{1}{\sqrt{10}} = 3\), либо \(k_1 = \dfrac{3}{\sqrt{10}} : \left(-\dfrac{1}{\sqrt{10}}\right) = -3\).

При условии \(k_2 = -k_1\) наибольший из коэффициентов \(k_1\) и \(k_2\) равен \(|k_1|\). При \(k_1 = 3\) и при \(k_1 = -3\) получаем \(|k_1| = 3\), тогда наибольший из коэффициентов \(k_1\) и \(k_2\) равен \(3\).

Ответ: 3

1 2 3