Важные аксиомы стереометрии
1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
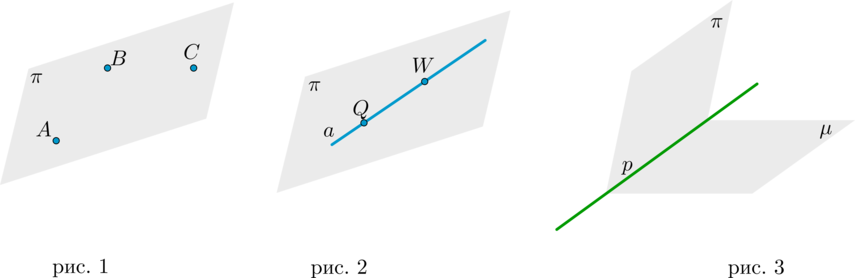
Таким образом, любая плоскость однозначно задается тремя точками, не лежащими на одной прямой: \(\pi=(ABC)\)(рис. 1).
2. Если две точки прямой лежат в некоторой плоскости, то и вся прямая лежит в этой плоскости: \(a\in \pi\).
Говорят также, что плоскость содержит прямую: \(\pi\subset a\) (рис. 2).
3. Если две плоскости имеют общую точку, то они имеют и общую прямую, на которой лежат все общие точки этих плоскостей.
Таким образом, если плоскости пересекаются, то они пересекаются по прямой: \(\pi\cap \mu=p\).
Данная прямая \(p\) называется линией пересечения плоскостей (рис. 3).
Заметим, что плоскость обычно изображают в виде внутренности параллелограмма. Почему? Посмотрите, например, сбоку на стол. В виде какой фигуры выглядит столешница?
Следствия из аксиом
1. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна (рис. 4).
2. Через две пересекающиеся прямые проходит плоскость, и притом только одна (рис. 5).

Доказательство
1. Действительно, отметим на прямой \(a\) некоторые две точки \(A\) и \(B\). Тогда мы получим три точки \(A, B, C\), не лежащие на одной прямой. Через них можно провести единственную плоскость \(\pi\). А т.к. две выбранные точки \(A\) и \(B\) прямой лежат в этой плоскости, то и вся прямая лежит в этой плоскости.
2. Действительно, пусть \(O\) – точка пересечения данных прямых \(p\) и \(q\). Отметим еще по одной точке \(P\) и \(Q\) на каждой прямой (отличающиеся от точки \(O\)). Получили три точки \(P, Q, O\), не лежащие на одной прямой. Через них проходит единственная плоскость \(\pi\). А т.к. две точки каждой прямой лежат в этой плоскости, то и все точки каждой прямой будут лежать в этой плоскости.
\[{\Large{\text{Параллельность в пространстве}}}\]
Определения
Две прямые в пространстве параллельны, если они лежат в одной плоскости и не пересекаются.
Следствие 1
Через две параллельные прямые проходит плоскость, и притом только одна.
Теорема 1
Через любую точку \(A\) в пространстве, не лежащую на данной прямой \(b\), проходит прямая \(a\), параллельная данной, и притом только одна.
Доказательство
Через точку \(A\) и прямую \(b\) можно провести единственную плоскость (по аксиоме); пусть эта плоскость называется \(\pi\). Прямая \(a\), параллельная прямой \(b\), должна лежать с ней в одной плоскости, а также должна проходить через точку \(A\), следовательно, должна лежать в плоскости \(\pi\). Но в плоскости через точку, не лежащую на прямой, можно провести ровно одну прямую, параллельную данной (теорема планиметрии), чтд.
Теорема 2
Если одна из двух параллельных прямых пересекает плоскость, то и другая прямая пересекает эту плоскость.
Доказательство
Пусть \(a\parallel b\) и \(a\cap \pi=A\). Докажем, что и \(b\) пересечет плоскость \(\pi\) (назовем их точку пересечения \(B\)).
Проведем через прямые \(a\) и \(b\) плоскость \(\mu\) (это возможно в силу определения параллельных прямых). Тогда плоскости \(\pi\) и \(\mu\) имеют общую точку \(A\), следовательно, имеют и общую прямую \(p\), на которой лежат все их общие точки. Но т.к. \(b\parallel a\) и \(a\cap
p=A\), то прямая \(b\) тоже пересекает прямую \(p\). Значит, прямая \(b\) пересекает и плоскость \(\mu\) (это и есть точка \(B\)).
Теорема 3: о параллельности трех прямых
Если прямая \(a\) параллельна прямой \(b\), а та в свою очередь параллельна прямой \(c\), то \(a\parallel c\).
Доказательство
1) Отметим некоторую точку \(C\) на прямой \(c\) и проведем плоскость \(\pi\) через прямую \(a\) и точку \(C\). Прямая \(c\) будет лежать в этой плоскости. Действительно, т.к. прямая \(c\) и плоскость \(\pi\) имеют общую точку \(C\), то в противном случае прямая \(c\) будет пересекать эту плоскость. Но т.к. \(b\parallel c\), то и прямая \(b\) будет пересекать \(\pi\); а т.к. \(a\parallel b\), то и прямая \(a\) будет пересекать эту плоскость. А это противоречит нашему построению.
2) Теперь прямые \(a\) и \(c\) лежат в одной плоскости, значит, они могут либо пересекаться, либо быть параллельны. Предположим, что \(c\) пересекает \(a\) в точке \(A\). Тогда получается, что через точку \(A\) проведены две прямые, параллельные прямой \(b\), что противоречит теореме 1.
Определение
Существует три вида взаимного расположения прямой и плоскости:
1. прямая имеет с плоскостью две общие точки (то есть лежит в плоскости) — рис. 4;
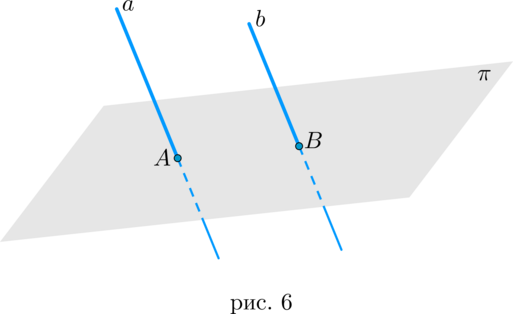
2. прямая имеет с плоскостью ровно одну общую точку (то есть пересекает плоскость) — рис. 6;
3. прямая не имеет с плоскостью общих точек (то есть параллельна плоскости).
Теорема 4: признак параллельности прямой и плоскости
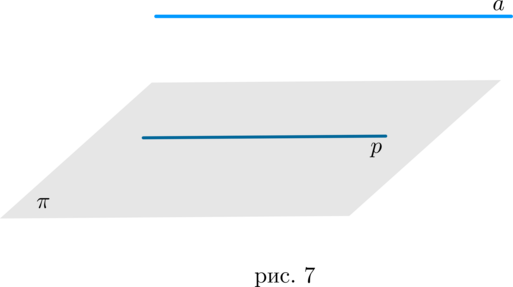
Если прямая \(a\), не лежащая в плоскости \(\pi\), параллельна некоторой прямой \(p\), лежащей в плоскости \(\pi\), то она параллельна данной плоскости (рис. 7).
Доказательство
Докажем, что прямая \(a\) не может пересекать плоскость \(\pi\) (случай, что прямая лежит в плоскости, невозможен по условию). Предположим, что это не так. Во-первых, проведем плоскость \(\mu\) через прямые \(a\) и \(p\) (значит, плоскости \(\pi\) и \(\mu\) пересекаются по прямой \(p\)). Во-вторых, пусть \(a\cap\pi=A\). Т.к. \(a\parallel p\), то точка \(A\) не может лежать на прямой \(p\). Значит, плоскости \(\pi\) и \(\mu\) имеют еще одну общую точку \(A\), не лежащую на их линии пересечения, что противоречит аксиоме 3. Чтд.
Следствие 2
Пусть прямая \(p\) параллельна плоскости \(\mu\). Если плоскость \(\pi\) проходит через прямую \(p\) и пересекает плоскость \(\mu\), то линия пересечения плоскостей \(\pi\) и \(\mu\) — прямая \(m\) — параллельна прямой \(p\) (рис. 8).
Доказательство
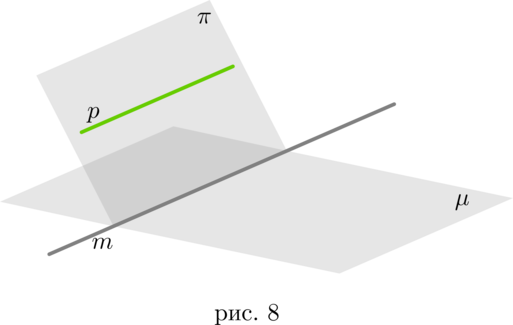
Т.к. прямые \(m\) и \(p\) лежат в одной плоскости \(\pi\), то они могут быть либо параллельны, либо пересекаться, либо совпадать. Совпадать они не могут, потому что тогда \(p\in \mu\), а это противоречит условию. Если \(m\cap p=O\), то \(p\) пересекает плоскость \(\mu\) в точке \(O\), что опять же противоречит условию. Значит, \(m\parallel p\).
Следствие 3
Если прямые \(a\) и \(b\) параллельны и прямая \(a\) также параллельна плоскости \(\alpha\), то и прямая \(b\) либо параллельна, либо лежит в плоскости \(\alpha\).
Определение
Существует три типа взаимного расположения плоскостей в пространстве: совпадают (имеют три общие точки, не лежащие на одной прямой), пересекаются (имеют общие точки, лежащие строго на одной прямой), и не имеют общих точек.
Если две плоскости не имеют общих точек, то они называются параллельными плоскостями.
Теорема 5: признак параллельности плоскостей
Если две пересекающиеся прямых из одной плоскости параллельны двум пересекающимся прямым из другой плоскости, то такие плоскости будут параллельны.
Доказательство
Рассмотрим две плоскости \(\pi\) и \(\mu\) и в них пересекающиеся прямые \(a, b\) и \(a_1, b_1\) соответственно, такие что \(a\parallel a_1, \
b\parallel b_1\). Докажем, что плоскости не имеют общих точек.
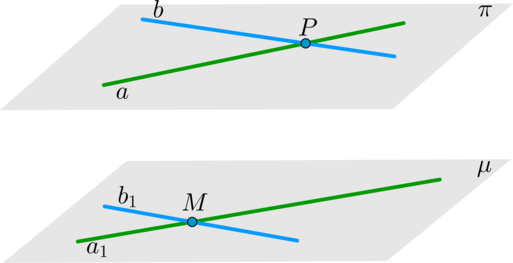
Предположим, что это не так. Пусть плоскости имеют общую точку, значит они имеют и общую прямую \(y\): \(\pi\cap \mu=y\). Данная прямая не может быть параллельна обеим прямым \(a\) и \(b\) (т.к. они все лежат в одной плоскости \(\pi\)), значит, хотя бы одну из этих прямых она пересекает. Пусть это будет прямая \(a\), то есть \(a\cap y=Y\). Т.к. прямая \(y\) лежит и в плоскости \(\mu\), то \(Y\in \mu\), то есть прямая \(a\) имеет с плоскостью \(\mu\) общую точку \(Y\). Но это невозможно, т.к. по признаку параллельности прямой и плоскости прямая \(a\) параллельна плоскости \(\mu\). Чтд.
Следствие 4
Если две параллельные плоскости \(\alpha\) и \(\beta\) пересечены третьей плоскостью \(\gamma\), то линии пересечения плоскостей также параллельны:
\[\alpha\parallel \beta, \ \alpha\cap \gamma=a, \ \beta\cap\gamma=b \Longrightarrow a\parallel b\]

Следствие 5
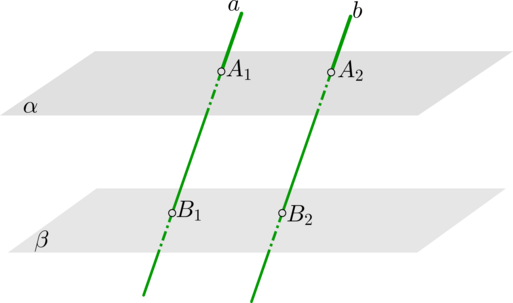
Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны:
\[\alpha\parallel \beta, \ a\parallel b \Longrightarrow
A_1B_1=A_2B_2\]