Определение
Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.
Теорема (первый признак параллелограмма)
Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм.
Доказательство
Пусть в четырехугольнике \(ABCD\) стороны \(AB\) и \(CD\) параллельны и \(AB = CD\).

Проведём диагональ \(AC\), разделяющую данный четырехугольник на два равных треугольника: \(ABC\) и \(CDA\). Эти треугольники равны по двум сторонам и углу между ними (\(AC\) – общая сторона, \(AB = CD\) по условию, \(\angle 1 = \angle 2\) как накрест лежащие углы при пересечении параллельных прямых \(AB\) и \(CD\) секущей \(AC\)), поэтому \(\angle 3 = \angle 4\). Но углы \(3\) и \(4\) накрест лежащие при пересечении прямых \(AD\) и \(BC\) секущей \(AC\), следовательно, \(AD\parallel BC\). Таким образом, в четырехугольнике \(ABCD\) противоположные стороны попарно параллельны, и, значит, четырехугольник \(ABCD\) – параллелограмм.
Теорема (второй признак параллелограмма)
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.
Доказательство
Проведём диагональ \(AC\) данного четырехугольника \(ABCD\), разделяющую его на треугольники \(ABC\) и \(CDA\).

Эти треугольники равны по трем сторонам (\(AC\) – общая, \(AB = CD\) и \(BC = DA\) по условию), поэтому \(\angle 1 = \angle 2\) – накрест лежащие при \(AB\) и \(CD\) и секущей \(AC\). Отсюда следует, что \(AB\parallel CD\). Так как \(AB = CD\) и \(AB\parallel CD\), то по первому признаку параллелограмма четырёхугольник \(ABCD\) – параллелограмм.
Теорема (третий признак параллелограмма)
Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.
Доказательство
Рассмотрим четырехугольник \(ABCD\), в котором диагонали \(AC\) и \(BD\) пересекаются в точке \(O\) и делятся этой точкой пополам.
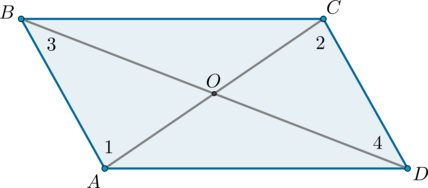
Треугольники \(AOB\) и \(COD\) равны по первому признаку равенства треугольников (\(AO = OC\), \(BO = OD\) по условию, \(\angle AOB = \angle
COD\) как вертикальные углы), поэтому \(AB = CD\) и \(\angle 1 = \angle
2\). Из равенства углов \(1\) и \(2\) (накрест лежащие при \(AB\) и \(CD\) и секущей \(AC\)) следует, что \(AB\parallel CD\).
Итак, в четырехугольнике \(ABCD\) стороны \(AB\) и \(CD\) равны и параллельны, значит, по первому признаку параллелограмма четырехугольник \(ABCD\) – параллелограмм.
Свойства параллелограмма:
1. В параллелограмме противоположные стороны равны и противоположные углы равны.
2. Диагонали параллелограмма точкой пересечения делятся пополам.
Свойства биссектрисы параллелограмма:
1. Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
2. Биссектрисы смежных углов параллелограмма пересекаются под прямым углом.
3. Отрезки биссектрис противоположных углов равны и параллельны.
Доказательство
1) Пусть \(ABCD\) – параллелограмм, \(AE\) – биссектриса угла \(BAD\).
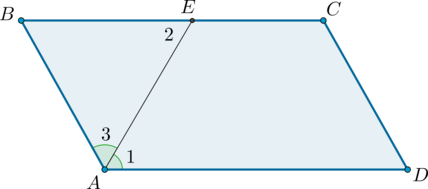
Углы \(1\) и \(2\) равны как накрест лежащие при параллельных прямых \(AD\) и \(BC\) и секущей \(AE\). Углы \(1\) и \(3\) равны, так как \(AE\) – биссектриса. В итоге \(\angle 3 = \angle 1 = \angle 2\), откуда следует, что треугольник \(ABE\) – равнобедренный.
2) Пусть \(ABCD\) – параллелограмм, \(AN\) и \(BM\)– биссектрисы углов \(BAD\) и \(ABC\) соответственно.
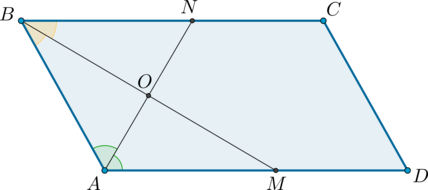
Так как сумма односторонних углов при параллельных прямых и секущей равна \(180^{\circ}\), тогда \(\angle DAB + \angle ABC =
180^{\circ}\).
Так как \(AN\) и \(BM\) – биссектрисы, то \(\angle BAN + \angle ABM =
0,5(\angle DAB + \angle ABC) = 0,5\cdot 180^\circ = 90^{\circ}\), откуда \(\angle AOB = 180^\circ - (\angle BAN + \angle ABM) =
90^\circ\).
3. Пусть \(AN\) и \(CM\) – биссектрисы углов параллелограмма \(ABCD\).
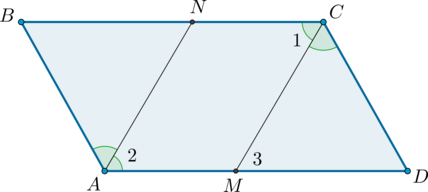
Так как в параллелограмме противоположные углы равны, то \(\angle 2 =
0,5\cdot\angle BAD = 0,5\cdot\angle BCD = \angle 1\). Кроме того, углы \(1\) и \(3\) равны как накрест лежащие при параллельных прямых \(AD\) и \(BC\) и секущей \(CM\), тогда \(\angle 2 = \angle 3\), откуда следует, что \(AN\parallel CM\). Кроме того, \(AM\parallel CN\), тогда \(ANCM\) – параллелограмм, следовательно, \(AN = CM\).








