\(\blacktriangleright\) На ОДЗ верны следующие формулы:
\[\large{\begin{array}{|lcl|}
\hline \log_a1=0& \qquad & \log_aa=1\\
&&\\
\log_{a^n}{b^m}=\frac mn\log_{|a|}{|b|}&& a^{\log_bc}=c^{\log_ba}\\
&&\\
\log_a{bc}=\log_a{|b|}+\log_a{|c|}&& \log_a{\dfrac bc}=\log_a{|b|}-\log_a{|c|}\\
&&\\
\log_ab\cdot \log_bc=\log_ac & \Longleftrightarrow & \log_bc=\dfrac{\log_ac}{\log_ab}\\
&&\\
\log_ab\cdot \log_ba=1 & \Longleftrightarrow & \log_ab=\dfrac1{\log_ba}\\
&&\\
\hline
\end{array}}\]
\(\blacktriangleright\) Стандартное логарифмическое неравенство \[{\Large{\log_a{h(x)}\geqslant \log_a{g(x)} \quad
(*)}}\] где \(a>0,\ a\ne 1\)
(на месте знака \(\geqslant\) может стоять любой из знаков \(\leqslant,\
>,\ <\))
Логарифмическая функция \(f(x)=\log_ax\) является возрастающей, если число \(a>1\), и убывающей, если \(0<a<1\), и определена при всех положительных \(x\) (то есть ее область определения \(x\in (0;+\infty)\)).
На графике приведен пример возрастающей логарифмической функции \(f_1(x)=\log_2x\) и убывающей логарифмической функции \(f_2(x)=\log_{\,0,5}x\).
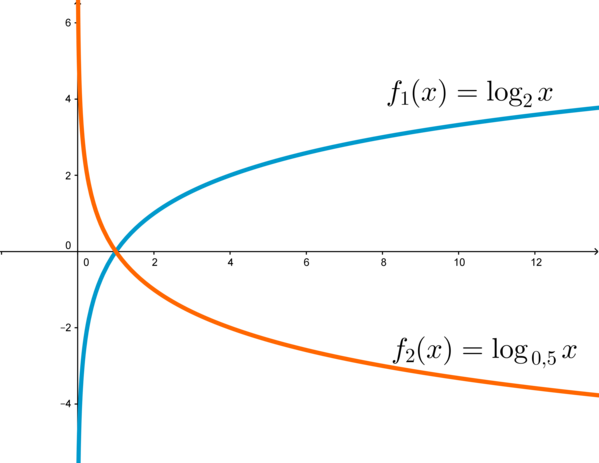
Напомним, что функция возрастает, если при увеличении \(x\) увеличивается и \(f(x)\). Функция убывает, если при увеличении \(x\) уменьшается \(f(x)\).
Таким образом, неравенство \((*)\) есть не что иное, как сравнение \(f(h)\) и \(f(g)\). Если функция \(f\) — возрастает, то неравенство \(f(h)\geqslant f(g)\) равносильно неравенству \(h\geqslant g\), а если убывает — то неравенству \(h\leqslant g\).
Поэтому для того, чтобы решить неравенство \((*)\), нужно сравнить основание \(a\) с единицей:
если \({\large{a>1}}\), то данное неравенство равносильно системе (не забываем про ОДЗ!) \[{\Large{\begin{cases} h(x)\geqslant g(x)\\ g(x)>0 \end{cases}}}\] Заметим, что условие \(h(x)>0\) учитывается автоматически в такой системе, т.к. если \(h\geqslant g\), а \(g>0\), то и \(h>0\).
если \({\large{0<a<1}}\), то данное неравенство равносильно системе \[{\Large{\begin{cases} h(x)\leqslant g(x)\\ h(x)>0 \end{cases}}}\]
Заметим, что условие \(g(x)>0\) учитывается автоматически в такой системе.
\(\blacktriangleright\) Напомним, что область значений логарифмической функции — все числа, т.е. \(\log_ax\in \mathbb{R}\) при всех возможных \(a\) и \(x\).
\(\blacktriangleright\) С помощью формулы \({\Large {b=\log_a{a^b}}}\) можно любое число \(b\) представить в виде логарифма по необходимому основанию \(a>0,\ a\ne 1\).
Пример 1. Решить неравенство \(\log_2 {(x^2+7)}>4\)
Представим по формуле \(4=\log_2{2^4}=\log_2{16}\), тогда неравенство примет вид \[\log_2{(x^2+7)}>\log_2 {16} \Leftrightarrow
\begin{cases} x^2+7>16\\ x^2+7>0 \end{cases}\] (знак неравенства не сменится, т.к. основание логарифмов \(2>1\)).
Второе неравенство \(x^2+7>0\) (это и есть ОДЗ) выполнено при всех \(x\).
Первое неравенство системы равносильно \(x^2-9>0 \Leftrightarrow
(x-3)(x+3)>0 \Rightarrow x\in (-\infty;-3)\cup(3;+\infty)\).
Таким образом, после пересечения решений обоих неравенств системы решением исходного неравенства будут \(x\in
(-\infty;-3)\cup(3;+\infty)\).
\(\blacktriangleright\) Рассмотрим неравенства вида \[{\Large{\log_{h(x)}{f(x)}\geqslant \log_{h(x)}{g(x)}}}\] (на месте знака \(\geqslant\) может стоять любой из знаков \(\leqslant,\
>,\ <\))
То есть когда в основании логарифма находится не конкретное число, а функция, зависящая от \(x\).
Данное неравенство равносильно совокупности: \[{\Large{\left[\begin{gathered}
\begin{aligned}
&\begin{cases}
h(x)>1\\
f(x)\geqslant g(x)\\
g(x)>0
\end{cases}\\[4pt]
&\begin{cases}
0<h(x)<1\\
f(x)\leqslant g(x)\\
f(x)>0
\end{cases}
\end{aligned}
\end{gathered}
\right.}}\]
Иногда удобно выписать ОДЗ отдельно. Тогда неравенство будет равносильно системе: \[{\Large{\begin{cases}
f(x)>0 \quad (\textbf{ОДЗ})\\
g(x)>0 \quad (\textbf{ОДЗ})\\[3pt]
\left[\begin{gathered}
\begin{aligned}
&\begin{cases}
h(x)>1\\
f(x)\geqslant g(x)
\end{cases}\\[3pt]
&\begin{cases}
0<h(x)<1\\
f(x)\leqslant g(x)
\end{cases}
\end{aligned}
\end{gathered}
\right.
\end{cases}}}\]
Пример 2. Решить неравенство \(\log_x{(3x-1)}>1\)
Данное неравенство равносильно:
\(\log_x{(3x-1)}>\log_xx \ \Leftrightarrow \ \left[
\begin{gathered}
\begin{aligned}
&\begin{cases}
x>1\\
3x-1> x\\
x>0
\end{cases}\\
&\begin{cases}
0<x<1\\
3x-1< x\\
3x-1>0
\end{cases}
\end{aligned}
\end{gathered}
\right. \ \Leftrightarrow \ \left[
\begin{gathered}
\begin{aligned}
&x>1\\
&\dfrac13<x<\dfrac12
\end{aligned}
\end{gathered}
\right. \ \Leftrightarrow \quad x\in
\left(\dfrac13;\dfrac12\right)\cup\Big(1;+\infty\Big)\)
Пример 3. Решить неравенство \(\log_{x^2}{(x+1)^2}\leq 1\)
Выпишем ОДЗ для аргумента логарифма: \((x+1)^2>0 \Rightarrow
x\ne -1\).
Для основания логарифма ОДЗ отдельно выписывать не имеет смысла, т.к. мы будем учитывать его в самом решении: рассматривать случаи, когда основание больше \(1\) и когда оно находится между \(0\) и \(1\).
Таким образом, на ОДЗ неравенство равносильно совокупности (учитывая, что \(1=\log_{x^2}{x^2}\)) \[\left[
\begin{gathered}
\begin{aligned}
&\begin{cases}
x^2>1\\
(x+1)^2\leqslant x^2
\end{cases}\\[2pt]
&\begin{cases}
0<x^2<1\\
(x+1)^2\geqslant x^2
\end{cases}
\end{aligned}
\end{gathered}
\right. \quad \Leftrightarrow \quad \left[
\begin{gathered}
\begin{aligned}
&\begin{cases}
x^2-1>0\\
(x+1)^2-x^2\leqslant 0
\end{cases}\\[2pt]
&\begin{cases}
x^2<1\\
x^2>0\\
(x+1)^2- x^2\geqslant 0
\end{cases}
\end{aligned}
\end{gathered}
\right.\quad \Leftrightarrow \quad \left[
\begin{gathered}
\begin{aligned}
&\begin{cases}
(x-1)(x+1)>0\\
(x+1-x)(x+1+x)\leqslant 0
\end{cases}\\[2pt]
&\begin{cases}
(x-1)(x+1)<0\\
x\ne 0\\
(x+1-x)(x+1+x)\geqslant 0
\end{cases}
\end{aligned}
\end{gathered}
\right.\quad \Leftrightarrow \quad\]
\[\quad \Leftrightarrow \quad
\left[
\begin{gathered}
\begin{aligned}
&\begin{cases}
x\in (-\infty;-1)\cup(1;+\infty)\\
x\in (-\infty;-\dfrac12\big]
\end{cases}\\[2pt]
&\begin{cases}
x\in (-1;1)\\
x\ne 0\\
x\in\big[-\dfrac12;+\infty)
\end{cases}
\end{aligned}
\end{gathered}
\right. \quad \Leftrightarrow \quad x\in
\Big(-\infty;-1\Big)\cup\Big[-\dfrac12;0\Big)\cup\Big(0;1\Big)\]
Пересекая данный ответ с ОДЗ (\(x\ne -1\)), получим тот же ответ.
\(\blacktriangleright\) Таким образом, как правило, для того, чтобы система (совокупность) не выглядела слишком огромной, удобно записывать ОДЗ неравенства отдельно, а затем просто пересекать решение системы (совокупности) с этим ОДЗ. Что мы и сделали в примере \(3\).




