Уровень составитель ЕГЭ. Тренировочный вариант №3

Билет со скидкой стоит \(500 \cdot (1 - 0,01) = 495\) рублей. Из группы в пять человек двое шли со скидкой, остальные трое платили по \(500\) рублей за билет. В сумме эти \(5\) киноманов отдали \(500 \cdot 3 + 495 \cdot 2 = 2490\) рублей.

Ответ: 2490

По рисунку видно, что в указанный период времени наименьшая температура составляла \(20\) градусов Фаренгейта.

Ответ: 20

Рассмотрим треугольники \(CAB\) и \(CED\):
\(\angle C\) – общий,
\[\dfrac{CA}{CE} = \dfrac{AE + CE}{CE} = \dfrac{AE}{CE} + 1 = \dfrac{1}{3} + 1 = \dfrac{4}{3} = \dfrac{CB}{CD},\] тогда треугольники \(CAB\) и \(CED\) подобны по пропорциональности двух сторон и равенству углов между ними.

В подобных треугольниках против пропорциональных сторон лежат равные углы, тогда \(\angle CED = \angle CAB\), откуда \(\angle CED - \angle CAB = 0^{\circ}\).

Ответ: 0

Так как вероятности выпадения любой упорядоченной пары чисел вида \((a; b)\) одинаковы (\(a\) и \(b\) – числа из множества \(1\), \(2\), \(3\), \(4\), \(5\), \(6\)), то искомая вероятность есть просто отношение суммарного количества пар \((a; b)\) таких, что \(a + b\) кратно \(4\), к общему количеству пар вида \((a; b)\). Сумма \(a + b\) кратна 4 в тех случаях, когда \(a + b = 4\) или \(a + b = 8\), или \(a + b = 12\).

Под условие \(a + b = 4\) подходят \(3\) пары: \((1; 3)\), \((3; 1)\) и \((2; 2)\),
под условие \(a + b = 8\) подходят \(5\) пар: \((2; 6)\), \((6; 2)\), \((3; 5)\), \((5; 3)\), \((4; 4)\),
под условие \(a + b = 12\) подходит \(1\) пара: \((6; 6)\),
общее количество возможных пар вида \((a; b)\) равно \(36\).

Итого: искомая вероятность равна \[\dfrac{3 + 5 + 1}{36} = 0,25.\] После округления до сотых получаем \(0,25\).

Ответ: 0,25

ОДЗ: \(x \neq -\dfrac{2}{3}\). Решим на ОДЗ:

Перенесём всё влево и приведём к общему знаменателю: \[\dfrac{1 - 2x - x\cdot\left(\dfrac{2}{3} + x\right)}{\dfrac{2}{3} + x} = 0.\] Дробь равна нулю в том и только том случае, когда её числитель равен нулю, а знаменатель отличен от нуля, тогда \[1 - 2x - x\cdot\left(\dfrac{2}{3} + x\right) = 0\qquad\Leftrightarrow\qquad x^2 + 2\dfrac{2}{3}x - 1 = 0.\] Дискриминант данного уравнения \[D = \dfrac{64}{9} + 4 = \left(\dfrac{10}{3}\right)^2.\] Корни квадратного уравнения \[x_1 = \dfrac{1}{3}, \ x_2 = -3\] – подходят по ОДЗ. Ответ: \(x = -3\) – наименьший корень.

Ответ: -3

Построим отрезки \(CA\), \(AD\) и \(CB\), точку пересечения \(CD\) и \(AB\) обозначим \(E\).



\(\angle BCD = \angle BAD\) как вписанные, опирающиеся на общую дугу. Так как \(AB\) – диаметр, то \(\angle BCA = 90^{\circ}\).

Тогда \(\angle BCD\) дополняет \(\angle DCA\) до \(90^{\circ}\), а \(\angle BAD\) дополняет \(\angle CDA\) до \(90^{\circ}\) и из равенства \(\angle BCD = \angle BAD\) вытекает \(\angle DCA = \angle CDA\), следовательно, дуги \(AC\) и \(AD\) равны.

Ответ: 0

Для функции \(f(x)\), у которой производная в точке \(x_0\) имеет смысл, \(f'(x_0) < 0\) равносильно тому, что \(f(x)\) убывает в \(x_0\).

На интервале \((-0,5; 4,3)\) целыми являются точки \(0\), \(1\), \(2\), \(3\), \(4\). Среди этих точек \(f(x)\) убывает только в \(0\), \(2\) и \(3\). Таким образом, производная функции \(y = f(x)\) отрицательна в \(3\) целых точках.

Ответ: 3

Так как \(AD\) и \(BC\) – высоты цилиндра, то \(ABCD\) – прямоугольник, тогда \[S_{ABCD} = AD\cdot DC = H\cdot R = \dfrac{16\sqrt{3}}{\sqrt[3]{\pi^2}}.\]

Рассмотрим прямоугольный треугольник \(ADC\):
Т.к. \(\angle DAC = 60^\circ\), то \[AD = \mathrm{tg}\, \angle ACD\cdot DC = \mathrm{tg}\, 30^\circ\cdot R = \dfrac{R}{\sqrt{3}},\] т.е. \(H = \dfrac{R}{\sqrt{3}}\) или \(R = \sqrt{3}H\).

Подставляя выражение для \(R\) в \(S_{ABCD}\), получим: \[H^2\cdot\sqrt{3} = \dfrac{16\sqrt{3}}{\sqrt[3]{\pi^2}},\] откуда \(H = \dfrac{4}{\sqrt[3]{\pi}}\), тогда \(R = \dfrac{4\sqrt{3}}{\sqrt[3]{\pi}}\).

\[V_{\text{цил}} = \pi R^2 H = \pi\cdot \dfrac{16\cdot 3}{\sqrt[3]{\pi^2}}\cdot\dfrac{4}{\sqrt[3]{\pi}} = 192.\]

Ответ: 192

По свойствам логарифма при \(\dfrac{x^2}{y^3} > 0\), \(1 \neq x^2 > 0\): \[\log_{x^2}\left(\dfrac{x^2}{y^3}\right) = \log_{x^2}(x^2) - \log_{x^2}(y^3) = 1 - \dfrac{1}{2} \cdot 3 \log_{x}y.\]

\(\log_{x}y = \dfrac{1}{\log_{y}x} = 0,1\) и значит окончательно \(\log_{x^2}\left(\dfrac{x^2}{y^3}\right) = 1 - 1,5 \cdot 0,1 = 1 - 0,15 = 0,85\).

Ответ: 0,85

Пусть длина ребра начального куба равна \(x\, м\), тогда объем ограниченного им тела равен \(x^3\, м^3\), следовательно, начальная сила Архимеда равна \(F_{A_{\text{н}}} = \rho gx^3\). Обозначим ребро искомого куба за \(y\). Так как сила Архимеда должна увеличиться не менее, чем в \(64\) раза, то \[\rho gy^3 \geqslant 64F_{A_{\text{н}}} = 64\rho gx^3\qquad\Leftrightarrow\qquad y^3 - 64x^3\geqslant 0\qquad\Leftrightarrow\qquad y^3 - (4x)^3 \geqslant 0.\] Так как фактически в задаче просят найти именно отношение \(y\) к \(x\), то обозначим \(\dfrac{y}{x} = z\), откуда \(y = zx\), следовательно, \[(zx)^3 - (4x)^3 \geqslant 0.\] Последнее неравенство можно разделить на \(x^3\) с учётом того, что \(x^3 > 0\) (так как \(x > 0\)). В результате получим \[z^3 - 4^3\geqslant 0.\] Решим это неравенство методом интервалов. Найдём корни уравнения \(z^3 - 4^3 = 0\): \(z = 4\), тогда:



то есть минимальное число раз, в которое надо увеличить ребро куба, ограничивающего тело, чтобы сила Архимеда, действующая на тело, увеличилась не менее, чем в \(64\) раза, равно \(4\).

Ответ: 4

Пусть \(S\, км\) – расстояние, которое проплыл теплоход по пути из А в В, тогда

\(\dfrac{S}{12 + 2}\) часов – время, которое теплоход плыл по течению,

\(\dfrac{S}{12 - 2}\) часов – время, которое теплоход плыл против течения,

плыл теплоход всего \(29 - 5 = 24\) часа, тогда:

\[\dfrac{S}{14} + \dfrac{S}{10} = 24,\] откуда находим \(S = 140\, км\).

Ответ: 140

1) \[y' = e^{x^2 - 2016x + 2017}\cdot(2x - 2016).\]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна \(0\) или не существует): \[e^{x^2 - 2016x + 2017}\cdot(2x - 2016) = 0\qquad\Leftrightarrow\qquad x - 2016 = 0\] (так как \(e^t > 0\) при любом \(t\)), откуда находим \(x = 1008\). Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.

2) Найдём промежутки знакопостоянства \(y'\):



3) Эскиз графика \(y\):



Таким образом, \(x = 1008\) – точка минимума функции \(y\).

Ответ: 1008

ОДЗ: \(x\) – произвольное. Решим на ОДЗ:

а) Перенесём всё влево:

\[\begin{aligned} 2\cos^2 (2x) - 3\sqrt{3}\cos (2x) + 3 = 0. \end{aligned}\]

Полученное уравнение представляет собой квадратное уравнение относительно \(\cos (2x)\).

Сделаем замену \(\cos (2x) = t\), тогда уравнение примет вид \[2t^2 - 3\sqrt{3}t + 3 = 0.\] Его дискриминант \(D = 27 - 24 = 3\), тогда \(t_{1, 2} = \dfrac{3\sqrt{3}\pm\sqrt{3}}{4}\), откуда \(t_1 = \sqrt{3}\), \(t_2 = \dfrac{\sqrt{3}}{2}\), следовательно,
\(\cos (2x) = \sqrt{3}\) или \(\cos (2x) = \dfrac{\sqrt{3}}{2}\).

Так как \(\cos (2x)\leqslant 1\), то \(\cos (2x) = \sqrt{3}\) быть не может, следовательно, \(\cos (2x) = \dfrac{\sqrt{3}}{2}\).

Уравнение \(\cos y = a\) имеет решения \(y = \pm\mathrm{arccos}\, a + 2\pi k\), где \(k\in\mathbb{Z}\), следовательно,   уравнение \(\cos (2x) = \dfrac{\sqrt{3}}{2}\) имеет решения, для которых выполнено \(2x = \pm\dfrac{\pi}{6} + 2\pi k\), где \(k\in\mathbb{Z}\), тогда \[x = \pm\dfrac{\pi}{12} + \pi k, k\in\mathbb{Z}.\]

б) \[-\pi < \dfrac{\pi}{12} + \pi k \leqslant \pi\qquad\Leftrightarrow\qquad -\dfrac{13\pi}{12} < \pi k \leqslant \dfrac{11\pi}{12}\qquad\Leftrightarrow\qquad -\dfrac{13}{12} < k \leqslant \dfrac{11}{12},\] но \(k\in\mathbb{Z}\), следовательно, среди этих решений подходят решения при \(k = -1\) и \(k = 0\): \(x = -\dfrac{11\pi}{12}\) и \(x = \dfrac{\pi}{12}\).

\[-\pi < -\dfrac{\pi}{12} + \pi k \leqslant \pi\qquad\Leftrightarrow\qquad -\dfrac{11\pi}{12} < \pi k \leqslant \dfrac{13\pi}{12}\qquad\Leftrightarrow\qquad -\dfrac{11}{12} < k \leqslant \dfrac{13}{12},\] но \(k\in\mathbb{Z}\), следовательно, среди этих решений подходят решения при \(k = 0\) и \(k = 1\): \(x = -\dfrac{\pi}{12}\) и \(x = \dfrac{11\pi}{12}\).

Ответ:

а) \(\pm\dfrac{\pi}{12} + \pi k\), где \(k\in\mathbb{Z}\).

б) \(-\dfrac{11\pi}{12}\), \(-\dfrac{\pi}{12}\), \(\dfrac{\pi}{12}\), \(\dfrac{11\pi}{12}\).

а) Построим сечение параллелепипеда плоскостью \(MNK\).
Т.к. \(MN\parallel (ABC), MN\subset(MNK) \Rightarrow \) плоскость \(MNK\) пересечет плоскость \(ABC\) по прямой, параллельной \(MN\) (пусть \(KT\) - линия пересечения плоскостей \(MNK\) и \(ABC\); если \(KT\cap MN\ne \varnothing \Rightarrow MN\cap (ABC)\ne \varnothing \Rightarrow MN\) не может быть параллельна \((ABC)\)).

Пусть \(T\) лежит на \(AD\), значит, \(T\) – середина \(AD\).
Рассмотрим сечение \(BB_1D_1D\). Эта плоскость пересекает \(MN\) и \(KT\) в их серединах. Пусть \(O\) – середина \(MN\), \(Q\) – середина \(KT\). Прямая \(OQ\) пересекает ребро \(BB_1\) в точке \(P\). Прямая \(PM\cap AA_1=R, PN\cap CC_1 = S\), таким образом, \(PSKTR\) – искомое сечение.

б) Без ограничения общности можно считать, что \(AB=BC=1, AA_1=\sqrt2\). Таким образом, \(BD=\sqrt2=BB_1\).

\(QD=\dfrac{1}{4}BD\). Точка \(O\) лежит на отрезке \(LL_1\), где \(L\) – середина \(BB_1\), \(L_1\) – середина \(DD_1\). Найдем \(LO\).
\(ML\perp BB_1C_1C \Rightarrow ML\perp LN \Rightarrow MLN\) – прямоугольный треугольник, причем \(ML=LN=\dfrac{1}{2}, \ MN=\dfrac{1}{2}AC=\dfrac{\sqrt2}{2}\).

\(LO=\dfrac{1}{2}MN=\dfrac{\sqrt2}{4}\) как медиана прямоугольного треугольника, проведенная к гипотенузе. \(\Rightarrow LO=\dfrac{1}{4}LL_1\).

\(\bigtriangleup OO_1Q\) – равнобедренный \(\Rightarrow \bigtriangleup PBQ\) – равнобедренный (т.к. \(\bigtriangleup OO_1Q \sim \bigtriangleup PBQ\)) \(\Rightarrow PB=BQ \Rightarrow B_1P:PB=1:3\).

Ответ:

б) \(1:3\)

ОДЗ:

\[\begin{aligned} &\begin{cases} x^2 + x > 0\\ x^2 + x \neq 1\\ x^2-4x+4 > 0 \end{cases} \ \Leftrightarrow\\ x \in \left(-\infty; -\dfrac{1+\sqrt{5}}{2}\right) \cup \left(-\dfrac{1+\sqrt{5}}{2}; -1\right) &\cup \left(0; \dfrac{-1+\sqrt{5}}{2}\right)\cup \left(\dfrac{-1+\sqrt{5}}{2}; 2\right)\cup \left(2; +\infty\right) \end{aligned}\]

\[2\log_{x^2+x}\sqrt{x^2-4x+4} - \log_{x^2 + x}(x^2 + x)\leqslant 0\quad\Leftrightarrow\quad \log_{x^2+x}\dfrac{x^2-4x + 4}{x^2+x}\leqslant 0.\] По методу рационализации это неравенство на ОДЗ равносильно:

\[\begin{aligned} &(x^2 + x - 1)\left(\dfrac{x^2-4x+4}{x^2+x} - 1\right)\leqslant 0 \ \ \Leftrightarrow\ \ (x^2 + x - 1)\cdot\dfrac{x^2-4x+4 - (x^2 + x)}{x^2+x}\leqslant 0 \ \ \Leftrightarrow\\ &\Leftrightarrow\ \ (x^2 + x - 1)\cdot\dfrac{-5x+4}{x^2+x}\leqslant 0\ \ \Leftrightarrow\ \ (x^2 + x - 1)\cdot\dfrac{5x - 4}{x^2+x}\geqslant 0 \end{aligned}\]

По методу интервалов:



откуда \(x \in\left[-\dfrac{1+\sqrt{5}}{2}; -1\right)\cup\left(0; \dfrac{-1+\sqrt{5}}{2}\right]\cup[0,8; +\infty)\).
Пересечем ответ с ОДЗ: \(x \in\left(-\dfrac{1+\sqrt{5}}{2}; -1\right) \cup \left(0; \dfrac{-1+\sqrt{5}}{2}\right)\cup \left[0,8; 2\right)\cup \left(2; +\infty\right)\).
Окончательный ответ \[x \in \left(-\dfrac{1+\sqrt{5}}{2}; -1\right) \cup \left(0; \dfrac{-1+\sqrt{5}}{2}\right)\cup \left[0,8; 2\right)\cup \left(2; +\infty\right)\,.\]

Ответ:

\(\left(-\dfrac{1+\sqrt{5}}{2}; -1\right) \cup \left(0; \dfrac{-1+\sqrt{5}}{2}\right)\cup \left[0,8; 2\right)\cup \left(2; +\infty\right)\)

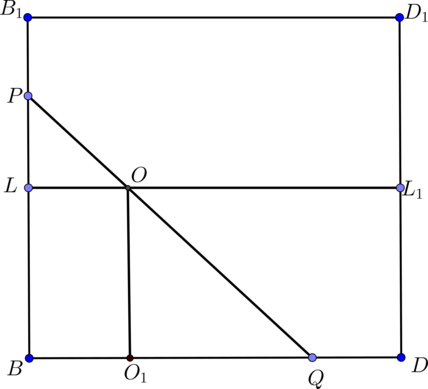
а) Рассмотрим треугольники \(APS\) и \(PBQ\): \(\angle BQP = 90^\circ = \angle PAS\). Так как \(\angle SPQ = 90^\circ\), то \(\angle APS + \angle BPQ = 90^\circ\), откуда \(\angle APS = \angle PBQ\), следовательно, треугольники \(APS\) и \(PBQ\) подобны по двум углам.

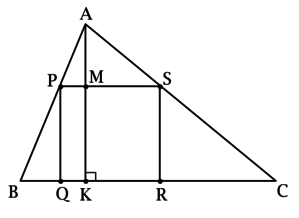
Из подобия этих треугольников получаем: \[\dfrac{PS}{BP} = \dfrac{AS}{PQ},\] но \(PS = PQ\), тогда \(PS^2 = AS\cdot BP\).

Аналогично треугольники \(APS\) и \(SCR\) подобны по двум углам, откуда \[\dfrac{PS}{SC} = \dfrac{AP}{SR},\] но \(PS = SR\), тогда \(PS^2 = AP\cdot SC\).

В итоге \[AS\cdot BP = PS^2 = AP\cdot SC,\] что и требовалось доказать.

б) Так как \(PQRS\) квадрат, то \(PS\parallel QR\), откуда следует равенство \(\angle APS = \angle ABC\) как односторонних углов при параллельных прямых и секущей, а также то, что \(AK\perp PS\). Пусть \(M\) – точка пересечения \(AK\) и \(PS\).

Рассмотрим треугольники \(APM\) и \(ABK\): \(\angle APM = \angle ABK\), \(\angle PAM\) – общий, тогда треугольники \(APM\) и \(ABK\) подобны по двум углам, откуда \[\dfrac{AM}{AK} = \dfrac{AP}{AB}.\]

Рассмотрим треугольники \(APS\) и \(ABC\): \(\angle APS = \angle ABC\), \(\angle BAC\) – общий, тогда треугольники \(APS\) и \(ABC\) подобны по двум углам, откуда \[\dfrac{PS}{BC} = \dfrac{AP}{AB}.\]

В итоге \[\dfrac{AM}{AK} = \dfrac{AP}{AB} = \dfrac{PS}{BC},\] следовательно, \[\dfrac{AK - MK}{AK} = \dfrac{PS}{BC}.\] Так как \(PQ\) и \(MK\) – отрезки параллельных прямых, заключённых между параллельными прямыми \(PS\) и \(BC\), то \(MK = PQ\).

\(PS = PQ\), \(AK = 0,5\cdot BC\), тогда \[\dfrac{0,5\cdot BC - PQ}{0,5\cdot BC} = \dfrac{PQ}{BC},\] следовательно, \(BC - 2PQ = PQ\), значит, \[BC = \dfrac{1}{3}\cdot PQ\qquad\Rightarrow\qquad \dfrac{PQ}{BC} = \dfrac{1}{3}.\]

Ответ:

б) \(\dfrac{1}{3}\).

Составим таблицу для первых двух лет (пока Коля учится), обозначив за \(A\) стоимость годового обучения, а за \(t=\dfrac{100+y}{100}\): \[\begin{array}{|l|c|c|} \hline \text{Год} & \text{Сумма долга до начисления }\% & \text{Сумма долга после начисления }\%\\ \hline 1& A & tA \\ \hline 2& tA+A & t(tA+A)=B\\ \hline \end{array}\]

В течение следующих двух лет семья Коли начинает вносить в банк равные ежегодные платежи, чтобы выплатить кредит. Обозначим за \(x\) этот ежегодный платеж: \[\begin{array}{|l|c|c|c|} \hline \text{Год} & \text{Сумма долга до начисления }\% & \text{Сумма долга после начисления }\%& \text{Сумма долга после платежа}\\ \hline 3& B & tB & tB-x \\ \hline 4& tB-x & t(tB-x) & t(tB-x)-x\\ \hline \end{array}\]

Т.к. к концу \(4\)-ого года семья должна выплатить кредит, то \(t(tB-x)-x=0\). Сделав подстановку \(B=t(tA+A)\), получим:

\((t+1)(t^3A-x)=0 \Rightarrow x=t^3 A\). Таким образом, всего банку семья Коли заплатит \(2x\) рублей.

Заметим, что при такой системе в долг у банка семья Коли взяла \(2A\) рублей (сумму за два года обучения), таким образом, переплата составила \(2x-2A\). По условию переплата не должна превышать \(40 \%\) от стоимости кредита, т.е.

\(2x-2A \leqslant 0,4\cdot 2A \Rightarrow x\leqslant 1,4A \Rightarrow t^3 \leqslant 1,4 \Rightarrow t \leqslant \sqrt[3]{1,4}\).
\(\Rightarrow y \leqslant 100\cdot \sqrt[3]{1,4}-100\)

Преобразуем число \(100\cdot \sqrt[3]{1,4}-100\):

\(100\cdot \sqrt[3]{1,4}-100=10\cdot \sqrt[3]{1400}-100=20\cdot \sqrt[3]{175}-100\)

Оценим это число:

\(559<\sqrt[3]{175000000}<560 \Rightarrow 5,59<\sqrt[3]{175}<5,6 \Rightarrow 11,8<20\cdot \sqrt[3]{175}-100<12\)

Таким образом, наибольшая годовая ставка \(y=11 \%\)

Ответ:

\(11\%\).

Перепишем уравнение в виде: \[\sin x \cdot \cos x+2\cos x -2-2\sin x +5x=a\]

и рассмотрим функцию \(f(x)=\sin x \cdot \cos x+2\cos x -2-2\sin x +5x\). Найдем ее производную:

\(\begin{multline*} f'(x)= 5+\cos^2 x-\sin^2 x-2\sin x-2\cos x=5+\cos{2x}-2(\sin x+\cos x)=\\ =5+\cos {2x} -2\sqrt2 \left(\dfrac{\sqrt2}{2}\sin x + \dfrac{\sqrt2}{2}\cos x\right)=5+\cos {2x}-2\sqrt 2 \cdot \sin {\left(x+\dfrac{\pi}{4}\right)} \end{multline*}\)

Т.к. \(-1\leqslant \cos {2x}\leqslant 1, \ \ \ -1\leqslant \sin {\left(x+\dfrac{\pi}{4}\right)}\leqslant 1 \Rightarrow \ \ \ f'(x)\geqslant 4-2\sqrt2>0 \) при всех значениях \(x\).

Следовательно, \(f(x)\) – строго возрастающая функция. Значит, уравнение \(f(x)=a\) может иметь не более одного решения при всех значениях \(a\). Для того, чтобы \(x_o\) являлось решением уравнения, нужно, чтобы \(a=f(x_o)\).

Т.к. функция \(f(x)\) – строго возрастает, то если \(x_o\) пробегает отрезок \(\left[0;\dfrac{\pi}{2}\right]\), то множеством значений функции \(f(x)\) является отрезок \(\left[f(0); f \left( \dfrac{\pi}{2} \right)\right]\).

Таким образом, \(a\in \left[4; \dfrac{5\pi}{2}\right]\).

Ответ:

\(a\in \left[ 4; \dfrac{5\pi}{2} \right]\).

Так как место Тимура за столом фиксировано, то можно считать, что его за столом не будет (ответ от этого не изменится).

Пусть Тимур как-то занумеровал стулья. Тогда на первый стул может претендовать любой из \(6\) гостей.

Какой бы из \(6\) гостей не занял первый стул, на второй стул может претендовать любой из оставшихся на этот момент \(5\) гостей. \[\dots\]

На последний шестой стул будет претендовать один единственный гость.

В итоге: каждый из \(6\) вариантов для первого стула даёт пять различных вариантов для второго стула и т.д., то есть всего есть \(6! = 1\cdot 2\cdot 3\cdot 4\cdot 5\cdot 6 = 720\) различных способов рассадить гостей.

Ответ:

\(720\)