Задачи по стереометрии

Т.к. \(A_1C\parallel \alpha \Rightarrow A_1C\) параллельна некоторой прямой, содержащейся в \(\alpha\). Рассмотрим плоскость \(AA_1C_1C\), в которой находится \(A_1C\). Т.к. точка \(K\in AA_1C_1C\), то проведем в этой плоскости \(KN \parallel A_1C\) (по теореме Фалеса \(N\) – середина \(AC\)).

Т.к. \(ABCDA_1B_1C_1D_1\) – куб, то \(N\) – точка пересечения диагоналей квадрата \(ABCD\), следовательно, \(N\in BD\). Таким образом, получили сечение \(KBD\) куба плоскостью \(\alpha\).

Ответ:

Рисунок.

Т.к. грани \(ADD_1A_1\) и \(BCC_1B_1\) куба параллельны, то плоскость \(DMN\) пересечет их по параллельным прямым. Таким образом, проведем \(NK\parallel DM\). Таким образом, \(DNKM\) – искомое сечение.

Необходимо найти точное расположение точки \(K\).

Обозначим ребро куба за \(6x\). Т.к. \(\bigtriangleup ADM \sim \bigtriangleup BNK \Rightarrow \dfrac{BK}{AM}=\dfrac{BN}{AD} \Rightarrow BK=2x\). Таким образом, \(BK:KB_1=1:2\).

Ответ:

Рисунок.

1) Пусть \(AC\cap BD=O\). Две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.



Заметим, что т.к. \(\angle SAB=\angle SAD=90^\circ \Rightarrow SA\perp (ABC)\).

Проведем в плоскости \(SAC\) прямую \(OK\parallel SC\). Т.к. \(O\) – середина \(AC\), то по теореме Фалеса \(K\) – середина \(SA\). Через точку \(K\) в плоскости \(SAB\) проведем \(KM\parallel SB\) (следовательно, \(M\) – середина \(AB\)). Таким образом, плоскость, проходящая через прямые \(OK\) и \(KM\), и будет искомой плоскостью.

Необходимо найти сечение пирамиды этой плоскостью. Соединив точки \(O\) и \(M\), получим прямую \(MN\).

Т.к. \(\alpha\parallel (SBC)\),то \(\alpha\) пересечет плоскость \(SCD\) по прямой \(NP\parallel SC\) (если \(NP\cap SC \ne \varnothing\), то \(\alpha\cap (SBC)\ne \varnothing\), что невозможно ввиду их параллельности).

Таким образом, \(KMNP\) – искомое сечение, причем \(KP\parallel AD\parallel MN \Rightarrow\) это трапеция.

2) Т.к. все точки \(K,M,N,P\) – середины отрезков \(SA, AB, CD, SD\) соответственно, то:

а) \(MN=AD=a\)

б) \(KP=\dfrac{1}{2}AD=\dfrac{a}{2}\)

в) \(KM=\dfrac{1}{2}SB=\dfrac{a\sqrt2}{2}\)

Заметим, что по теореме о трех перпендикулярах \(SB\perp BC \Rightarrow KM\perp MN\). Таким образом, \(KMNP\) – прямоугольная трапеция.

\(S_{KMNP}=\dfrac{KP+MN}{2}\cdot KM=\dfrac{3\sqrt2}{8}a^2\)

Ответ:

1) Рисунок.

2) \(\dfrac{3\sqrt2}{8}a^2\)

1) Пусть\(K\) – середина \(AC\), \(SX, AL\) – медианы грани \(ASB\), \(CL, SY\) – медианы грани \(CSB\), \(AL\cap SX=M, CL\cap SY=N\). \(SO\) – высота пирамиды.

Найдем сечение пирамиды плоскостью \(MNK\).
Т.к. пирамида правильная, то \(\triangle SXY\) – равнобедренный, \(SM=SN=\dfrac{2}{3}SX \Rightarrow MN\parallel XY \Rightarrow MN\parallel (ABC)\). Таким образом, плоскость \(MNK\) содержит прямую \(MN\), параллельную \(ABC\), следовательно, плоскость \(MNK\) пересечет плоскость \(ABC\) по прямой, параллельной \(MN\) (если это не так, то линия пересечения этих плоскостей \(l\cap MN=E \Rightarrow E\in (ABC)\) и \(E\in MN \Rightarrow MN\) не может быть параллельна \((ABC)\)).

Прямая, проходящая через точку \(K\) и параллельная \(MN\) (или \(XY\)) – это \(AC\). Следовательно, сечением является равнобедренный треугольник \(ALC\).

2) Пусть \(LK\cap SO=H\). Тогда по теореме о трех перпендикулярах \(HK\perp AC\) как наклонная (\(HO\perp (ABC), OK\perp AC\) как проекция). Следовательно, и \(LK\perp AC\).

Тогда \(S_{ALC}=\dfrac{1}{2}AC\cdot LK\).

Рассмотрим \(\triangle SKB: \ BK=AB\cdot \dfrac{\sqrt3}{2}=\dfrac{21\sqrt3}{2} \Rightarrow \cos B=\dfrac{7\sqrt3}{12\sqrt2}\).

Тогда по теореме косинусов для \(\triangle KLB\):

\(KL^2=\dfrac{729}{4} \Rightarrow KL=\dfrac{27}{2}\)

Значит, \(S_{ALC}=\dfrac{567}{4}\).

Ответ:

\(\dfrac{567}{4}\).

1) Если \(A_1O\perp \alpha\), то \(A_1O\) перпендикулярно двум пересекающимся прямым, лежащим в плоскости \(\alpha\). Построим эти две прямые.

Рассмотрим плоскость \(AA_1C_1C\) (\(A_1O\) лежит в этой плоскости). Проведем в ней \(AQ\perp A_1O\). Теперь необходимо через их точку пересечения (точку \(Q\)) провести еще одну прямую перпендикулярно \(A_1O\).

Рассмотрим для этого плоскость \(A_1BD\) (\(A_1O\) лежит в этой плоскости). Проведем через точку \(Q\) прямую \(RS\perp A_1O\). Т.к. по теореме о трех перпендикулярах \(A_1O\perp BD\) как наклонная (\(A_1A\perp (ABC), AO\perp BD\) – проекция), то \(RS\parallel BD\).

2) Проведем прямые \(AR\) и \(AS\). Они могут пересечь либо сами ребра \(DD_1\) и \(BB_1\), либо их продолжения. Т.к. от этого зависит вид сечения, определим расположение точек \(R\) и \(S\).

Обозначим ребро куба за \(a\). Тогда \(AO=\dfrac{a\sqrt2}{2}=\dfrac a{\sqrt2}\). Рассмотрим прямоугольный \(\triangle AA_1O\). Так как \(AQ\perp A_1O\), то по свойству прямоугольного треугольника \(\triangle AA_1Q\sim \triangle AA_1O\). Следовательно, \[\dfrac{A_1Q}{AA_1}=\dfrac{AA_1}{A_1O}\] Так как по теореме Пифагора \(A_1O=\sqrt{a^2+\frac{a^2}2}=\dfrac{\sqrt6 a}2\), то \[A_1Q=\dfrac{AA_1^2}{A_1O}=\dfrac{\sqrt6}3a\]

Так как \(RS\parallel BD\), то \(\triangle A_1DO\sim \triangle A_1RQ\), следовательно, \[\dfrac{A_1R}{A_1D}=\dfrac{A_1Q}{A_1O}=\dfrac{\sqrt6}3:\dfrac{\sqrt6}2= \dfrac23\] Аналогично \(A_1S:A_1B=2:3\).

Заметим, что \(\triangle AA_1R\sim \triangle MDR\) с коэффициентом подобия \(2\) (\(A_1R:RD=2:1\)), следовательно, \(MD=\frac12AA_1\).
Аналогично \(PB=\frac12AA_1\).

Таким образом, получили линии пересечения плоскостей \(AA_1D_1\) и \(AA_1B_1\) с плоскостью \(\alpha\) – прямые \(AM\) и \(AP\).

3) Так как плоскости \(AA_1B_1\) и \(DD_1C_1\) параллельны, то плоскость \(\alpha\) пересечет их по параллельным прямым. Следовательно, в плоскости \(DD_1C_1\) через точку \(M\) нужно провести прямую, параллельную \(AP\).
Так как \(M\) и \(P\) – середины \(DD_1\) и \(BB_1\), то \(MC_1\parallel AP\).



Таким образом, сечение куба плоскостью \(\alpha\) – это четырехугольник \(AMC_1P\) (который, вообще говоря, является ромбом, так как \(AM=AP=MC_1\) и \(MC_1\parallel AP\)).

Ответ:

Рисунок.

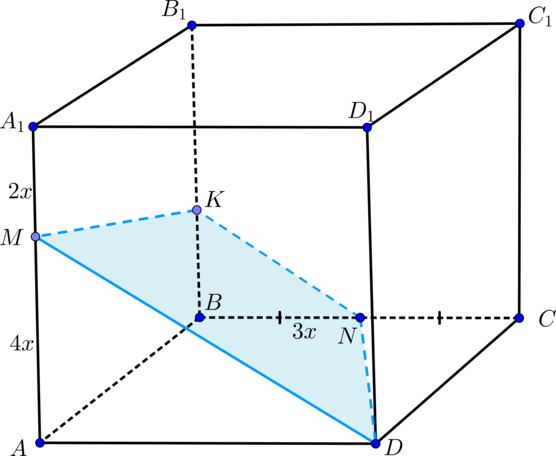
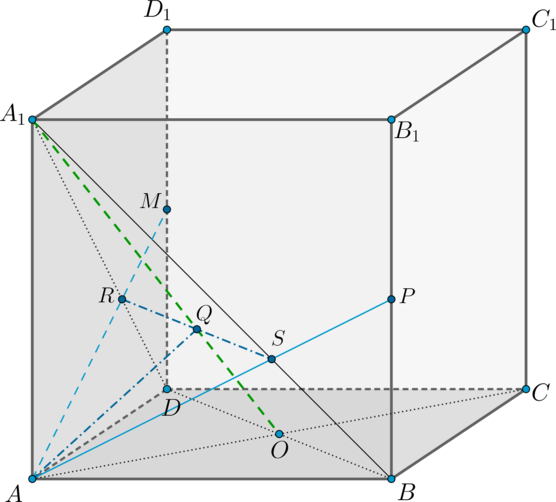
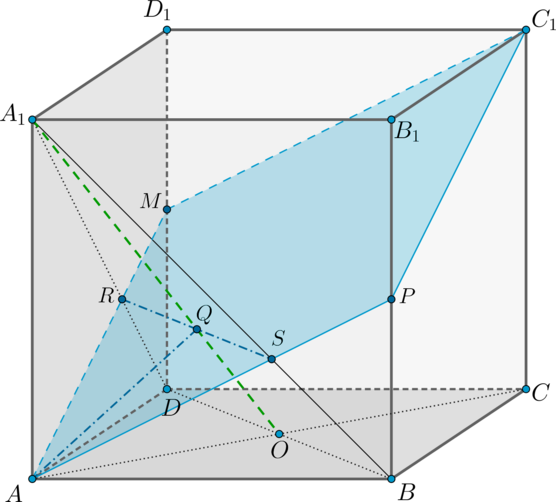
Обозначим ребро основания за \(a\), а боковое ребро за \(b\). Тогда из условия задачи следует, что \(BM=\frac16b\), \(CN=\frac34b\), \(DK=\frac13b\).

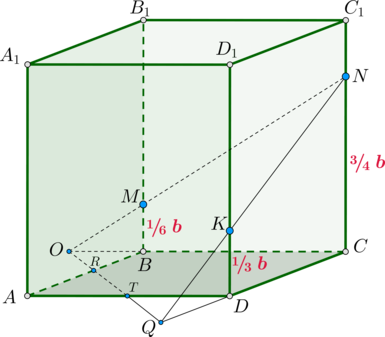
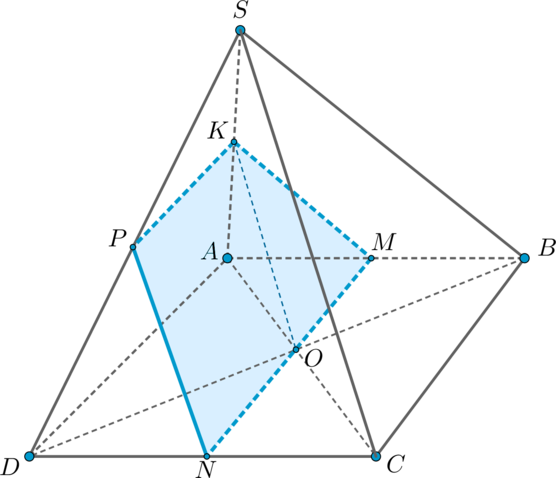
Найдем положение точек \(R\) и \(T\), в которых плоскость пересекает ребра \(AB\) и \(AD\) соответственно.

1) Продлим отрезки \(NK\) и \(CD\) до пересечения в точке \(Q\). Тогда \(\triangle QDK\sim \triangle QNC\). Следовательно,

\[\dfrac{QD}{QC}=\dfrac{KD}{NC} \quad \Rightarrow \quad \dfrac{QD}{QD+a}=\dfrac{\frac13b}{\frac34b}=\dfrac49 \quad \Rightarrow \quad QD=\dfrac45a.\]

Аналогично из \(\triangle OMB\sim \triangle ONC\) получаем, что \[OB=\dfrac27a.\]

Соединив точки \(Q\) и \(O\), получим точки пересечения плоскости с ребрами \(AB\) и \(AD\).

2) Рассмотрим основание.

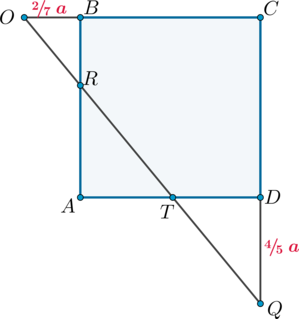
\(\triangle OBR\sim \triangle OCQ\), следовательно,

\[\dfrac{OB}{OC}=\dfrac{BR}{CQ} \quad \Rightarrow \quad \dfrac{\frac27a}{\frac97a}=\dfrac{BR}{\frac95a} \quad \Rightarrow \quad BR=\dfrac25a.\]

\(\triangle OBR\sim \triangle TAR\), следовательно,

\[\dfrac{OB}{AT}=\dfrac{BR}{AR}\quad \Rightarrow \quad \dfrac{\frac27a}{AT}=\dfrac{\frac25a}{\frac35a} \quad \Rightarrow \quad AT=\dfrac37a.\]

3) Для того, чтобы найти, в каком отношении \(RT\) поделит \(AC\), проведем прямую \(RG\parallel AD\), \(G\in AC\).

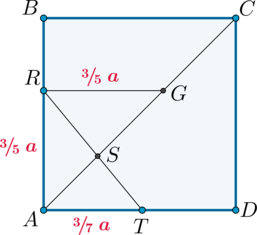
Тогда \(\triangle ARG\) – прямоугольный и \(\angle RAG=45^\circ\), то есть он равнобедренный и \(RG=\frac35a\). Тогда по теореме Фалеса \(AG:AC=AR:AB=3:5\), следовательно, т.к. \(AC=a\sqrt2\), то \(AG=\frac{3\sqrt2}5a\).

\(\triangle AST\sim \triangle RSG\), следовательно,

\[\dfrac{AT}{RG}=\dfrac{AS}{SG} \quad \Rightarrow \quad \dfrac{\frac37a}{\frac35a}=\dfrac{AS}{\frac{3\sqrt2}5a-AS} \quad \Rightarrow \quad AS=\dfrac{\sqrt2}4a.\]

Тогда \(SC=a\sqrt2-\frac{\sqrt2}4a=\frac{3\sqrt2}4a\) и \(AS:SC=1:3\).

Ответ:

\(1:3\)