Найдите наименьшее значение функции \(y = 2x^2\cdot e^{x} - 3\).
1) \[y' = 4x\cdot e^{x} + 2x^2\cdot e^{x} = 2x(x + 2)\cdot e^x\]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна \(0\) или не существует): \[2x(x + 2)\cdot e^x = 0\qquad\Leftrightarrow\qquad x(x + 2) = 0\,,\] откуда находим корни \(x_1 = -2\), \(x_2 = 0\). Производная функции \(y\) существует при любом \(x\). Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её график.
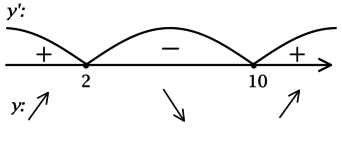
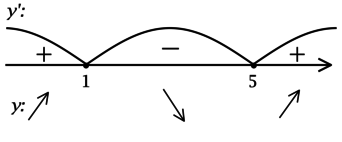
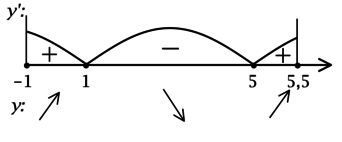
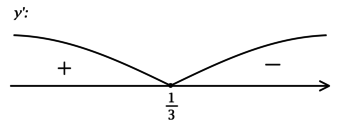
2) Найдём промежутки знакопостоянства \(y'\):
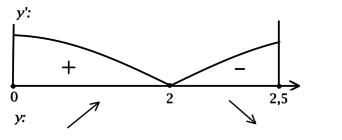
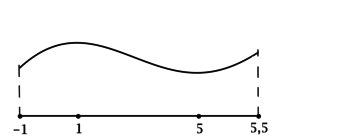
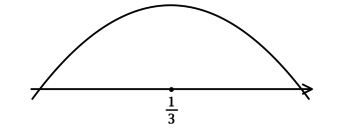
3) Эскиз графика \(y\):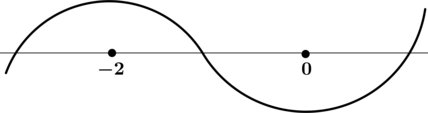
По полученному эскизу нельзя сказать наверняка, действительно ли в точке локального минимума \(x = 0\) значение функции наименьшее, или же при каком-то отрицательном \(x\) значение функции окажется меньше, чем при \(x = 0\). Найдём \(y(0)\): \[y(0) = 2\cdot 0\cdot e^{0} - 3 = -3\,.\] Рассмотрим произвольное \(x_0 < 0\), тогда \[y(x_0) = 2{x_0}^2\cdot e^{x_0} - 3\,,\] но \({x_0}^2\geqslant 0\) и \(e^{x_0}\geqslant 0\), тогда \[y(x_0) = 2{x_0}^2\cdot e^{x_0} - 3\geqslant 0 - 3\geqslant -3\,,\] следовательно, наименьшее значение функции \(y\) равно \(y(0) = -3\).
Ответ: -3