Задачи по планиметрии формата ЕГЭ

а) Пусть \(AO\) пересекает \(BC\) в точке \(A_1\). Тогда по теореме Менелая для \(\triangle BAA_1\) и прямой \(CC_1\): \[\dfrac{BC_1}{C_1A}\cdot \dfrac{AO}{OA_1}\cdot \dfrac{A_1C}{CB}=1\] По теореме Менелая для \(\triangle CAA_1\) и прямой \(BB_1\): \[\dfrac{AB_1}{B_1C}\cdot \dfrac{CB}{BA_1}\cdot \dfrac{A_1O}{OA}=1\] Перемножив два этих равенства, получим: \[\dfrac{A_1C}{A_1B}=1 \quad\Rightarrow\quad A_1C=A_1B\] Чтд.

б) Из первого равенства имеем: \[\dfrac{BC_1}{C_1A}\cdot \dfrac{AO}{OA_1}\cdot \dfrac{A_1C}{CB}=1 \quad\Rightarrow\quad \dfrac21\cdot \dfrac{AO}{OA_1}\cdot \dfrac12=1\] Отсюда \(AO=OA_1\).
Пусть \(S_{OAC_1}=S\), тогда \(S_{OBC_1}=2S\), так как площади треугольников, имеющих одинаковую высоту, относятся как основания. Так как \(AO=OA_1\), то \(3S=S_{OBA}=S_{OBA_1}\). Аналогично \(S_{OCA_1}=S_{OBA_1}=3S\). Аналогично \(S_{OCA}=S_{OCA_1}=3S\). Так как \(S_{OAB_1}:S_{OCB_1}=1:2\), то \(S_{OAB_1}=S, S_{OCB_1}=2S\).



Следовательно, \[\dfrac{S_{AB_1OC_1}}{S_{ABC}}=\dfrac{2S}{12S}=\dfrac16\]

Ответ:

б) \(1:6\)

а) Так как окружность вписана, то ее центр лежит на пересечении биссектрис углов трапеции. Следовательно, \(\angle KAO=\angle NAO\), \(\angle KBO=\angle LBO\). Так как \(\angle A+\angle B=180^\circ\) (по определению трапеции), то \[\angle KAO+\angle KBO=\dfrac12\cdot \left(\angle A+\angle B\right)= 90^\circ \quad\Rightarrow\quad \angle AOB=180^\circ-90^\circ=90^\circ\] Аналогично доказывается, что \(\angle COD=90^\circ\). Тогда из прямоугольных \(\triangle AOB\) и \(\triangle COD\): \[\begin{aligned} &AO^2+BO^2=AB^2\\ &CO^2+DO^2=CD^2\\ &\Rightarrow\quad AO^2+BO^2+CO^2+DO^2=AB^2+CD^2 \end{aligned}\]

б) Так как окружность вписана, то \(AK=AN=9\), \(BK=BL=4\), \(CL=CM=1\), \(DN=DM=x\). Обозначим также радиус окружности за \(r\).
По теореме Пифагора из \(\triangle BKO\): \[BO^2=16+r^2;\] из \(\triangle AKO\): \[AO^2=81+r^2.\] Тогда из \(\triangle AOB\): \[81+r^2+16+r^2=13^2 \quad\Rightarrow\quad r=6.\] Аналогично, \[CO^2=37, \quad DO^2=36+x^2\quad\Rightarrow\quad 37+36+x^2=(x+1)^2 \quad\Rightarrow\quad x=36.\] Тогда площадь трапеции равна произведению полупериметра на радиус вписанной окружности: \[S_{ABCD}=(9+4+1+36)\cdot 6=300.\]

Ответ:

б) 300

а) Перепишем равенство, которое нужно доказать, в следующий вид: \[\dfrac{CF}{AD}=\dfrac{CE}{AB} \quad\Leftrightarrow\quad \dfrac{CF}{ED}=\dfrac{CE}{EB} \quad (*)\] Докажем, что \(ED=FD\). Тогда из теоремы Фалеса, так как \(EF\parallel DB\), будет следовать, что равенство \((*)\) верно.



\(\angle ADB=\angle AFE\) как соответственные при \(EF\parallel DB\) и \(AC\) секущей. \(\angle BDE=\angle FED\) как накрест лежащие при \(EF\parallel DB\) и \(ED\) секущей.
\(\triangle ADB=\triangle EDB\) по трем сторонам, следовательно, \(\angle ADB=\angle BDE\).
Следовательно, \(\angle FED=\angle BDE=\angle ADB=\angle AFE\), откуда \(\triangle DFE\) равнобедренный и \(ED=FD\).

б) Проведем \(AE\).



\(ADEB\) – дельтоид, следовательно, его диагонали взаимно перпендикулярны, то есть \(AE\perp DB\).
(Докажем это. Пусть \(AE\cap DB=O\). Так как \(\triangle ADE\) равнобедренный, то \(DO\) – высота, следовательно, \(DB\perp AE\).)
Следовательно, \(\angle FEO=\angle DOE=90^\circ\) (так как если \(OE\perp DB\), \(DB\parallel FE\), то \(OE\perp FE\)).
Заметим, что \(\angle DEF=90^\circ-30^\circ=60^\circ\), следовательно, \(\triangle DEF\) – равносторонний, то есть \(FE=DF=DE\).
Также заметим, что \(\angle DEO=\angle DAO=\angle DBE=\angle DBA=30^\circ\). А \(\angle OAB=90^\circ-\angle OBA=60^\circ\).
Следовательно, \(\angle BAC=90^\circ\), \(\angle ABC=60^\circ\), следовательно, \(\angle ACB=30^\circ\).
Таким образом, \(\triangle CFE\) равнобедренный (\(\angle FEC=\angle FCE=30^\circ\)), следовательно, \(FC=FE=FD\).
Следовательно, точки \(D\) и \(F\) разбивают \(AC\) на три равных отрезка.
Заметим, что \(\triangle DEC=\triangle DEB\) как прямоугольные по общему катету и острым углам, следовательно, \(EC=EB\).

По теореме Менелая для \(\triangle CBA\) и прямой \(LE\): \[\dfrac{AD}{DC}\cdot \dfrac{CE}{EB}\cdot \dfrac{BL}{LA}=1 \quad\Rightarrow \quad \dfrac{BL}{LA}=\dfrac21\quad\Rightarrow\quad BL=2LA\quad\Rightarrow\quad AB=AL\] Следовательно, \(BL=BC\) и \(\triangle LBC\) равнобедренный, а так как \(\angle LBC=60^\circ\), то равносторонний. Значит, \(AB=\frac12LB=\frac12CL=3\).
Тогда \[\sqrt3=\mathrm{tg}\,60^\circ=\dfrac{AC}{AB} \quad\Rightarrow\quad AC=3\sqrt3\] Тогда \[S_{\triangle ABC}=\dfrac12\cdot AC\cdot AB=\dfrac92\sqrt3\]

Ответ:

б) \(\frac92\sqrt3\)

а)

Пусть \(O\) – центр первой окружности, \(Q\) – центр второй. Докажем, что точки \(A, O, D\) лежат на одной прямой (то есть что \(AD\) – диаметр). Так как \(OA\perp AB\), \(QB\perp AB\) (как радиусы, проведенные в точки касания), то \(AO\parallel BQ\). Следовательно, \(\angle AOL+\angle BQL=180^\circ\) как односторонние углы при \(AO\parallel BQ\) и \(OQ\) секущей.
\(\angle BLQ=\angle OLD\) как вертикальные.
Заметим, что \(\triangle BLQ\) и \(\triangle LOD\) – равнобедренные, причем их углы при основании равны, следовательно, равны и углы при вершине: \(\angle LOD=\angle BQL\). Таким образом, \(\angle AOL+\angle LOD=180^\circ\), следовательно, точки \(A, O, D\) лежат на одной прямой.
Аналогично доказывается, что точки \(B, Q, C\) лежат на одной прямой.
Следовательно, \(AD\perp AB\), \(BC\perp AB\), откуда \(AD\parallel BC\), чтд.

б)

Обозначим \(\angle OLA=\alpha\), \(\angle QLB=\beta\). Тогда \(\angle AOL=180^\circ-2\alpha\), \(\angle BQL=180^\circ-2\beta\).
Тогда \(180^\circ-2\alpha+180^\circ-2\beta=180^\circ\), откуда \(\alpha+\beta=90^\circ\). Следовательно, \(\angle ALB=180^\circ-90^\circ=90^\circ\), то есть \(\triangle ALB\) – прямоугольный с гипотенузой \(AB\).
Проведем \(OH\perp BQ\). Тогда \(ABHO\) – прямоугольник (все углы прямые), следовательно, \(HQ=BQ-AO=8-2=6\). Из прямоугольного \(\triangle OHQ\) по теореме Пифагора: \[OH=\sqrt{OQ^2-HQ^2}=8\] Так как \(ABHO\) прямоугольник, то \(AB=OH=8\).
\(\triangle ABC\) также прямоугольный (\(\angle B=90^\circ\)), следовательно, \[AC=\sqrt{AB^2+BC^2}=8\sqrt5\] Заметим, что \(\triangle AOL\sim \triangle CQL\), следовательно, \[\dfrac{AL}{LC}=\dfrac{AO}{CQ}=\dfrac 28\] Следовательно, \[AL=\dfrac15AC=\dfrac8{\sqrt5}\] Тогда по теореме Пифагора из \(\triangle ALB\): \[BL=\sqrt{AB^2-AL^2}=\dfrac{16}{\sqrt5}\] Следовательно, \[S_{ALB}=\dfrac12\cdot AL\cdot BL=\dfrac{64}5\]

Ответ:

б) \(\frac{64}5\)

а) У параллелограмма противоположные стороны равны: \(AB=CD, BC=AD\). Так как в четырехугольник вписана окружность, то суммы его противоположных сторон равны, следовательно, \[AB+CD=BC+AD \quad\Rightarrow\quad 2AB=2BC \quad\Rightarrow\quad AB=BC=CD=AD\] Следовательно, по определению \(ABCD\) – ромб.

б) Найдем площадь четырехугольника \(A_1B_1C_1D_1\).



Докажем, что \(A_1B_1C_1D_1\) – прямоугольник.
Так как \(OA_1\perp AB, OC_1\perp CD\), то точки \(A_1, O, C_1\) лежат на одной прямой, следовательно, \(A_1C_1\) – высота ромба. Аналогично \(B_1D_1\) – высота, то есть \(A_1C_1=B_1D_1\) (1). Также \(OA_1=OB_1=OC_1=OD_1\) (2). Так как диагонали четырехугольника точкой пересечения делятся пополам – (2), то это параллелограмм. Так как диагонали параллелограмма равны – (1), то это – прямоугольник.
Пусть \(BB_1=BA_1=3, CB_1=CC_1=5\).
Заметим, что \(\angle A_1OB_1=360^\circ-\angle OA_1B-\angle OB_1B-\angle B=180^\circ-\angle B\). Аналогично \(\angle B_1OC_1=180^\circ-\angle C\). Следовательно, \(\angle A_1OB_1=\angle C=\alpha\), \(\angle B_1OC_1=\angle B=\beta\).
Тогда \(\triangle A_1OB_1\sim\triangle B_1CC_1\), \(\triangle B_1OC_1\sim \triangle A_1BB_1\) как равнобедренные по двум углам (например, \(\angle OA_1B_1=0,5(180^\circ-\alpha)=\angle B_1C_1C\), \(\angle A_1OB_1=\angle C\) по доказанному ранее).
Найдем по теореме косинусов \(A_1B_1\) и \(B_1C_1\): \[\begin{aligned} &A_1B_1^2=3^2+3^2-2\cdot 3\cdot 3\cdot \cos\beta=3^2\cdot 2(1-\cos \beta)\\[1ex] &B_1C_1^2=5^2+5^2-2\cdot 5\cdot 5\cdot \cos\alpha=5^2\cdot2 (1-\cos\alpha) \end{aligned}\quad (*)\] Из двух подобий, указанный ранее, следует \[\dfrac{OA_1}{CC_1}=\dfrac{A_1B_1}{B_1C_1} \quad {\small{\text{и}}} \quad \dfrac{BB_1}{OB_1}=\dfrac{A_1B_1}{B_1C_1}\] Разделим первое равенство на второе и получим \[\dfrac{OA_1\cdot OB_1}{CC_1\cdot BB_1}=1 \quad\Rightarrow\quad \dfrac{OA_1^2}{3\cdot 5}=1\quad\Rightarrow\quad OA_1=\sqrt{15}\] Тогда первое равенство можно переписать в виде: \[\dfrac{\sqrt{15}}{5}=\dfrac{A_1B_1}{B_1C_1}\] откуда находим, что \(5A_1B_1^2=3B_1C_1^2\). Подставим в полученное равенство правые части равенств из \((*)\), учитывая, что, так как \(\alpha+\beta=180^\circ\), то \(\cos\beta=-\cos\alpha\): \[5\cdot 3^2\cdot 2(1-\cos\beta)=3\cdot 5^2\cdot 2(1+\cos\beta) \quad\Rightarrow\quad \cos\beta=-\dfrac14 \quad\Rightarrow\quad \cos\alpha=\dfrac14\] Следовательно, \[\begin{aligned} &A_1B_1=3\cdot \sqrt{\dfrac52}\\[2ex] &B_1C_1=5\cdot \sqrt{\dfrac32} \end{aligned}\] Следовательно, площадь \[S_{A_1B_1C_1D_1}=A_1B_1\cdot B_1C_1=7,5\sqrt{15}\]

Ответ:

\(7,5\sqrt{15}\)

а) Так как обе окружности вписаны в угол \(ACB\), то их центры лежат на биссектрисе угла \(ACB\). Рассмотрим чертеж:
Заметим, что \(\dfrac{5\sqrt5}{3\sqrt3}=\dfrac{5\sqrt{15}}9>\dfrac{\sqrt{15}}3\), следовательно, центр второй окружности находится дальше от вершины \(C\), чем центр окружности, вписанной в \(\triangle ABC\).
Так как окружности касаются, то их центры и точка касания лежат на одной прямой. \(OM=OT\) –радиусы, следовательно, \(\triangle OMT\) – равнобедренный. Аналогично \(\triangle QKT\) – равнобедренный. Пусть \(\angle OMT=\alpha, \angle QKT=\beta\).
Так как \(\angle OMK=\angle QKM=90^\circ\) (так как радиус, проведенный в точку касания, перпендикулярен касательной), то \(OM\parallel QK\). Следовательно, \(\angle MOQ+\angle KQO=180^\circ\) как односторонние (: \[180^\circ-2\alpha+180^\circ-2\beta=180^\circ \quad\Leftrightarrow\quad \alpha+\beta=90^\circ\] Отсюда \(\angle KTM=180^\circ-\alpha-\beta=90^\circ\).

б) Проведем \(OH\perp QK\). Следовательно, \(HQ=QK-OM=\frac29\sqrt{15}\). \(OQ=\frac89\sqrt{15}\). Следовательно, \[OH=\sqrt{OQ^2-HQ^2}=\dfrac{10}3\]
Из подобия \(\triangle CKQ\sim\triangle OHQ\): \[\dfrac{CK}{OH}=\dfrac{KQ}{QH}\quad\Rightarrow\quad CK=\dfrac{25}3\] Следовательно, так как \(OH=MK\), то \(CM=\dfrac{25}3-\dfrac{10}3=5\).

Из формулы \(S=pr\) следует, что \(p_{ABC}=9\), откуда \(P_{ABC}=18\).
Так как отрезки касательных, проведенных к окружности из одной точки, равны, то \(CM=CP=5, BP=BR=y, AM=AR=x\). Следовательно, \[AB=\dfrac{P_{ABC}-2CM}2=4=x+y, \quad AC=5+x, \quad BC=5+y\] По формуле Герона: \[S_{ABC}=\sqrt{9\cdot (9-4)(9-5-x)(9-5-y)}=3\sqrt{15}\quad\Rightarrow\quad (4-x)(4-y)=3\] Так как \(x+y=4\), то получаем уравнение \[y^2-4y+3=0\quad\Rightarrow\quad y=1; \quad y=3\] Если \(y=1\), то \(x=3\); если \(y=3\), то \(x=1\).
Так как \(AC\) – большая сторона, то \(AC>BC\), откуда \(x>y\). Следовательно, подходят \(x=3, y=1\).
Следовательно, \(AB=4, AC=8, BC=6\).
По теореме косинусов \[\cos\angle ABC=\dfrac{AB^2+BC^2-AC^2}{2AB\cdot BC}=-\dfrac14\] Следовательно, \(\sin\angle ABC=\dfrac{\sqrt{15}}4\). Тогда \[\mathrm{tg}\,\angle ABC=-\sqrt{15}\]

Ответ:

\(-\sqrt{15}\)

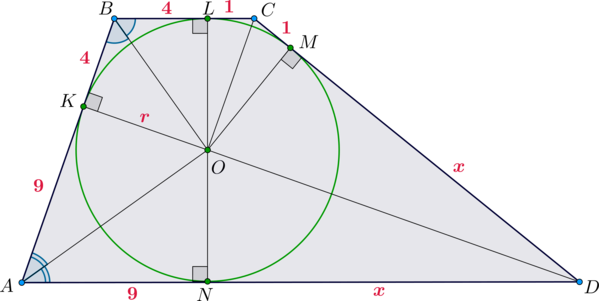
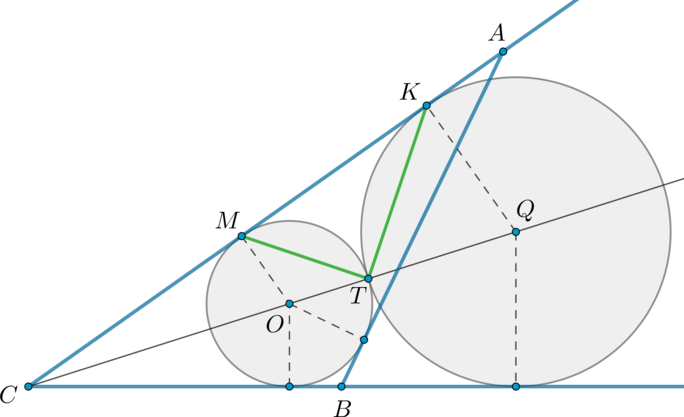
а) Пусть \(R_1, R_2, R_3\) – точки касания со стороной \(AC\) окружностей с центрами \(O_1, O_2, O_3\) соответственно.
Тогда \(O_1R_1, O_2R_2, O_3R_3\perp AC\).

Если окружность вписана в угол, то она лежит на биссектрисе этого угла, следовательно, \(O_1, O_3\) лежат на биссектрисе угла \(C\), \(O_1, O_2\) – на биссектрисе угла \(A\).
Будем называть окружность с центром в \(O_1\) – первой, с центром в \(O_2\) – второй и с центром в \(O_3\) – третьей.

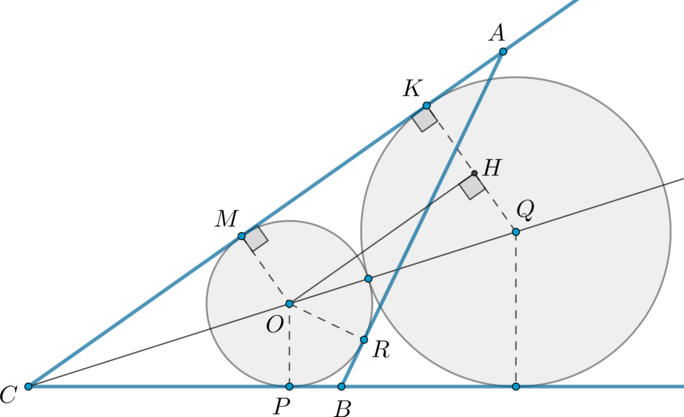
Пусть \(KK_3\) – общая касательная к первой и третьей окружностям. \(LL_2\) – общая касательная к первой и второй окружностям, как показано на рисунке: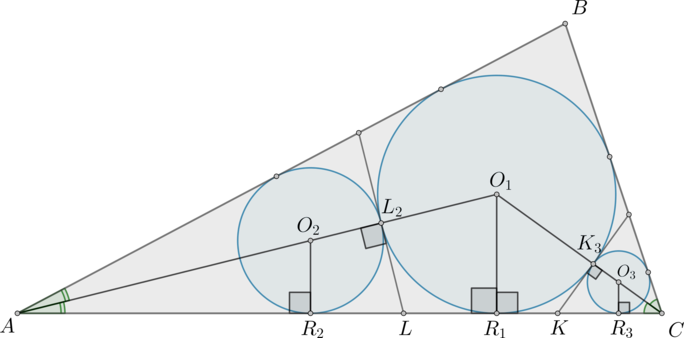
Докажем, что \(\angle CK_3K=\angle AL_2L=90^\circ\).
Так как \(KK_3\) – касательная, \(K_3\) – точка касания, то \(\angle KK_3O_3=90^\circ\) как угол между касательной и радиусом, проведенным в точку касания. Аналогично \(\angle AL_2L=90^\circ\).

Заметим также, что \(KR_3=KK_3=KR_1\) и \(LR_2=LL_2=LR_1\) (также как отрезки касательных).

Рассмотрим “правую” часть рисунка.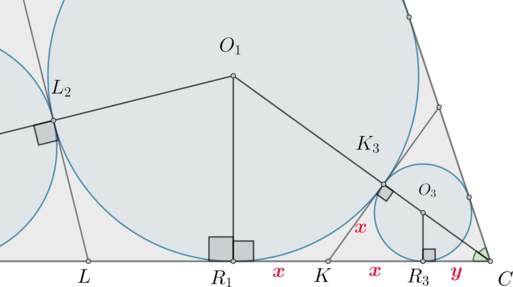
Заметим, что \(\triangle CO_3R_3\sim \triangle CKK_3\sim \triangle CO_1R_1\) (по двум углам). Обозначим \(CR_3=y, KR_3=x\). Тогда из подобия этих трех треугольников \[\dfrac{O_3R_3}{CR_3}=\dfrac{KK_3}{K_3C}=\dfrac{O_1R_1}{CR_1} \quad\Rightarrow\quad \dfrac 1y=\dfrac{x}{\sqrt{(x+y)^2-x^2}}=\dfrac9{2x+y}\] Из равенства \[\dfrac 1y=\dfrac9{2x+y}\] можно выразить \(x\) через \(y\): \(x=4y\). Тогда \(K_3C=\sqrt{(x+y)^2-x^2}=3y\), следовательно, \[\mathrm{tg}\,\dfrac{\angle C}2=\dfrac x{3y}=\dfrac43\] Тогда \(\angle C=2\mathrm{arctg}\,\frac43\).
Докажем, что это значение действительно равно \(180^\circ-\mathrm{arctg}\,\frac{24}7\).
Найдем тангенс \(\angle C\), полученного в нашем решении, и тангенс \(\angle C\), данного в условии: \[\begin{aligned} &\mathrm{tg}\,\left(2\mathrm{arctg}\,\dfrac43\right)= \dfrac{2\mathrm{tg}\,\left(\mathrm{arctg}\,\dfrac43\right)}{1- \mathrm{tg}\,^2\left(\mathrm{arctg}\,\dfrac43\right)}= \dfrac{2\cdot \frac43}{1-\left(\frac43\right)^2}=-\dfrac{24}7\\[2ex] &\mathrm{tg}\,\left(180^\circ-\mathrm{arctg}\,\frac{24}7\right)=- \mathrm{tg}\,\left(\mathrm{arctg}\,\frac{24}7\right)=-\dfrac{24}7 \end{aligned}\] Чтд.

б) Для того, чтобы найти площадь \(\triangle AO_1O_3\), можно найти площадь \(\triangle AO_1C\) и вычесть из нее площадь \(\triangle AO_3C\). Высоты этих треугольников к основанию \(AC\) мы знаем, следовательно, нужно найти \(AC\).
Найдем \(y\).
Рассмотрим уже выведенное равенство из пункта а): \[\dfrac 1y=\dfrac{x}{\sqrt{(x+y)^2-x^2}}\quad\rightarrow\quad \dfrac 1y=\dfrac {4y}{3y}\quad\Rightarrow\quad y=\dfrac34\] Следовательно, \(R_1C=9y=\frac{27}4\).
Теперь нужно найти \(AR_1\).
Для этого воспользуемся тем же способом, что и в пункте а). Пусть \(AR_2=t\), \(R_2L=z\). Так как \(\triangle AO_2R_2\sim \triangle ALL_2\sim \triangle AO_1R_1\), то \[\dfrac{81}{25t}=\dfrac{z}{\sqrt{(z+t)^2-z^2}}=\dfrac9{2z+t}\] Отсюда \(z=\frac89t\). Так же, как в пункте а), найдем, что \(t=\frac{243}{40}\). Следовательно, \(AR_1=t+2z=\frac{25}9t=\frac{135}8\). Тогда \[S_{AO_1O_3}=S_{AO_1C}-S_{AO_3C}=\dfrac 12\cdot AC\cdot (O_1R_1-O_3R_3)= \dfrac12\cdot \left(\dfrac{135}8+\dfrac{27}4\right)\cdot 8=94,5\]

Ответ:

б) 94,5