Если выпускник готовится к сдаче ЕГЭ по математике и при этом рассчитывает на получение конкурентных баллов, ему непременно стоит освоить принцип решения задач на клетчатой бумаге. Подобные планиметрические задания каждый год включаются в программу аттестационного испытания. Таким образом, справляться с задачами ЕГЭ на клетчатой бумаге должны все учащиеся, независимо от уровня их подготовки.
Полезная информация
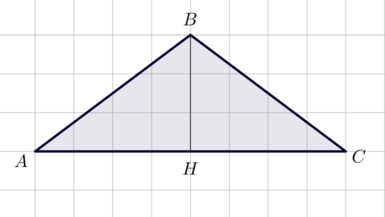
Задания ЕГЭ на клетчатой бумаге часто решаются гораздо проще, чем задачи, для выполнения которых требуется применение аналитических методов. Чаще всего в подобных упражнениях необходимо найти площадь фигуры. Решить такие задачи можно, вспомнив основные теоремы и свойства трапеции, треугольника, шестиугольника и т. д.
Как подготовиться к экзамену?
Если задания ЕГЭ на клетчатой бумаге вызывают у вас трудности, обратитесь к образовательному порталу «Школково». С нами вы сможете повторить материал по темам, которые являются для вас сложными, например, векторы на координатной плоскости и таким образом восполнить пробелы в знаниях. В разделе «Теоретическая справка» представлена вся базовая информация. Ее наши специалисты подготовили и изложили в максимально доступной форме на основе богатого практического опыта.
Освоить принцип решения задач на клетчатой бумаге помогут упражнения, представленные в разделе «Каталог». Мы подготовили простые и более сложные задания. Тренироваться в их выполнении учащиеся из Москвы и других российских городов могут в онлайн-режиме.
Справившись с заданием, выпускники имеют возможность сохранить его в разделе «Избранное». Это позволит в дальнейшем вернуться к нему и, к примеру, обсудить алгоритм его решения со школьным преподавателем. База заданий на сайте «Школково» регулярно обновляется.