Теме «Построение сечения» в ЕГЭ по математике профильного уровня посвящается, как правило, несколько заданий. Они могут требовать от школьника как краткого ответа, так и полного развернутого решения. Если одним из ваших слабых мест являются именно задачи на сечения (в ЕГЭ при этом вы хотите получить конкурентные баллы), непременно стоит повторить или вновь разобраться в материале.
Сделать это наиболее эффективно вам поможет образовательный математический проект «Школково». Наши специалисты подготовили теоретический материал, изложив его таким образом, чтобы школьники с любым уровнем подготовки смогли восполнить пробелы в знаниях и легко справиться с решением задач на сечение.
Полезная информация
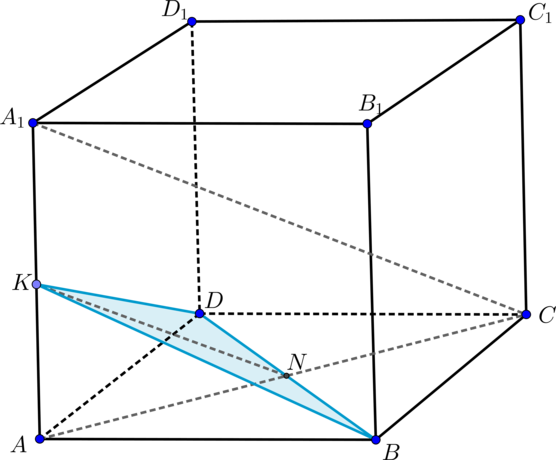
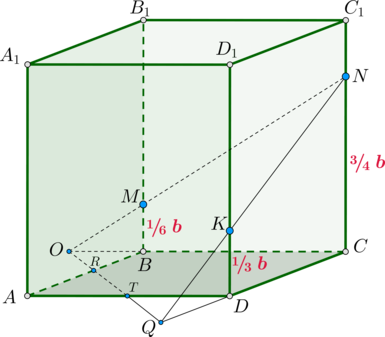
Для того чтобы выполнить построение сечений в ЕГЭ, нужно отметить точки пересечения пространственной фигуры с ребрами и произвести их соединение, начертив отрезки.
Необходимо запомнить
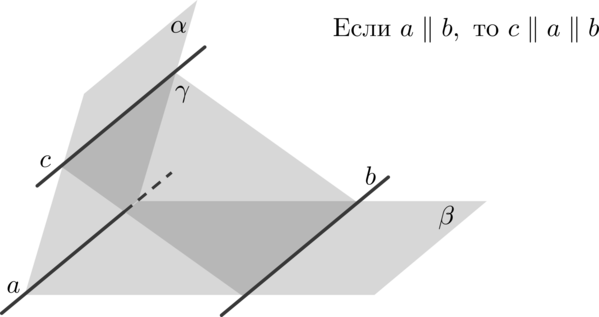
Производится соединение только двух точек, которые лежат в плоскости одной грани. Прежде чем приступить к решению задачи на построение сечений, полезно повторить материал о параллельных прямых. Сделать это вы можете, посетив раздел «Теоретическая справка».
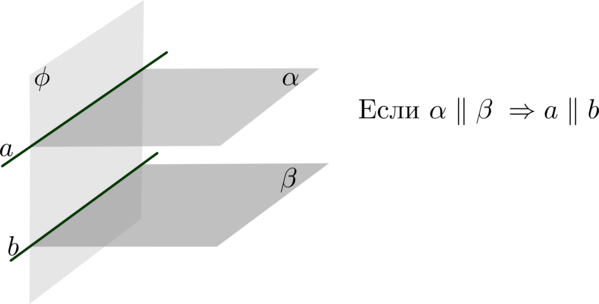
Также необходимо запомнить, что пересечение секущей плоскости параллельных граней возможно только по параллельным отрезкам.
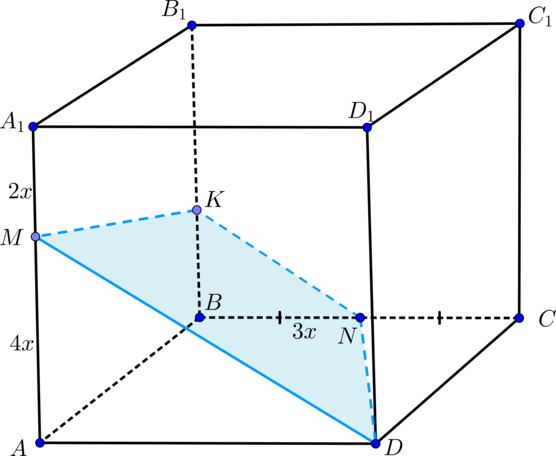
В том случае, когда в плоскости грани обозначена только одна точка, которая принадлежит плоскости сечения, следует отметить еще одну дополнительную. Для того чтобы это сделать, нужно определить точки пересечения прямых, которые уже построены, с теми, которые лежат в тех же гранях.
Выполнив построение сечений многогранников в задачах, которые представлены в нашем «Каталоге», вы сможете закрепить изученный материал и успешно справиться с подобным заданием на ЕГЭ в Москве.