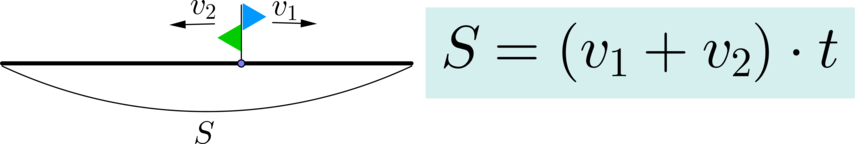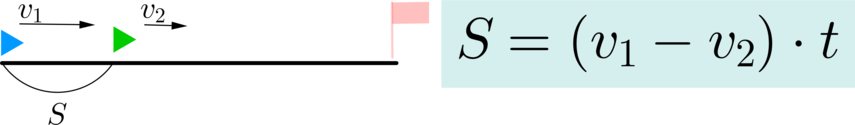Задачи на прямолинейное движение в ЕГЭ по математике могут быть как совсем простыми, без необходимости вводить переменную, так и более сложными, где требуется свести задание к решению квадратного уравнения. Для успешного выполнения подобного упражнения школьнику необходимо прежде всего запомнить следующую формулу:
\[{\large{S=V\cdot t}}\] где \(S\) — пройденное расстояние, \(V\) — скорость, \(t\) — время, в течение которого двигалось тело.
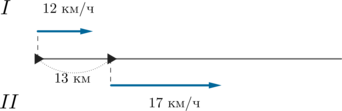
Для того чтобы решить задачи на прямолинейное движение в ЕГЭ, учащимся из Москвы и других городов также для большей наглядности стоит выполнить чертеж. На нем нужно отметить все векторы, о которых идет речь в условии упражнения.
Для того чтобы правильно решить задачи на прямолинейное движение в ЕГЭ и получить заветные баллы, многим школьникам необходимо восполнить пробелы в знаниях по данной теме. Поможет в этом образовательный проект «Школково». Наш ресурс предоставляет возможность не только повторить теоретический материал, но и познакомиться с различными вариантами решения заданий по данной теме.