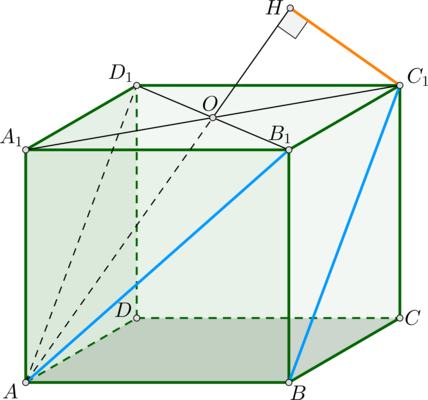
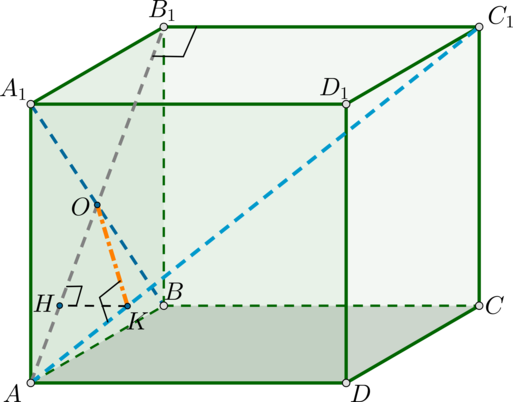
В кубе \(ABCDA_1B_1C_1D_1\), ребро которого равно \(\sqrt{32}\), найдите расстояние между прямыми \(DB_1\) и \(CC_1\).
Прямые \(DB_1\) и \(CC_1\) скрещиваются по признаку, т.к. прямая \(DB_1\) пересекает плоскость \((DD_1C_1)\), в которой лежит \(CC_1\), в точке \(D\), не лежащей на \(CC_1\).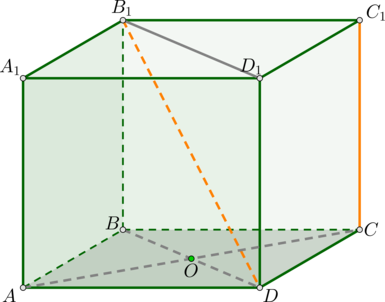
Расстояние между скрещивающимися прямыми будем искать как расстояние между прямой \(CC_1\) и плоскостью, проходящей через \(DB_1\) параллельно \(CC_1\). Т.к. \(DD_1\parallel CC_1\), то плоскость \((B_1D_1D)\) параллельна \(CC_1\).
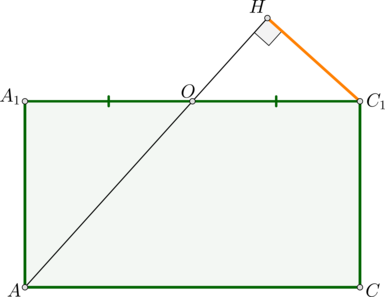
Докажем, что \(CO\) – перпендикуляр на эту плоскость. Действительно, \(CO\perp BD\) (как диагонали квадрата) и \(CO\perp DD_1\) (т.к. ребро \(DD_1\) перпендикулярно всей плоскости \((ABC)\)). Таким образом, \(CO\) перпендикулярен двум пересекающимся прямым из плоскости, следовательно, \(CO\perp (B_1D_1D)\).
\(AC\), как диагональ квадрата, равна \(AB\sqrt2\), то есть \(AC=\sqrt{32}\cdot \sqrt2=8\). Тогда \(CO=\frac12\cdot AC=4\).
Ответ: 4