Многолетняя практика подтверждает тот факт, что задачи ЕГЭ на комбинированные поверхности вызывают у выпускников определенные затруднения. При этом подобные задания из раздела «Геометрия в пространстве» включаются в программу аттестационного испытания по математике из года в год. В связи с этим вспомнить базовые алгоритмы выполнения подобных задач просто необходимо.
Как подготовиться к экзамену?
Хотите решать геометрические задачи по теме «Комбинированные поверхности», не допуская ошибок? Для этого достаточно усвоить несложный алгоритм нахождения правильного ответа.
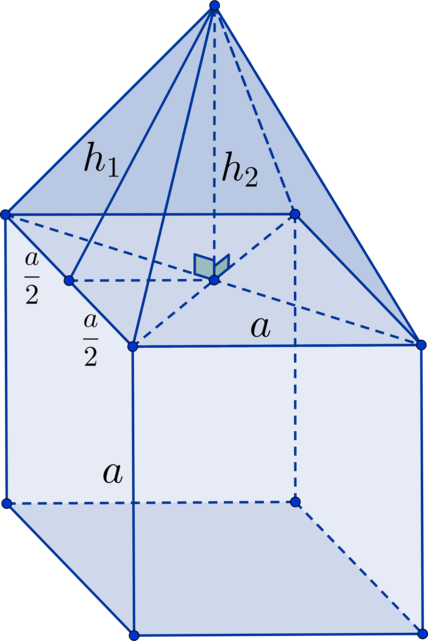
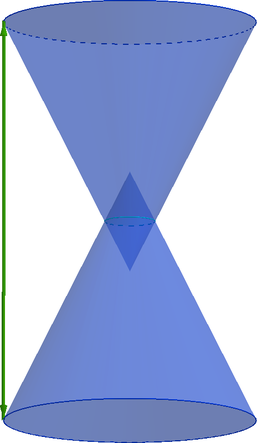
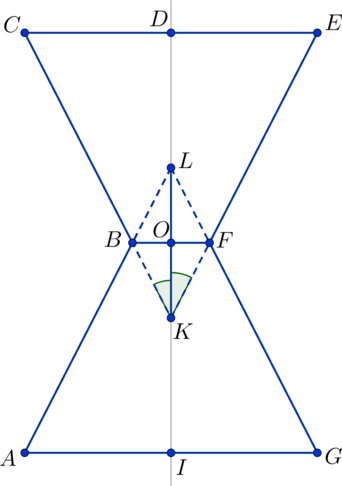
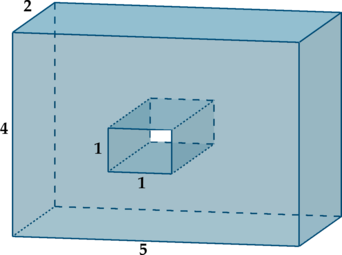
- Для вычисления объема, площади или других неизвестных параметров комбинированной фигуры необходимо прежде всего поделить ее на известные элементы.
- Затем рекомендуем вспомнить основные формулы получившихся фигур.
- Освежив в памяти эту информацию и правильно применив ее, вы сможете рассчитать искомый параметр.
Чтобы подготовка к сдаче единого государственного экзамена была действительно качественной и эффективной, занимайтесь вместе с математическим порталом «Школково». Для того чтобы задачи ЕГЭ по теме «Комбинированные фигуры» не вызывали у старшеклассников особых затруднений, вначале им непременно стоит освежить в памяти базовый теоретический материал. Причем для этого вовсе не обязательно искать нужный параграф в школьном учебнике. Весь необходимый материал уже собран и понятно изложен в разделе «Теоретическая справка».
Чтобы применить полученные знания на практике, предлагаем выпускникам попрактиковаться в выполнении онлайн-задач, например, на тему «Вписанные и описанные поверхности». Чтобы найти соответствующие упражнения, достаточно перейти в раздел «Каталог». База заданий регулярно дополняется. Для каждого упражнения на сайте мы прописали алгоритм решения и правильный ответ.
Чтобы в случае необходимости быстро найти задание, вы можете сохранить его в разделе «Избранное». Это позволит вам в любой момент вернуться к нему и обсудить принцип его выполнения со школьным учителем или репетитором.