После каникул рост Маши стал 5 футов 3 дюйма. Выразите её рост в метрах, если 1 фут принять равным 30 см, а 1 дюйм принять равным 2,5 см.
Рост Маши стал \(5 \cdot 30 + 3 \cdot 2,5 = 157,5\) сантиметров, что составляет 1,575 метра.
Ответ: 1,575
Тренировочные варианты "Школково". Уровень составитель ЕГЭ
После каникул рост Маши стал 5 футов 3 дюйма. Выразите её рост в метрах, если 1 фут принять равным 30 см, а 1 дюйм принять равным 2,5 см.
Рост Маши стал \(5 \cdot 30 + 3 \cdot 2,5 = 157,5\) сантиметров, что составляет 1,575 метра.
Ответ: 1,575
На диаграмме показана среднедневная температура воздуха в Нижнем Новгороде за первые 14 дней апреля. По вертикали указывается температура в градусах Цельсия, по горизонтали – дни месяца. Определите по диаграмме, сколько за указанный период было дней, когда среднедневная температура превышала 4,5 градуса Цельсия.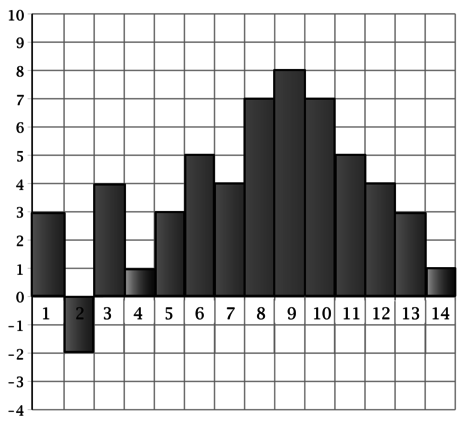
По диаграмме видно, что среднедневная температура превышала 4,5 градуса Цельсия 6, 8, 9, 10 и 11 апреля. Итого: 5 дней.
Ответ: 5
В треугольнике \(ABC\) точка \(H\) делит сторону \(AB\) в отношении \(\dfrac{2}3\), считая от вершины \(B\). Найдите площадь треугольника \(HBC\), если площадь \(S_{ABC} = 15\).
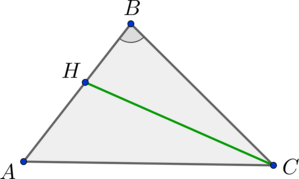
Треугольники \(ABC\) и \(HBC\) имеют общий угол \(B\), следовательно:
\(\dfrac{S_{BHC}}{S_{ABC}} = \dfrac{HB\cdot BC}{AB\cdot BC} = \dfrac{HB}{AB}\).
Пусть \(HB = 2x\), \(AH = 3x\), учитывая то, что \(AB = HB + AH\) получаем:
\(\dfrac{HB}{AH} = \dfrac{2x}{2x+3x} = \dfrac{2}5 \Rightarrow S_{HBC} = S_{ABC}\cdot \dfrac{2}5 = 6\).
Ответ: 6
Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,05. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система контроля забракует неисправную батарейку, равна 0,96. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,04. Найдите вероятность того, что выбранная изготовленная батарейка будет забракована системой контроля.
Выберем произвольную батарейку. Нам удовлетворяют два случая: либо батарейка исправна, но система по ошибке ее забраковала (событие A), либо батарейка неисправна и система ее забраковала (событие B).
Так как это событие имеет вид: “событие A ИЛИ событие B” (причем события несовместны, то есть не могут произойти одновременно!), то вероятность его наступления равна сумме вероятностей событий A и B: \[P=P(A)+P(B)\] Найдем отдельно \(P(A)\) и \(P(B)\).
1) событие A = батарейка исправна И система по ошибке ее забраковала.
Следовательно, вероятность события A равна произведению вероятностей событий “батарейка исправна” и “система забраковала”. Так как вероятность того, что батарейка неисправна, равна 0,05, то вероятность того, что она исправна, равна \(1-0,05=0,95\). Следовательно, \[P(A)=0,95\cdot 0,04=0,038.\]
2) событие B = батарейка неисправна И система ее забраковала.
Следовательно, аналогично событию A, вероятность события B равна произведению вероятностей событий “батарейка неисправна” и “система забраковала”. Следовательно, \[P(B)=0,05\cdot 0,96=0,048.\]
Таким образом, \[P=0,048+0,038=0,086.\]
Ответ: 0,086
Найдите корень уравнения \(\log_{100}(2015x + 1) = \log_{100}(2016x + 1)\).
ОДЗ: \(2015x + 1 > 0\) и \(2016x + 1 > 0\), что равносильно \(x > -\dfrac{1}{2016}\). Решим на ОДЗ: Данное уравнение имеет стандартный вид, оно равносильно \(2015x + 1 = 2016x + 1\), что равносильно \(x = 0\) – подходит по ОДЗ.
Ответ: 0
Около треугольника \(ABC\) описана окружность с центром в точке \(O\). \(\angle BAO=15^\circ, \angle CBO=40^\circ\). Найдите \( \angle ACO\). Ответ дайте в градусах.
Рассмотрим картинку: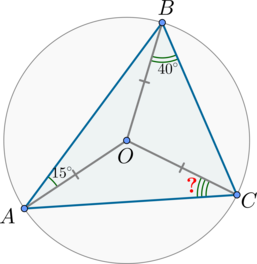
Т.к. треугольники \(AOB\), \(BOC\), \(COA\) – равнобедренные, то \(\angle OBA=15^\circ, \angle OCB=40^\circ\), \(\angle OCA=\angle OAC=\alpha\).
Т.к. сумма углов треугольника \(ABC\) равна \(180^\circ\), то \[(15^\circ+\alpha)+(\alpha+40^\circ)+(40^\circ+15^\circ)=180^\circ \quad
\Rightarrow \quad 2\alpha=180^\circ-2(15^\circ+40^\circ)=70^\circ
\quad \Rightarrow \quad \alpha=35^\circ.\]
Ответ: 35
\(F(x) = x^3 - 2x + 7\) – одна из первообразных функции \(f(x)\). Найдите \(f(0)\).
По определению первообразной \(f(x) = F'(x)\).
Тогда \(f(x) = 3x^2 - 2\), откуда \(f(0) = -2\).
Ответ: -2
Дана четырехугольная пирамида, все ребра которой равны, причем основание является квадратом. Найдите \(6\cos \alpha\), где \(\alpha\) – угол между ее смежными боковыми гранями.
Пусть \(SABCD\) – данная пирамида (\(S\) – вершина), ребра которой равны \(a\). Следовательно, все боковые грани представляют собой равные равносторонние треугольники. Найдем угол между гранями \(SAD\) и \(SCD\).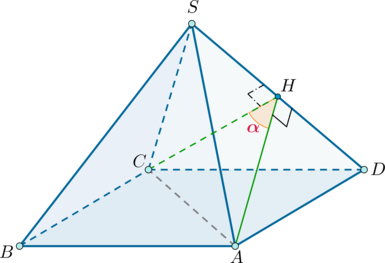
Проведем \(CH\perp SD\). Так как \(\triangle SAD=\triangle SCD\), то \(AH\) также будет высотой в \(\triangle SAD\). Следовательно, по определению \(\angle AHC=\alpha\) – линейный угол двугранного угла между гранями \(SAD\) и \(SCD\).
Так как в основании лежит квадрат, то \(AC=a\sqrt2\). Заметим также, что \(CH=AH\) – высота равностороннего треугольника со стороной \(a\), следовательно, \(CH=AH=\frac{\sqrt3}2a\).
Тогда по теореме косинусов из \(\triangle AHC\): \[\cos \alpha=\dfrac{CH^2+AH^2-AC^2}{2CH\cdot AH}=-\dfrac13 \quad\Rightarrow\quad
6\cos\alpha=-2.\]
Ответ: -2
Найдите значение выражения
\[\sqrt{25^{\frac1{\log_65}}+49^{\frac1{\log_87}}}\]
Применим формулу \(\frac1{\log_ba}=\log_ab\) для показателей, тогда выражение преобразуется к виду
\[\sqrt{25^{\log_56}+49^{\log_78}}=\sqrt{\left(5^2\right)^{\log_56}+\left(7^2\right)^{\log_78}}= \sqrt{5^{2\cdot\log_56}+7^{2\cdot\log_78}}=\sqrt{5^{\log_5{6^2}}+7^{\log_7{8^2}}}\]
Применим формулу \(a^{\log_ab}=b\):
\[\sqrt{6^2+8^2}=\sqrt{100}=10\]
Ответ: 10
Эсминец “Тихий” плывет с постоянной скоростью \(v_0 = 33\) узла (1 узел = 1 морская миля в час). В момент времени \(t = 0\) часов он выпускает торпеду, которая до попадания в цель разгоняется с постоянным ускорением \(a = 66\) узлов в час. Расстояние в морских милях от места пуска торпеды до торпеды определяется из формулы \[S = v_0t+\dfrac{at^2}{2}.\] Определите время с момента пуска (в часах), за которое торпеда поразит неподвижную цель, если расстояние от цели до места пуска торпеды равно \(0,6732\) морских миль.
Время, за которое торпеда поразит неподвижную цель, можно найти из уравнения \[v_0t+\dfrac{at^2}{2} = 0,6732,\] что при учёте значений для скорости и ускорения равносильно \[33t + 33t^2 = 0,6732 \quad\Leftrightarrow\quad t^2+t-0,0204=0\] Дискриминант уравнения \[D=1+0,0816=1,0816=2^6\cdot 13^2\cdot 10^{-4}\quad\Rightarrow\quad \sqrt{D}=2^3\cdot 13\cdot 10^{-2}=1,04.\]
У данного квадратного уравнения имеется два корня \(t_1 = 0,02,\ t_2 = -1,02\), но время \(t > 0\), тогда \(t = 0,02\) часа.
Ответ: 0,02
Два мотоциклиста стартуют одновременно из одной точки круговой трассы в разных направлениях. Скорость первого мотоциклиста в два раза больше, чем скорость второго. Через час после старта они встретились в третий раз (считайте, что в первый раз они встретились уже после старта). Найдите скорость первого мотоциклиста, если длина трассы 40 км. Ответ дайте в км/ч.
В тот момент, когда мотоциклисты встретились в третий раз, суммарное расстояние, которое они проехали, было \(3 \cdot 40 = 120\) км.
Так как скорость первого в 2 раза больше, чем скорость второго, то он проехал из 120 км часть в 2 раза большую, чем второй, то есть 80 км.
Так как встретились в третий раз они через час, то 80 км первый проехал за час. Его скорость 80 км/ч.
Ответ: 80
Найдите наибольшее значение функции \(y = \dfrac{x^2 + x + 1}{x^2 + 1}\) на отрезке \([-10; 1]\).
ОДЗ: \(x\) – произвольный.
1) \[y' = \dfrac{(2x + 1)(x^2 + 1) - 2x\cdot (x^2 + x + 1)}{(x^2 + 1)^2} = \dfrac{-x^2 + 1}{(x^2 + 1)^2}\]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна \(0\) или не существует): \[\dfrac{-x^2 + 1}{(x^2 + 1)^2} = 0\qquad\Leftrightarrow\qquad -\dfrac{(x - 1)(x + 1)}{(x^2 + 1)^2} = 0\,.\] Таким образом, \(y' = 0\) при \(x = -1\) и при \(x = 1\). Производная существует при любом \(x\).
2) Найдём промежутки знакопостоянства \(y'\):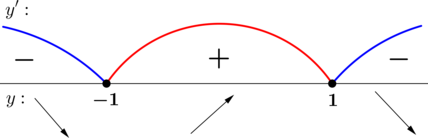
3) Найдём промежутки знакопостоянства \(y'\) на рассматриваемом отрезке \([-10; 1]\):
4) Эскиз графика на отрезке \([-10; 1]\):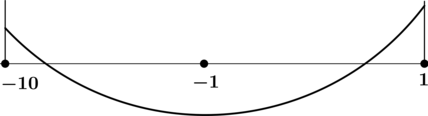
Таким образом, наибольшего на \([-10; 1]\) значения функция достигает в \(x = -10\) или в \(x = 1\). Сравним значения функции в этих точках.
\[y(-10) = \dfrac{100 - 10 + 1}{100 + 1} = \dfrac{91}{101}\qquad y(1) = \dfrac{1 + 1 + 1}{1 + 1} = 1,5\,.\] Итого: \(1,5\) – наибольшее значение функции \(y\) на \([-10; 1]\).
Ответ: 1,5
а) Решите уравнение \[\cos^2x-\dfrac{\sqrt2}2\cos x=\sin \left(\dfrac{\pi}2-x\right)-\dfrac1{\sqrt2}\]
б) Найдите все корни этого уравнения, принадлежащие промежутку \(\left(-\dfrac{\pi}2;\dfrac{\pi}2\right).\)
а) По формуле приведения \(\sin\left(\dfrac{\pi}2-x\right)=\cos x\). Сделаем замену \(t=\cos x\): \[t^2-\dfrac{\sqrt2}2t=t-\dfrac1{\sqrt2} \quad\Leftrightarrow\quad t^2-\left(\dfrac{\sqrt2}2+1\right)t+\dfrac1{\sqrt2}=0\]
Дискриминант уравнения \[D=\left(\dfrac{\sqrt2}2+1\right)^2-\dfrac4{\sqrt2}= \left(\dfrac{\sqrt2}2\right)^2-\sqrt2+1^2=\left(\dfrac{\sqrt2}2-1\right)^2.\]
Следовательно, корнями будут \[t=\dfrac{\frac{\sqrt2}2+1\pm \left(\frac{\sqrt2}2-1\right)}{2} \quad\Rightarrow\quad t_1=\dfrac{\sqrt2}2\quad {\small{\text{и}}}\quad t_2=1.\]
Сделаем обратную замену: \[\begin{aligned} &\cos x=\dfrac{\sqrt2}2\quad\Leftrightarrow\quad x=\pm\dfrac{\pi}4+2\pi m, m\in\mathbb{Z}\\[2ex] &\cos x=1\quad\Leftrightarrow\quad x=2\pi n, n\in\mathbb{Z} \end{aligned}\]
б) Отберем корни.
\(-\dfrac{\pi}2<\dfrac{\pi}4+2\pi m<\dfrac{\pi}2\quad\Leftrightarrow\quad -\dfrac38<m<\dfrac18 \quad\Rightarrow\quad m=0 \quad \Rightarrow\quad x=\dfrac{\pi}4.\)
\(-\dfrac{\pi}2<-\dfrac{\pi}4+2\pi m<\dfrac{\pi}2\quad\Leftrightarrow\quad -\dfrac18<m<\dfrac38 \quad\Rightarrow\quad m=0 \quad\Rightarrow\quad x=-\dfrac{\pi}4.\)
\(-\dfrac{\pi}2<2\pi n<\dfrac{\pi}2\quad\Leftrightarrow\quad -\dfrac14<n<\dfrac14\quad\Rightarrow\quad n=0\quad\Rightarrow\quad x=0.\)
Ответ:
а) \(2\pi n; \quad \pm \dfrac{\pi}4+2\pi m; \quad n,m\in\mathbb{Z}\)
б) \(-\dfrac{\pi}4; \ 0; \ \dfrac{\pi}4\)
В кубе \(ABCDA_1B_1C_1D_1\) все ребра равны \(5\). На его ребре \(BB_1\) отмечена точка \(K\) так, что \(KB=3\). Через точки \(K\) и \(C_1\) проведена плоскость \(\alpha\), параллельная прямой \(BD_1\).
а) Докажите, что \(A_1P:PB_1=1:2\), где \(P\) – точка пересечения плоскости \(\alpha\) с ребром \(A_1B_1\).
б) Найдите объем большей из двух частей куба, на которые он делится плоскостью \(\alpha\).
а) Прямая параллельна плоскости, если плоскость содержит прямую, параллельную данной. Поэтому проведем в плоскости \(BB_1D_1\), содержащей \(BD_1\), прямую \(KN\parallel BD_1\). Пусть \(N\) – точка пересечения с отрезком \(B_1D_1\).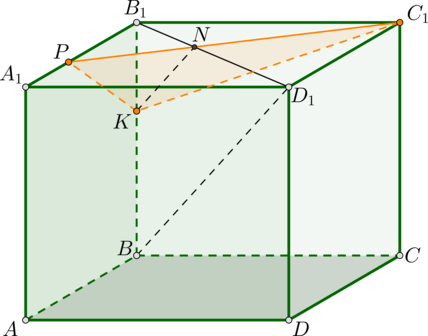
Соединив точки \(C_1\) и \(N\), получим прямую, пересекающую \(A_1B_1\) в точке \(P\).
Т.к. \(KN\parallel BD_1\), то по теореме Фалеса
\[\dfrac{B_1N}{ND_1}=\dfrac{B_1K}{KB}=\dfrac23.\]
Теперь рассмотрим грань \(A_1B_1C_1D_1\). \(\triangle NB_1P\sim \triangle ND_1C_1\), следовательно,
\[\dfrac{PB_1}{C_1D_1}=\dfrac{B_1N}{ND_1}=\dfrac23 \quad \Rightarrow \quad PB_1=\dfrac23C_1D_1=\dfrac23A_1B_1.\]
Следовательно, \(A_1P=\frac13A_1B_1\) и \(A_1P:PB_1=1:2\).
б) Для того, чтобы найти объем большей из частей, на которые плоскость поделила куб, найдем объем куба и вычтем из него объем пирамиды \(PB_1KC_1\).
Заметим, что если рассматривать эту пирамиду как пирамиду с вершиной \(P\) и основанием \(B_1KC_1\), то она является прямоугольной (\(PB_1\perp (B_1KC_1)\)). То есть \(PB_1\) – ее высота, \(\triangle
B_1KC_1\) – основание, являющееся прямоугольным треугольником.
\[V_{PB_1KC_1}=\dfrac13\cdot PB_1\cdot \dfrac12KB_1\cdot B_1C_1= \dfrac13\cdot \dfrac23\cdot 5\cdot \dfrac12\cdot 2\cdot 5=\dfrac{50}9.\]
Объем куба \[V_{ABCDA_1B_1C_1D_1}=5^3=125.\]
Тогда объем большей части равен
\[V=125-\dfrac{50}9=\dfrac{1075}9.\]
Ответ:
б) \(\dfrac{1075}9\)
Решите неравенство \[2^{x+1}\cdot 5^{3-4x}<\dfrac1{10^{4x}}\]
ОДЗ: \(x\) – произвольный.
Т.к. \(\dfrac1{10^{4x}}=10^{-4x}=(2\cdot 5)^{-4x}=2^{-4x}\cdot 5^{-4x}\), то неравенство равносильно: \[2^x\cdot 2\cdot 5^3\cdot 5^{-4x}<2^{-4x}\cdot 5^{-4x} \quad \Leftrightarrow \quad 5^{-4x}\cdot \left(250\cdot 2^x-2^{-4x}\right)<0\] Т.к. по определению \(5^{-4x}>\) при всех \(x\) из ОДЗ, то неравенство равносильно \[250\cdot 2^x-2^{-4x}<0\] Умножим обе части неравенства на положительное выражение \(2^{4x}\) и получим \[250\cdot 2^x\cdot 2^{4x}-2^{-4x}\cdot 2^{4x}<0 \quad \Leftrightarrow \quad 250\cdot 2^{5x}<1 \quad \Leftrightarrow \quad 2^{5x}<250^{-1} \quad \Leftrightarrow \quad 2^{5x}<2^{\log_2{250^{-1}}}\]Т.к. основание больше единицы (\(2>1\)), то неравенство равносильно \[5x<\log_2{250^{-1}} \quad \Leftrightarrow \quad x<-\dfrac{1+3\log_25}5\]
Таким образом, ответ \(x\in \left(-\infty;-\frac{1+3\log_25}5\right)\).
Ответ:
\(\left(-\infty;-\frac{1+3\log_25}5\right)\)
Дан параллелограмм \(ABCD\). Из вершины острого угла \(A\) проведены две прямые, делящие угол на три равные части, причем одна пересекает сторону \(BC\) в точке \(N\), а другая – сторону \(CD\) в точке \(L\), причем \(CN=CL=2\). Известно также, что \(AB=5\). Найдите \(AN+AL\).
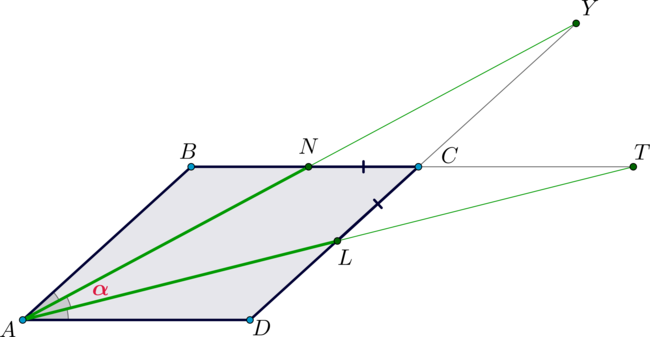
Пусть \(Y\) – точка пересечения прямых \(AN\) и \(CD\), а \(T\) – прямых \(AL\) и \(BC\). Пусть \(\frac13\angle A=\alpha\).
\(\angle CTL=\angle DAL=\alpha\) как накрест лежащие при \(AD\parallel
BC\) и секущей \(AT\). Также \(\angle CYN=\angle BAN=\alpha\) как накрест лежащие при \(AB\parallel CD\) и секущей \(AY\). Заметим, что \(\angle
NCY=\angle LCT\) как вертикальные. Следовательно, в \(\triangle NCY\) и \(\triangle LCT\) равны два угла, следовательно, равны и третьи углы. Также у них \(NC=LC\), следовательно, по признаку “сторона и два прилежащих угла” эти треугольники равны. Значит, \(CY=CT\) и \(NY=LT\).
Тогда \(\triangle ANT=\triangle ALY\), так как \(NT=LY\) и прилежащие углы равны (\(\angle NTA=\angle LYA=\alpha\) по доказанному, \(\angle ANT=\angle ALY=180^\circ-2\alpha\)). Отсюда \(AL=AN=NT=LY\).
Тогда \(\triangle ABN=\triangle ADL\) по этому же признаку (\(\angle
BAN=\angle DAL=\alpha\), \(\angle ABN=\angle ADL\) как противоположные углы параллелограмма \(\Rightarrow\) \(\angle ANB=\angle ALD\)). Значит, \(AD=AB=5\). Следовательно, \(ABCD\) – ромб. Отсюда \(BN=5-2=3\).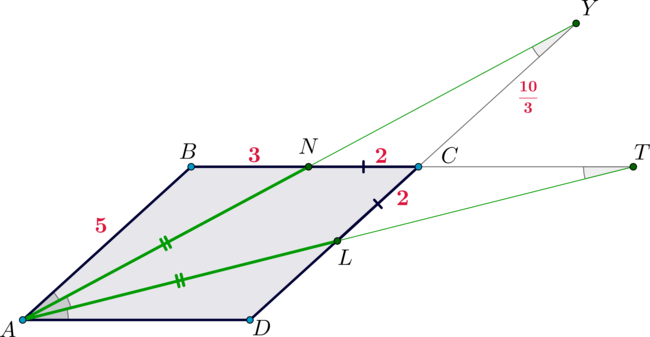
Заметим, что \(\triangle ABN\sim \triangle YCN\) по двум углам, следовательно, \[\dfrac{AB}{CY}=\dfrac{BN}{CN} \quad\Rightarrow\quad
\dfrac5{CY}=\dfrac32 \quad\Rightarrow\quad CY=\dfrac{10}3.\] Тогда по доказанному выше \(AN=AL=LY=2+\frac{10}3=\frac{16}3.\) Тогда \[AN+AL=\dfrac{32}3.\]
Ответ:
\(\dfrac{32}3\)
1 марта Евгений оплатил покупку со своей кредитной карты на \(1\,000\,000\) рублей. Условия пользования кредитной картой таковы:
— долг по карте необходимо погасить в течение 5 месяцев;
— 9 и 27 числа каждого месяца на текущий долг начисляется \(0,1\%\);
— между 9 и 27 числами каждого месяца Евгений имеет возможность внести на карту любую сумму, причем эта сумма идет сначала на погашение начисленных процентов, а оставшаяся часть - на погашение части основного долга. Таким образом, основной долг уменьшается;
— если внесенная таким образом сумма не превышает сумму начисленных процентов, то основной долг не меняется, и происходит лишь погашение части суммы начисленных процентов;
— с 28 числа и до конца месяца Евгений должен внести обязательный платеж по карте так, чтобы сумма долга каждый месяц уменьшалась на одну и ту же величину.
Сколько рублей составит переплата Евгения за совершенную покупку, если помимо обязательных платежей 15 числа каждого месяца Евгений будет вносить на карту \(1000\) рублей?
Т.к. сумма долга каждый месяц должна уменьшаться на одну и ту же величину, а долг необходимо погасить за 5 месяцев, то это значит, что долг разбили на 5 равных частей и каждый месяц он уменьшается на одну такую часть. То есть если долг был равен \(A\) рублей, то в конце первого месяца он будет равен \(A-\frac15A=A-0,2A=0,8A\), в конце второго: \(0,8A-0,2A=0,6A\), в конце третьего: \(0,6A-0,2A=0,4A\) и т.д.
Составим таблицу. Для удобства введем обозначения: \(A=1000\) тыс. рублей, \(1,001=t\):
\[\small{\begin{array}{|c|c|c|c|c|} \hline \text{Долг на 1 число}&\text{Долг на 9 число}& \text{Долг на 15 число}&\text{Долг на 27 число}&\text{Обязательный платеж}\\ \hline A & tA & tA-1 & t(tA-1) & a_1\\ \hline 0,8A & t\cdot 0,8A & t\cdot 0,8A-1 & t(t\cdot 0,8A-1) & a_2\\ \hline 0,6A & t\cdot 0,6A & t\cdot 0,6A-1 & t(t\cdot 0,6A-1) & a_3\\ \hline 0,4A & t\cdot 0,4A & t\cdot 0,4A-1 & t(t\cdot 0,4A-1) & a_4\\ \hline 0,2A & t\cdot 0,2A & t\cdot 0,2A-1 & t(t\cdot 0,2A-1) & a_5\\ \hline \end{array}}\]
Вычислим \(a_i\) платежи. Т.к. до первого обязательного платежа долг был равен \(t(tA-1)\), а после платежа должен стать равным \(0,8A\), то платеж \(a_1=t(tA-1)-0,8A=t^2A-t-A+0,2A=(t^2-1)A-t+0,2A\) (расписали \(0,8A=A-0,2A\)).
Аналогично второй платеж \(a_2=t^2\cdot 0,8A-t-0,6A=t^2\cdot
0,8A-t-0,8A+0,2A=(t^2-1)\cdot 0,8A-t+0,2A\);
третий платеж \(a_3=(t^2-1)\cdot 0,6A-t+0,2A\);
четвертый платеж \(a_4=(t^2-1)\cdot 0,4A-t+0,2A\);
пятый платеж \(a_5=(t^2-1)\cdot 0,2A-t+0,2A\).
Общая сумма выплат по данной карте равна сумме платежей в \(1\) тыс.рублей (их было 5) плюс сумма обязательных платежей:
\(5\cdot 1+a_1+a_2+a_3+a_4+a_5=5+(t^2-1)\cdot A\cdot(1+0,8+0,6+0,4+0,2)-5t+5\cdot 0,2 A=\)
\(=5+(t^2-1)\cdot 3A-5t+A\)
Тогда переплата по кредитной карте равна общей сумме выплат за вычетом суммы, взятой в кредит, то есть за вычетом \(A\):
\[\left(5+(t^2-1)\cdot 3A-5t+A\right)-A=3A\cdot (t^2-1)-5(t-1) \quad \Rightarrow\]
Делая подстановку \(A=1000\), \(t=1,001\), получим:
\[\Rightarrow \quad 3\cdot 1000\cdot 2,001\cdot 0,001-5\cdot 0,001= 5,998\text{ тыс.рублей}=5998 \text{ рублей}\]
Ответ:
\(5998\)
Найдите все значения параметра \(a\), при каждом из которых график функции \[f(x)=3\mathrm{tg}\,\dfrac{ax}5 +2\sin \dfrac{8\pi a-3x}4\]
симметричен относительно начала координат.
Если график функции симметричен относительно начала координат, то такая функция является четной, то есть выполнено \(f(-x)=-f(x)\) для любого \(x\) из области определения функции. Таким образом, требуется найти те значения параметра, при которых выполнено \(f(-x)=-f(x).\)
\[\begin{aligned} &3\mathrm{tg}\,\left(-\dfrac{ax}5\right)+2\sin \dfrac{8\pi a+3x}4= -\left(3\mathrm{tg}\,\left(\dfrac{ax}5\right)+2\sin \dfrac{8\pi a-3x}4\right)\quad \Rightarrow\quad -3\mathrm{tg}\,\dfrac{ax}5+2\sin \dfrac{8\pi a+3x}4= -\left(3\mathrm{tg}\,\left(\dfrac{ax}5\right)+2\sin \dfrac{8\pi a-3x}4\right) \quad \Rightarrow\\[3ex] \Rightarrow\quad &\sin \dfrac{8\pi a+3x}4+\sin \dfrac{8\pi a-3x}4=0 \quad \Rightarrow \quad2\sin \dfrac12\left(\dfrac{8\pi a+3x}4+\dfrac{8\pi a-3x}4\right)\cdot \cos \dfrac12 \left(\dfrac{8\pi a+3x}4-\dfrac{8\pi a-3x}4\right)=0 \quad \Rightarrow\quad \sin (2\pi a)\cdot \cos \frac34 x=0 \end{aligned}\]
Последнее уравнение должно быть выполнено для всех \(x\) из области определения \(f(x)\), следовательно, \(\sin(2\pi a)=0 \Rightarrow a=\dfrac n2, n\in\mathbb{Z}\).
Ответ:
\(\dfrac n2, n\in\mathbb{Z}\)
У Игоря есть гири с массами \(4\) г, \(5\) г, \(6\) г, \(7\) г ..., \(2017\) г.
а) Может ли Игорь уравновесить чашечные весы, использовав все гири разом?
б) Сможет ли Игорь уравновесить чашечные весы, использовав все гири, которые у него будут, когда Тимур подарит ему гирю с массой \(1\) г?
а) Сумма масс имеющихся у Игоря гирь: \(1 + 2 + ... + 2017 - 1 - 2 - 3 = \dfrac{2017\cdot (2017 + 1)}{2} - 6 = 2017\cdot 1009 - 6\) – нечётна, следовательно, имеющиеся у Игоря гири нельзя поставить на весы так, чтобы чаши уравновесились.
б) Так как теперь гирь \(2017 - 3 + 1 = 2015\), то их нельзя разбить на пары. Тогда возьмём и отложим в сторону гири с массами \(1\) г, \(4\) г и \(5\) г.
Разберёмся сначала с остальными гирями – их уже можно разбить на пары так, чтобы суммарные массы во всех парах были одинаковы: \((2017; 6)\), \((2016; 7)\), ..., \((1012; 1011)\) – всего \((2015 - 3) : 2 = 1006\) пар. Теперь можно на одну чашу весов положить все гири, которые попали в первые \(1006 : 2 = 503\) пары, а на другую чашу весов все остальные гири, кроме гирь с массами \(1\) г, \(4\) г и \(5\) г.
На данный момент весы находятся в равновесии, а не использовали мы только те самые гири с массами \(1\) г, \(4\) г и \(5\) г. Остаётся только гирю с массой \(5\) г положить на одну чашу весов (любую), а гири с массами \(1\) г и \(4\) г – на другую чашу весов.
Ответ:
а) Нет
б) Да