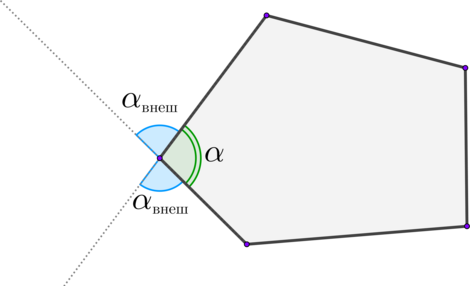
Задания, в которых школьникам необходимо найти внешние углы многоугольника, в ЕГЭ по математике традиционно встречаются из года в год. Правильно решать подобные задачи должны уметь выпускники, сдающие как базовый, так и профильный уровень аттестационного испытания. Школьники, которые освоили задания из раздела «Работа с внешними углами многоугольника», смогут справиться с ЕГЭ и рассчитывать на получение достойных баллов по итогам его прохождения.
Как подготовиться к экзамену?
Перед решением задач на нахождение внешних углов многоугольника в ЕГЭ стоит освежить в памяти определения синуса, косинуса, тангенса и котангенса в прямоугольном треугольнике. Кроме того, для некоторых заданий могут потребоваться формулы основных тригонометрических тождеств.
Восполнить пробелы в знаниях, например, по теме «Вычисление синуса угла треугольника» и лучше усвоить информацию вам поможет образовательный проект «Школково». Для того чтобы выпускники могли успешно справляться с задачами на нахождение внешних углов треугольника в ЕГЭ, мы предоставляем возможность повторить определения и основные правила. Весь необходимый базовый материал вы найдете в разделе «Теоретическая справка». Наши специалисты подобрали соответствующую информацию.
Для закрепления теоретического материала мы предлагаем выполнить упражнения по теме «Работа с внешними углами многоугольника». Подборка простых и сложных заданий представлена в блоке «Каталог». Наши специалисты регулярно обновляют и дополняют упражнения.
Попрактиковаться в решении задач на нахождение внешних углов многоугольника, подобных тем, которые встречаются в ЕГЭ, можно в режиме онлайн, находясь в Москве или любом другом городе России.