Нестандартные графики. Уравнение отрезка

Рассмотрим второе уравнение системы: оно задает семейство прямых \(y=0,2|6-a^2|\), параллельных оси \(Ox\) и лежащих в верхней полуплоскости (включая ось \(Ox\)) при любом значении параметра \(a\) (т.к. модуль всегда неотрицателен).

Рассмотрим первое уравнение. Пусть \(A(x;y)\), \(B(-2;0)\), \(C(0;a)\) – точки. Тогда \(BA=\sqrt{(x+2)^2+y^2}\), \(AC=\sqrt{x^2+(y-a)^2}\), \(BC=\sqrt{4+a^2}\).
Таким образом, первое уравнение системы выглядит так: \(BA+AC=BC\). Значит, оно задает геометрическое место точек \(A\), лежащих на отрезке \(BC\).

Для того, чтобы данная система имела единственное решение, прямая \(y=0,2|6-a^2|\) должна пересекать отрезок \(BC\) в одной точке.

1) Пусть \(a<0\), то есть точка \(C\) лежит на отрицательной части оси \(Oy\). Единственный случай, когда прямая \(y=0,2|6-a^2|\) будет иметь с отрезком одну общую точку, – когда прямая \(y=0,2|6-a^2|\) будет проходить через точку \(B\), то есть совпадать с осью абсцисс. Отсюда \(0,2|6-a^2|=0\), следовательно, \(a=\pm \sqrt6\). Так как \(a<0\), то \(a=-\sqrt6\).

2) Пусть \(a=0\). Тогда отрезок \(BC\) лежит на оси абсцисс, прямая \(y=0,2|6-a^2|\) – в верхней полуплоскости, и общих точек у них нет.

3) Пусть \(a>0\). Тогда \(C\) лежит на положительном направлении оси ординат.

Прямая \(y=0,2|6-a^2|\) пересекает ось ординат в точке \(D\). Для того, чтобы прямая пересекала отрезок \(BC\), нужно, чтобы точка \(C\) находилась не ниже точки \(D\), то есть \[a\geqslant 0,2|6-a^2|\]

Решим данное неравенство. Т.к. \(a>0\), то имеем: \[|6-a^2|\leqslant 5a\quad\Leftrightarrow\quad -5a\leqslant 6-a^2\leqslant 5a\quad\Leftrightarrow\quad 1\leqslant a\leqslant 6.\]

Ответ:

\(a\in\{-\sqrt6\}\cup[1;6]\)

Преобразуем первое уравнение системы. Заметим, что \(a^2+a-2=(a+2)(a-1)\). Заметим также, что \(a+2+a-1=2a+1\), следовательно, по теореме Виета корнями этого уравнения будут \(y=a+2\) и \(y=a-1\). Значит, графиком первого уравнения будут две прямые \(y=a+2\) и \(y=a-1\), параллельные оси абсцисс.

Преобразуем второе уравнение. Рассмотрим точки \(A(a;0)\), \(B(a;3)\), \(C(x;y)\). Тогда \(AB=\sqrt{(a-a)^2+(0-3)^2}=3\), \(AC=\sqrt{(x-a)^2+y^2}\) и \(CB=\sqrt{(x-a)^2+(y-3)^2}\). Следовательно, второе уравнение системы можно переписать в виде \(AC+CB=AB\). Значит, оно задает множество точек \(C\), которые лежат на отрезке \(AB\). Заметим, что так как у точек \(A\) и \(B\) абсцисса одинаковая, то отрезок \(AB\) перпендикулярен оси абсцисс.

Схематично графики обоих уравнений выглядят так:
Чтобы система имела единственное решение, нужно, чтобы зеленый график пересекал отрезок \(AB\) в одной точке. Следовательно, либо прямая \(y=a+2\) пересекает отрезок, а прямая \(y=a-1\) его не пересекает, либо наоборот: \[\left[\begin{gathered}\begin{aligned} &\begin{cases} 0\leqslant a+2\leqslant 3\\ a-1<0 \end{cases} \\ &\begin{cases} 0\leqslant a-1\leqslant 3\\ a+2>3\end{cases} \end{aligned}\end{gathered}\right.\quad\Leftrightarrow\quad a\in [-2;1)\cup(1;4]\]

Ответ:

\([-2;1)\cup(1;4]\)

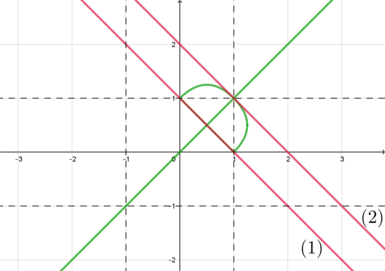
1 способ.

Рассмотрим \(f(x)=\sqrt{(x+8)^2+(x+2)^2}+\sqrt{(x+14)^2+(x+3)^2}\).
Тогда уравнение примет вид \(f(x)=13a\). Тогда нам нужно найти наименьшее значение \(a\), при котором прямая \(y=13a\) будет пересекать график \(y=f(x)\) хотя бы в одной точке. Исследуем \(f(x)\). Для этого найдем сначала ее производную: \[\begin{aligned} &f'(x)=\dfrac{2(x+8)+2(x+2)}{2\sqrt{(x+8)^2+(x+2)^2}}+ \dfrac{2(x+14)+2(x+3)}{2\sqrt{(x+14)^2+(x+3)^2}}=\\[2ex] &=\dfrac{2x+10}{\sqrt{(x+8)^2+(x+2)^2}}+ \dfrac{2x+17}{\sqrt{(x+14)^2+(x+3)^2}} \end{aligned}\] Найдем нули производной: \[\begin{aligned} &\dfrac{2x+10}{\sqrt{(x+8)^2+(x+2)^2}}+ \dfrac{2x+17}{\sqrt{(x+14)^2+(x+3)^2}}=0 \quad\Leftrightarrow\\[2ex] &\sqrt{\dfrac{(x+14)^2+(x+3)^2}{(x+8)^2+(x+2)^2}}=-\dfrac{2x+17}{2x+10} \quad\Leftrightarrow\\[2ex] &\begin{cases} \dfrac{(x+14)^2+(x+3)^2}{(x+8)^2+(x+2)^2}=\left(\dfrac{2x+17}{2x+10}\right)^2 \qquad (*)\\[2ex] \dfrac{2x+17}{2x+10}\leqslant 0\end{cases} \quad\Leftrightarrow\\[2ex] &\begin{cases} 85x^2+598x+424=0\\ x\in \left[-8,5; -5\right) \end{cases} \quad\Leftrightarrow\\[2ex] & x=-\dfrac{106}{17} \end{aligned}\]

Определим знаки производной:


Следовательно, схематично график функции выглядит так:


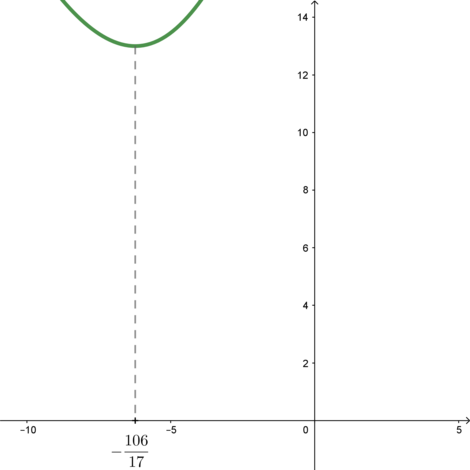
Следовательно, наименьшее значение параметра \(a\) – когда прямая \(y=13a\) проходит через точку экстремума функции \(f(x)\): \[13a=f\left(-\dfrac{106}{17}\right)\quad\Leftrightarrow\quad 13a=13\quad\Leftrightarrow\quad a=1\]

2 способ.

Заметим, что в первом способе было очень много вычислений и на самом деле нам повезло, что при решении уравнения \((*)\) слагаемые с \(x^4\) и \(x^3\) взаимно уничтожились и мы пришли к квадратному уравнению. А что делать, если числа так хорошо не подобраны и мы не получим в конечном итоге “красивое” уравнение, которое сможем решить?
Давайте рассмотрим второй способ решения подобных уравнений.

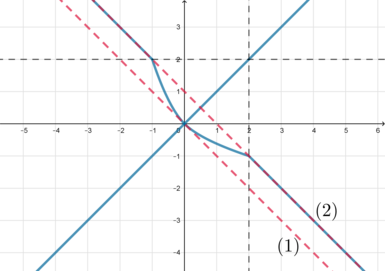
Рассмотрим три точки: \(A(x;x)\), \(B(-8; -2)\), \(C(-14; -3)\). Тогда уравнение примет вид \[AB+AC=13a\] Если нам нужно найти наименьшее значение параметра \(a\), при котором уравнение имеет хотя бы одно решение, то нам нужно найти точку \(A\), при которой сумма длин отрезков \(AB\) и \(AC\) будет наименьшей.
Где располагается точка \(A\)? Эта точка “бегает” по прямой \(y=x\). Графически это выглядит так:


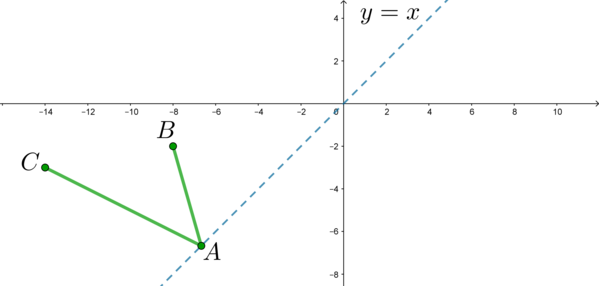
Здесь мы будем использовать классическую идею планиметрии. Отразим симметрично точку \(B\) относительно прямой \(y=x\) (то есть проведем \(BB'\perp y=x\), где \(BH=HB'\):


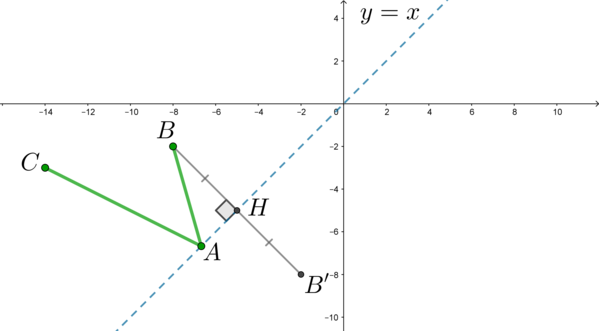
Тогда \(AB+AC=AB'+AC\). Заметим, что по правилу треугольника, если точка \(A\) не лежит на отрезке \(B'C\), то \(AB'+AC>B'C\). Следовательно, наименьшая сумма длин \(AB'+AC\) будет достигаться тогда, когда \(A\in B'C\).


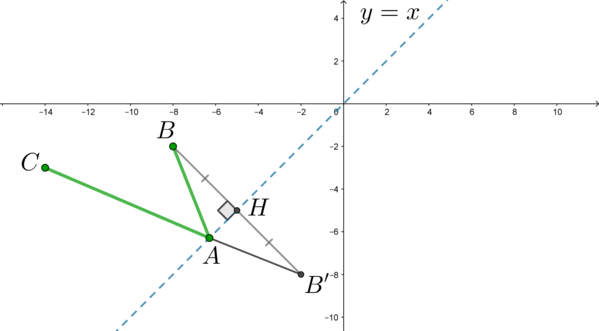
Таким образом, мы идейно поняли, где должна находиться точка \(A\). Теперь осталось найти ее координаты.

1) Найдем координаты точки \(B'\).
Для этого сначала найдем уравнение прямой \(BB'\). Так как \(BB'\perp y=x\), то если уравнение прямой \(BB'\) имеет вид \(y=kx+b\), то \(k\cdot 1=-1\) (произведение угловых коэффициентов двух взаимно перпендикулярных прямых равно \(-1\)). Следовательно, \(y=-x+b\).
Для того, чтобы найти число \(b\), нужно подставить координаты точки \(B\) в уравнение прямой: \[-2=-1\cdot (-8)+b\quad\Leftrightarrow\quad b=-10\] Следовательно, уравнение прямой имеет вид \(y=-x-10\).
Найдем координаты точки \(H\) – это точка пересечения прямых \(y=x\) и \(y=-x-10\): \[\begin{cases} y=x\\ y=-x-10\end{cases}\quad\Leftrightarrow\quad x=y=-5\quad\Rightarrow\quad H(-5;-5)\] \(H\) – середина отрезка \(BB'\). Значит, если координаты точки \(B'\) равны \((x_0;y_0)\), то \[\begin{cases} -5=\dfrac{-8+x_0}2\\[2ex] -5=\dfrac{-2+y_0}2\end{cases}\quad\Leftrightarrow\quad \begin{cases} x_0=-2\\ y_0=-8\end{cases}\] Таким образом, \(B'(-2;-8)\).

2) Найдем уравнение прямой \(B'C\). Если уравнение этой прямой в общем виде выглядит как \(y=mx+n\), то \[\begin{cases} -8=-2m+n\\ -3=-14m+n\end{cases}\quad\Leftrightarrow\quad \begin{cases} m=-\dfrac5{12}\\[2ex] n=-\dfrac{53}6\end{cases}\] Следовательно, \(y=-\frac5{12}x-\frac{53}6\). Теперь можно найти координаты точки \(A\) – это точка пересечения прямых \(y=x\) и \(B'C\): \[\begin{cases} y=x\\[2ex] y=-\frac5{12}x-\frac{53}6\end{cases} \quad\Leftrightarrow\quad x=y=-\dfrac{106}{17}\]

3) Теперь можно найти значение параметра \(a\). \[13a=AB'+AC=13\quad\Rightarrow\quad a=1\]

Чем хорош этот способ? Во-первых, он более изящный. Во-вторых, в ходе решения мы сталкивались только с линейными уравнениями, которые решать намного проще.

Ответ:

\(a=1\)

Изобразим график первого уравнения. Для этого рассмотрим случаи:

1) \(x^2-2x\geqslant 0\), \(y^2-2y\geqslant 0\). Тогда уравнение примет вид \[x^2+x^2-2x=y^2+y^2-2y\quad\Leftrightarrow\quad x^2-y^2-(x-y)=0\quad\Leftrightarrow\quad (x-y)(x+y-1)=0\quad\Leftrightarrow\quad \left[\begin{gathered}\begin{aligned} &y=x\\ &y=1-x\end{aligned}\end{gathered}\right.\] Тогда в этом случае получаем такой график:

2) \(x^2-2x\leqslant 0\), \(y^2-2y\leqslant 0\). Тогда: \[x^2+2x-x^2=y^2+2y-y^2\quad\Leftrightarrow\quad y=x\] Значит, график для первых двух случаев будет выглядеть уже так:

3) \(x^2-2x\geqslant 0\), \(y^2-2y\leqslant 0\). Тогда уравнение примет вид: \[x^2+x^2-2x=y^2-y^2+2y\quad\Leftrightarrow\quad y=x^2-x\] Следовательно, добавится еще:

4) \(x^2-2x\leqslant 0\), \(y^2-2y\geqslant 0\). Тогда имеем: \[x=y^2-y\] Графиком будет являться такая же парабола, как и в п.3, только с поменявшимися осями:

Графиком \(x+y=a\) при каждом фиксированном \(a\) является прямая \(y=-x+a\), то есть прямая, параллельная \(y=-x\) (а также параллельная части прямой \(y=1-x\) из п. 1).
Для того, чтобы система имела более двух решений, нужно, чтобы прямая \(y=-x+a\) находилась в положениях от (1) (не включительно) до (2) (включительно):

Действительно, когда прямая находится в положении (2), то система будет иметь бесконечное множество решений (а именно, часть прямой \(y=1-x\) при \(x\in (-\infty;-1]\cup[2;+\infty)\), а также точка \((0,5;0,5)\)); когда прямая находится между (1) и (2), то система будет иметь 3 решения; когда прямая находится в положении (1), то система будет иметь одно решение: \(x=0, y=0\).
Прямая \(y=-x+a\) находится в положении (1) при \(a=0\), в положении (2) – при \(a=1\), следовательно, \[a\in (0;1]\]

Ответ:

\(a\in (0;1]\)

Изобразим график первого уравнения. Для этого рассмотрим следующие случаи:

1) \(x^2-1\geqslant 0\), \(y^2-1\geqslant 0\). Тогда уравнение примет вид \[x^2-1+2x-x^2=y^2-1+2y-y^2\quad\Leftrightarrow\quad x=y\] Следовательно, в части плоскости, задающейся условиями \(|x|\geqslant 1\), \(|y|\geqslant 1\), графиком будет часть прямой \(y=x\):

2) \(x^2-1\leqslant 0\), \(y^2-1\geqslant 0\). Тогда уравнение примет вид: \[1-x^2+2x-x^2=y^2-1+2y-y^2\quad\Leftrightarrow\quad y=-x^2+x+1\] Следовательно, в части плоскости, задающейся условиями \(|x|\leqslant 1, |y|\geqslant 1\), графиком будет часть параболы \(y=-x^2+x+1\):

3) \(x^2-1\leqslant 0\), \(y^2-1\leqslant 0\): \[1-x^2+2x-x^2=1-y^2+2y-y^2\quad\Leftrightarrow\quad 1-2y+y^2-x^2=1-2x+x^2-y^2\quad\Leftrightarrow\quad (1-y)^2-x^2=(1-x)^2-y^2\quad\Leftrightarrow\] \[\Leftrightarrow\quad (1-y-x)(1-y+x)=(1-x-y)(1-x+y)\quad\Leftrightarrow\quad (1-y-x)(1-y+x-1+x-y)=0\quad\Leftrightarrow\quad \left[\begin{gathered}\begin{aligned} &y=1-x\\ &y=x\end{aligned}\end{gathered}\right.\] Следовательно, добавится еще такой кусок графика:

4) \(x^2-1\geqslant 0\), \(y^2-1\leqslant 0\). Тогда имеем \[x=-y^2+y+1\] Графиком будет та же парабола, что и в п. 2, если поменять оси местами.   Таким образом, окончательный график первого уравнения будет выглядеть так:

Графиком \(x+y=a\) при каждом фиксированном \(a\) является прямая \(y=-x+a\), то есть прямая, параллельная \(y=-x\) (а также параллельная части прямой \(y=1-x\) из п. 3).
Для того, чтобы система имела более двух решений, нужно, чтобы прямая \(y=-x+a\) находилась в положениях от (1) (включительно) до (2) (не включительно):

Действительно, когда прямая находится в положении (1), то система будет иметь бесконечное множество решений (а именно, часть прямой \(y=1-x\) при \(x\in [0;1]\)); когда прямая находится между (1) и (2), то система будет иметь 3 решения; когда прямая находится в положении (2), то система будет иметь одно решение: \(x=1, y=1\).
Прямая \(y=-x+a\) находится в положении (1) при \(a=1\), в положении (2) – при \(a=2\), следовательно, \[a\in [1;2)\]

Ответ:

\([1;2)\)