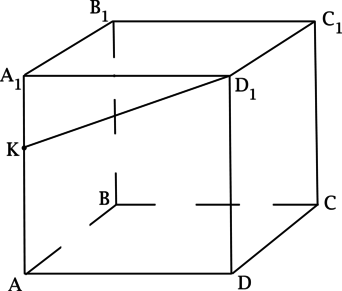
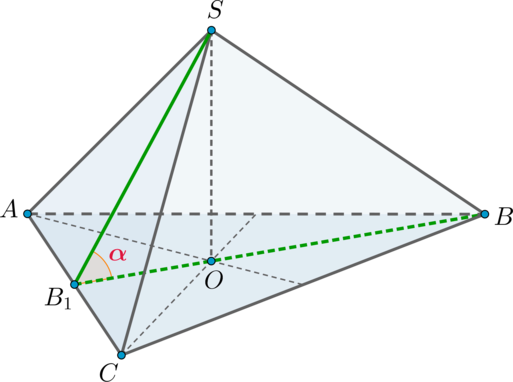
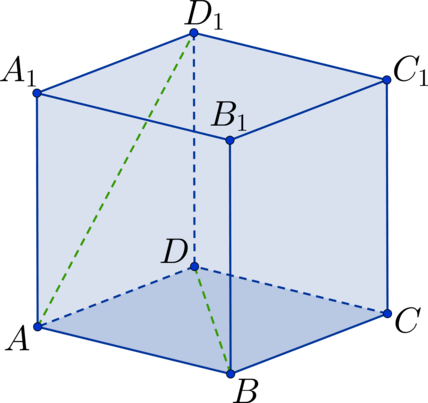
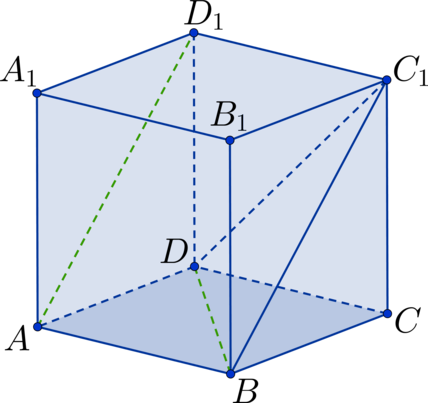
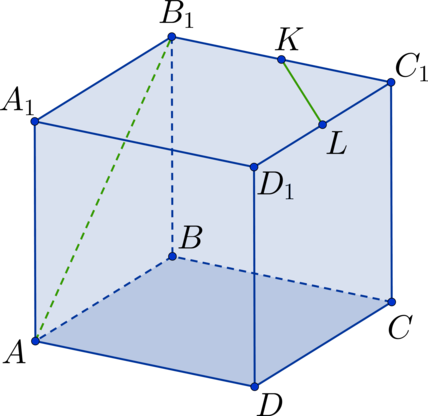
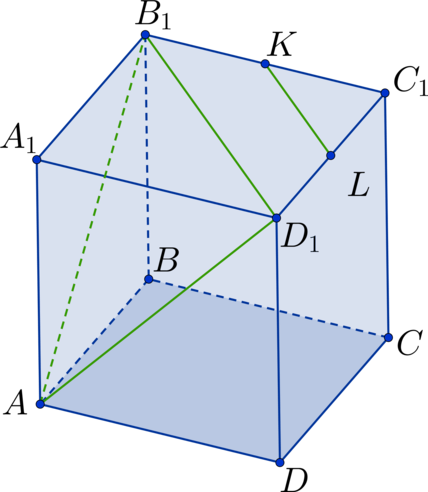
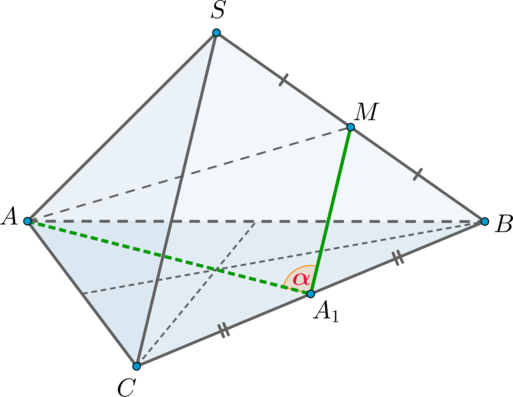
Каждому школьнику, который готовится к ЕГЭ по математике, будет полезно повторить тему «Нахождение угла между прямыми». Как показывает статистика, при сдаче аттестационного испытания задачи по данному разделу стереометрии вызывают трудности у большого количества учащихся. При этом задания, требующие найти угол между прямыми, встречаются в ЕГЭ как базового, так и профильного уровня. Это значит, что уметь их решать должны все.
Основные моменты
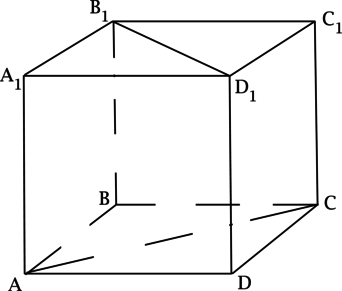
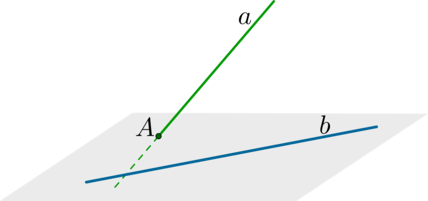
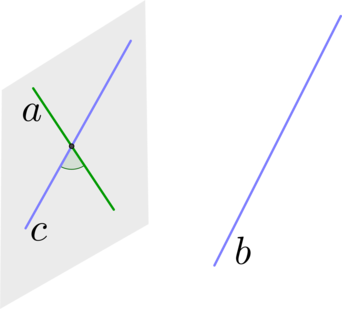
В пространстве существует 4 типа взаимного расположения прямых. Они могут совпадать, пересекаться, быть параллельными или скрещивающимися. Угол между ними может быть острым или прямым.
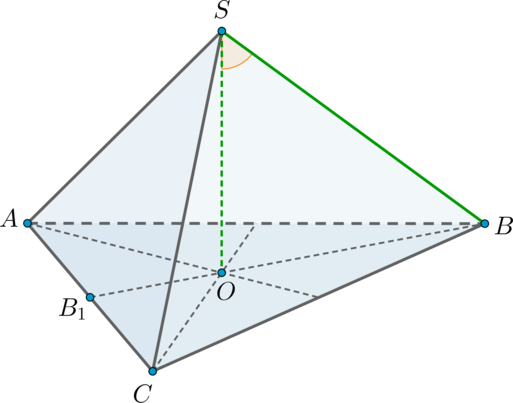
Для нахождения угла между прямыми в ЕГЭ или, например, в решении задач по теореме о трех перпендикулярах, школьники Москвы и других городов могут использовать несколько способов решения задач по данному разделу стереометрии. Выполнить задание можно путем классических построений. Для этого стоит выучить основные аксиомы и теоремы стереометрии. Школьнику нужно уметь логически выстраивать рассуждение и создавать чертежи, для того чтобы привести задание к планиметрической задаче.
Также можно использовать векторно-координатный метод, применяя простые формулы, правила и алгоритмы. Главное в этом случае — правильно выполнить все вычисления. Отточить свои навыки решения задач по стереометрии и другим разделам школьного курса вам поможет образовательный проект «Школково».