Четные и нечетные функции

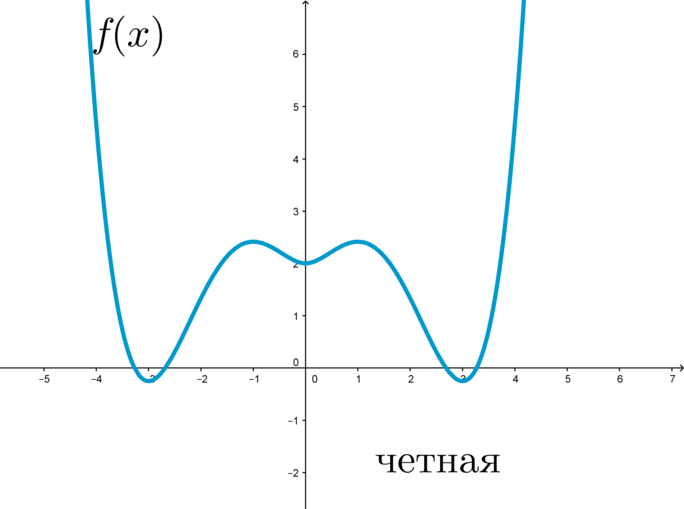
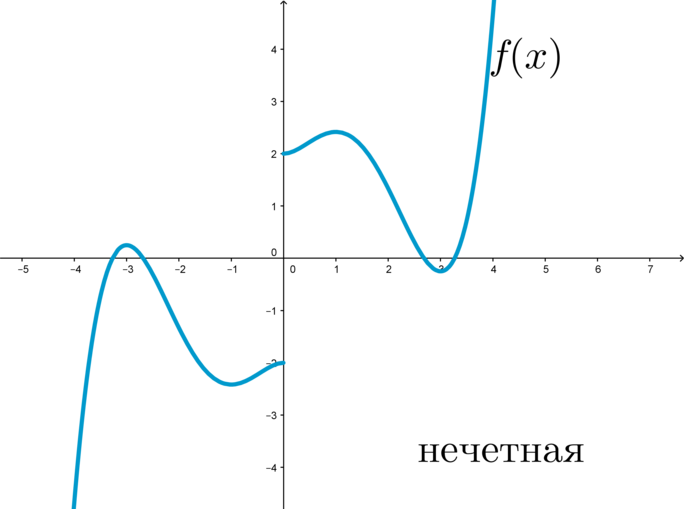
Заметим, что так как \(x^2\) и \(\cos x\) — четные функции, то если уравнение будет иметь корень \(x_0\), оно также будет иметь и корень \(-x_0\).
Действительно, пусть \(x_0\) – корень, то есть равенство \(2x_0^2+a\mathrm{tg}\,(\cos x_0)+a^2=0\) верно. Подставим \(-x_0\): \(2 (-x_0)^2+a\mathrm{tg}\,(\cos(-x_0))+a^2=2x_0^2+a\mathrm{tg}\,(\cos x_0)+a^2=0\).

Таким образом, если \(x_0\ne 0\), то уравнение уже будет иметь как минимум два корня. Следовательно, \(x_0=0\). Тогда:

\[2\cdot 0+a\mathrm{tg}\,(\cos 0)+a^2=0 \quad \Rightarrow \quad a^2+a\mathrm{tg}\,1=0 \quad \Rightarrow \quad \left[ \begin{gathered}\begin{aligned} &a=0\\ &a=-\mathrm{tg}\,1 \end{aligned} \end{gathered}\right.\]

Мы получили два значения параметра \(a\). Заметим, что мы использовали то, что \(x=0\) точно является корнем исходного уравнения. Но мы нигде не использовали то, что он единственный. Следовательно, нужно подставить получившиеся значения параметра \(a\) в исходное уравнение и проверить, при каких именно \(a\) корень \(x=0\) действительно будет единственным.

1) Если \(a=0\), то уравнение примет вид \(2x^2=0\). Очевидно, что это уравнение имеет лишь один корень \(x=0\). Следовательно, значение \(a=0\) нам подходит.

2) Если \(a=-\mathrm{tg}\,1\), то уравнение примет вид \[2x^2-\mathrm{tg}\,1\cdot \mathrm{tg}\,(\cos x)+\mathrm{tg}^2\,1=0\] Перепишем уравнение в виде \[2x^2+\mathrm{tg}^2\,1=\mathrm{tg}\,1\cdot \mathrm{tg}\,(\cos x)\qquad (*)\] Так как \(-1\leqslant \cos x\leqslant 1\), то \(-\mathrm{tg}\,1\leqslant \mathrm{tg}\,(\cos x)\leqslant \mathrm{tg}\,1\). Следовательно, значения правой части уравнения (*) принадлежат отрезку \([-\mathrm{tg}^2\,1; \mathrm{tg}^2\,1]\).

Так как \(x^2\geqslant 0\), то левая часть уравнения (*) больше или равна \(0+ \mathrm{tg}^2\,1\).

Таким образом, равенство (*) может выполняться только тогда, когда обе части уравнения равны \(\mathrm{tg}^2\,1\). А это значит, что \[\begin{cases} 2x^2+\mathrm{tg}^2\,1=\mathrm{tg}^2\,1 \\ \mathrm{tg}\,1\cdot \mathrm{tg}\,(\cos x)=\mathrm{tg}^2\,1 \end{cases} \quad\Leftrightarrow\quad \begin{cases} x=0\\ \mathrm{tg}\,(\cos x)=\mathrm{tg}\,1 \end{cases}\quad\Leftrightarrow\quad x=0\] Следовательно, значение \(a=-\mathrm{tg}\,1\) нам подходит.

Ответ:

\(a\in \{-\mathrm{tg}\,1;0\}\)

Если график функции симметричен относительно начала координат, то такая функция является нечетной, то есть выполнено \(f(-x)=-f(x)\) для любого \(x\) из области определения функции. Таким образом, требуется найти те значения параметра, при которых выполнено \(f(-x)=-f(x).\)

\[\begin{aligned} &3\mathrm{tg}\,\left(-\dfrac{ax}5\right)+2\sin \dfrac{8\pi a+3x}4= -\left(3\mathrm{tg}\,\left(\dfrac{ax}5\right)+2\sin \dfrac{8\pi a-3x}4\right)\quad \Rightarrow\quad -3\mathrm{tg}\,\dfrac{ax}5+2\sin \dfrac{8\pi a+3x}4= -\left(3\mathrm{tg}\,\left(\dfrac{ax}5\right)+2\sin \dfrac{8\pi a-3x}4\right) \quad \Rightarrow\\[3ex] \Rightarrow\quad &\sin \dfrac{8\pi a+3x}4+\sin \dfrac{8\pi a-3x}4=0 \quad \Rightarrow \quad2\sin \dfrac12\left(\dfrac{8\pi a+3x}4+\dfrac{8\pi a-3x}4\right)\cdot \cos \dfrac12 \left(\dfrac{8\pi a+3x}4-\dfrac{8\pi a-3x}4\right)=0 \quad \Rightarrow\quad \sin (2\pi a)\cdot \cos \frac34 x=0 \end{aligned}\]

Последнее уравнение должно быть выполнено для всех \(x\) из области определения \(f(x)\), следовательно, \(\sin(2\pi a)=0 \Rightarrow a=\dfrac n2, n\in\mathbb{Z}\).

Ответ:

\(\dfrac n2, n\in\mathbb{Z}\)

Так как \(f(x)\) – четная функция, то ее график симметричен относительно оси ординат, следовательно, при \(-\dfrac83\leqslant x\leqslant 0\) \(f(x)=ax^2\). Таким образом, при \(-\dfrac83\leqslant x\leqslant \dfrac83\), а это отрезок длиной \(\dfrac{16}3\), функция \(f(x)=ax^2\).

1) Пусть \(a>0\). Тогда график функции \(f(x)\) будет выглядеть следующим образом:

Тогда для того, чтобы уравнение имело 4 решения, нужно, чтобы график \(g(x)=|a+2|\cdot \sqrt[3]x\) проходил через точку \(A\):

Следовательно, \[\dfrac{64}9a=|a+2|\cdot \sqrt[3]8 \quad\Leftrightarrow\quad \left[\begin{gathered}\begin{aligned} &9(a+2)=32a\\ &9(a+2)=-32a \end{aligned} \end{gathered}\right. \quad\Leftrightarrow\quad \left[\begin{gathered}\begin{aligned} &a=\dfrac{18}{23}\\[2ex] &a=-\dfrac{18}{41} \end{aligned} \end{gathered}\right.\] Так как \(a>0\), то подходит \(a=\dfrac{18}{23}\).

2) Пусть \(a<0\). Тогда картинка окажется симметричной относительно начала координат:

Нужно, чтобы график \(g(x)\) прошел через точку \(B\): \[\dfrac{64}9a=|a+2|\cdot \sqrt[3]{-8} \quad\Leftrightarrow\quad \left[\begin{gathered}\begin{aligned} &a=\dfrac{18}{23}\\[2ex] &a=-\dfrac{18}{41} \end{aligned} \end{gathered}\right.\] Так как \(a<0\), то подходит \(a=-\dfrac{18}{41}\).

3) Случай, когда \(a=0\), не подходит, так как тогда \(f(x)=0\) при всех \(x\), \(g(x)=2\sqrt[3]x\) и уравнение будет иметь только 1 корень.

Ответ:

\(a\in \left\{-\dfrac{18}{41};\dfrac{18}{23}\right\}\)

Перепишем уравнение в виде \[7\sqrt{2x^2+49}=3|x-7a|-6|x|-a^2+7a\] и рассмотрим две функции: \(g(x)=7\sqrt{2x^2+49}\) и \(f(x)=3|x-7a|-6|x|-a^2+7a\).
Функция \(g(x)\) является четной, имеет точку минимума \(x=0\) (причем \(g(0)=49\)).
Функция \(f(x)\) при \(x>0\) является убывающей, а при \(x<0\) – возрастающей, следовательно, \(x=0\) – точка максимума.
Действительно, при \(x>0\) второй модуль раскроется положительно (\(|x|=x\)), следовательно, вне зависимости от того, как раскроется первый модуль, \(f(x)\) будет равно \(kx+A\), где \(A\) – выражение от \(a\), а \(k\) равно либо \(-9\), либо \(-3\). При \(x<0\) наоборот: второй модуль раскроется отрицательно и \(f(x)=kx+A\), где \(k\) равно либо \(3\), либо \(9\).
Найдем значение \(f\) в точке максимума: \[f(0)=-a^2+7a+21|a|\]


Для того, чтобы уравнение имело хотя бы одно решение, нужно, чтобы графики функций \(f\) и \(g\) имели хотя бы одну точку пересечения. Следовательно, нужно: \[f(0)\geqslant g(0) \quad\Rightarrow\quad -a^2+7a+21|a|\geqslant 49 \quad\Leftrightarrow\quad \left[ \begin{gathered} \begin{aligned} &\begin{cases} a>0\\ a^2-28a+49\leqslant 0 \end{cases}\\ &\begin{cases} a<0\\ a^2+14a+49\leqslant 0 \end{cases}\\ &\begin{cases} a=0\\ 0\geqslant 49\end{cases} \end{aligned} \end{gathered}\right.\] Решая данную совокупность систем, получим ответ: \[a\in \{-7\}\cup [14-7\sqrt3;14+7\sqrt3]\]

Ответ:

\(a\in \{-7\}\cup[14-7\sqrt3;14+7\sqrt3]\)

Сделаем замену \((\sqrt2)^{x^3-3x^2+4}=t\), \(t>0\). Тогда уравнение примет вид \[t^2+(a-10)t+12-a=0\quad (*)\] Будем постепенно выписывать условия, при которых исходное уравнение будет иметь шесть решений.
Заметим, что квадратное уравнение \((*)\) может максимум иметь два решения. Любое кубическое уравнение \(Ax^3+Bx^2+Cx+D=0\) может иметь не более трех решений. Следовательно, если уравнение \((*)\) имеет два различных решения (положительных!, так как \(t\) должно быть больше нуля) \(t_1\) и \(t_2\), то, сделав обратную замену, мы получим: \[\left[\begin{gathered}\begin{aligned} &(\sqrt2)^{x^3-3x^2+4}=t_1\\[2ex] &(\sqrt2)^{x^3-3x^2+4}=t_2\end{aligned}\end{gathered}\right.\] Так как любое положительное число можно представить как \(\sqrt2\) в какой-то степени, например, \(t_1=(\sqrt2)^{\log_{\sqrt2} t_1}\), то первое уравнение совокупности перепишется в виде \[x^3-3x^2+4=\log_{\sqrt2} t_1\] Как мы уже говорили, любое кубическое уравнение имеет не более трех решений, следовательно, каждое уравнение из совокупности будет иметь не более трех решений. А значит и вся совокупность будет иметь не более шести решений.
Значит, чтобы исходное уравнение имело шесть решений, квадратное уравнение \((*)\) должно иметь два различных решения, а каждое полученное кубическое уравнение (из совокупности) должно иметь три различных решения (причем ни одно решение одного уравнения не должно совпадать с каким-либо решением второго!)
Очевидно, что если квадратное уравнение \((*)\) будет иметь одно решение, то мы никак не получим шесть решений у исходного уравнения.

Таким образом, план решения становится ясен. Давайте по пунктам выпишем условия, которые должны выполняться.

1) Чтобы уравнение \((*)\) имело два различных решения, его дискриминант должен быть положительным: \[D=a^2-16a+52>0\quad\Leftrightarrow\quad a\in (-\infty;8-2\sqrt3)\cup(8+2\sqrt3;+\infty)\]

2) Также нужно, чтобы оба корня были положительными (так как \(t>0\)). Если произведение двух корней положительное и сумма их положительная, то и сами корни будут положительными. Следовательно, нужно: \[\begin{cases} 12-a>0\\-(a-10)>0\end{cases}\quad\Leftrightarrow\quad a<10\]

Таким образом, мы уже обеспечили себе два различных положительных корня \(t_1\) и \(t_2\).

3) Давайте посмотрим на такое уравнение \[x^3-3x^2+4=\log_{\sqrt2} t\] При каких \(t\) оно будет иметь три различных решения?
Рассмотрим функцию \(f(x)=x^3-3x^2+4\).
Можно разложить на множители: \[x^3-3x^2+4=x^3+x^2-4x^2+4=x^2(x+1)-4(x+1)(x-1)=(x+1)(x-2)^2\] Следовательно, ее нули: \(x=-1;2\).
Если найти производную \(f'(x)=3x^2-6x\), то мы получим две точки экстремума \(x_{max}=0, x_{min}=2\).
Следовательно, график выглядит так:

Мы видим, что любая горизонтальная прямая \(y=k\), где \(0<k<4\), пересекает график в трех точках. При всех остальных значениях \(k\) будет меньше трех точек пересечения. Следовательно, для того, чтобы уравнение \(x^3-3x^2+4=\log_{\sqrt2} t\) имело три различных решения, нужно, чтобы \(0<\log_ {\sqrt2}t<4\).
Таким образом, нужно: \[\begin{cases} 0<\log_{\sqrt2}t_1<4\\ 0<\log_{\sqrt2}t_2<4\end{cases}\qquad (**)\] Давайте также сразу заметим, что если числа \(t_1\) и \(t_2\) различны, то и числа \(\log_{\sqrt2}t_1\) и \(\log_{\sqrt2}t_2\) будут различны, значит, и уравнения \(x^3-3x^2+4=\log_{\sqrt2} t_1\) и \(x^3-3x^2+4=\log_{\sqrt2} t_2\) будут иметь несовпадающие между собой корни.
Систему \((**)\) можно переписать так: \[\begin{cases} 1<t_1<4\\ 1<t_2<4\end{cases}\]

Таким образом, мы определили, что оба корня уравнения \((*)\) должны лежать в интервале \((1;4)\). Как записать это условие?
В явном виде выписывать корни мы не будем.
Рассмотрим функцию \(g(t)=t^2+(a-10)t+12-a\). Ее график – парабола с ветвями вверх, которая имеет две точки пересечения с осью абсцисс (это условие мы записали в пункте 1)). Как должен выглядеть ее график, чтобы точки пересечения с осью абсцисс были в интервале \((1;4)\)? Так:

Во-первых, значения \(g(1)\) и \(g(4)\) функции в точках \(1\) и \(4\) должны быть положительными, во-вторых, вершина параболы \(t_0\) должна также находиться в интервале \((1;4)\). Следовательно, можно записать систему: \[\begin{cases} 1+a-10+12-a>0\\[1ex] 4^2+(a-10)\cdot 4+12-a>0\\[2ex] 1<\dfrac{-(a-10)}2<4\end{cases}\quad\Leftrightarrow\quad 4<a<8\]

Таким образом, нам нужно пересечь значения параметра \(a\), найденные в 1-ом, 2-ом и 3-ем пунктах, и мы получим ответ: \[\begin{cases} a\in (-\infty;8-2\sqrt3)\cup(8+2\sqrt3;+\infty)\\ a<10\\ 4<a<8\end{cases}\quad\Leftrightarrow\quad 4<a<8-2\sqrt3\]

Ответ:

\((4;8-2\sqrt3)\)

Заметим, что данное уравнение при любых значениях \(a\) всегда имеет как минимум один корень \(x=0\). Значит, для выполнения условия задачи нужно, чтобы уравнение \[25x^4+25(a-1)x^2-4(a-7)=0 \qquad (*)\]

имело четыре различных корня, отличных от нуля, представляющих вместе с \(x=0\) арифметическую прогрессию.

Заметим, что функция \(y=25x^4+25(a-1)x^2-4(a-7)\) является четной, значит, если \(x_0\) является корнем уравнения \((*)\), то и \(-x_0\) будет являться его корнем. Тогда необходимо, чтобы корнями этого уравнения были упорядоченные по возрастанию числа: \(-2d, -d, d, 2d\) (тогда \(d>0\)). Именно тогда данные пять чисел будут образовывать арифметическую прогрессию (с разностью \(d\)).

Чтобы этими корнями являлись числа \(-2d, -d, d, 2d\), нужно, чтобы числа \(d^{\,2}, 4d^{\,2}\) являлись корнями уравнения \(25t^2+25(a-1)t-4(a-7)=0\). Тогда по теореме Виета:

\[\begin{cases} -\dfrac{4(a-7)}{25}=d^{\,2}\cdot 4d^{\,2}\\[4pt] -\dfrac{25(a-1)}{25}=d^{\,2}+4d^{\,2} \end{cases} \quad \Rightarrow \quad \begin{cases} d^{\,4}=\dfrac{7-a}{25}\\ \dfrac{7-a}{25}=\left(\dfrac{1-a}{5}\right)^2 \end{cases} \quad \Rightarrow \quad \left[\begin{gathered}\begin{aligned} &a=-2\\&a=3 \end{aligned} \end{gathered} \right.\]

Причем при \(a=-2\) \(d=\pm \sqrt{\frac35}\), а при \(a=3\) \(d\in \varnothing\). Значит, подходит значение \(a=-2\) и \(d=\sqrt{\frac35}\) (т.к. должно быть \(d>0\)).

Ответ:

\(a\in \{-2\}\)

Перепишем уравнение в виде \[13|x|-2|5x+12a|=20a-a^2-2^{x^2+2}\] и рассмотрим две функции: \(g(x)=20a-a^2-2^{x^2+2}\) и \(f(x)=13|x|-2|5x+12a|\).
Функция \(g(x)\) имеет точку максимума \(x=0\) (причем \(g_{\text{верш}}=g(0)=-a^2+20a-4\)):
\(g'(x)=-2^{x^2+2}\cdot \ln 2\cdot 2x\). Ноль производной: \(x=0\). При \(x<0\) имеем: \(g'>0\), при \(x>0\): \(g'<0\).
Функция \(f(x)\) при \(x>0\) является возрастающей, а при \(x<0\) – убывающей, следовательно, \(x=0\) – точка минимума.
Действительно, при \(x>0\) первый модуль раскроется положительно (\(|x|=x\)), следовательно, вне зависимости от того, как раскроется второй модуль, \(f(x)\) будет равно \(kx+A\), где \(A\) – выражение от \(a\), а \(k\) равно либо \(13-10=3\), либо \(13+10=23\). При \(x<0\) наоборот: первый модуль раскроется отрицательно и \(f(x)=kx+A\), где \(k\) равно либо \(-3\), либо \(-23\).
Найдем значение \(f\) в точке минимума: \[f_{\text{верш}}=f(0)=-24|a|\]


Для того, чтобы уравнение имело хотя бы одно решение, нужно, чтобы графики функций \(f\) и \(g\) имели хотя бы одну точку пересечения. Следовательно, нужно: \[f(0)\leqslant g(0) \quad\Rightarrow\quad a^2-20a+4\leqslant 24|a| \quad\Leftrightarrow\quad \left[ \begin{gathered} \begin{aligned} &\begin{cases} a\geqslant 0\\ a^2-44a+4\leqslant 0 \end{cases}\\ &\begin{cases} a<0\\ a^2+4a+4\leqslant 0 \end{cases} \end{aligned} \end{gathered}\right.\] Решая данную совокупность систем, получим ответ: \[a\in \{-2\}\cup[22-4\sqrt{30};22+4\sqrt{30}]\]

Ответ:

\(a\in \{-2\}\cup[22-4\sqrt{30};22+4\sqrt{30}]\)