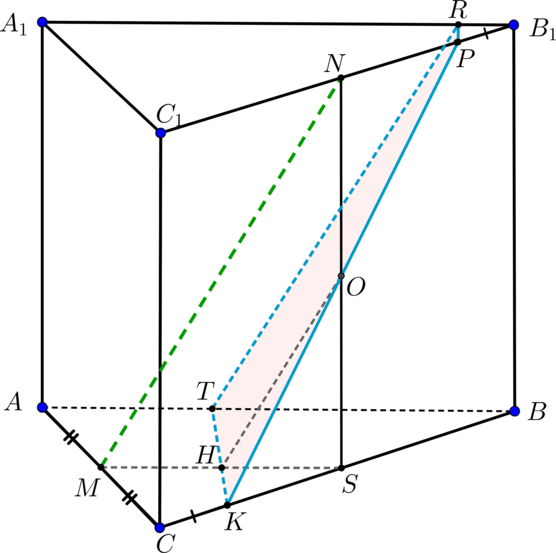
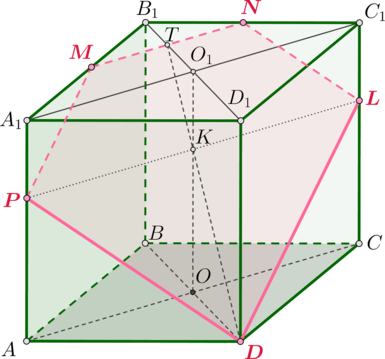
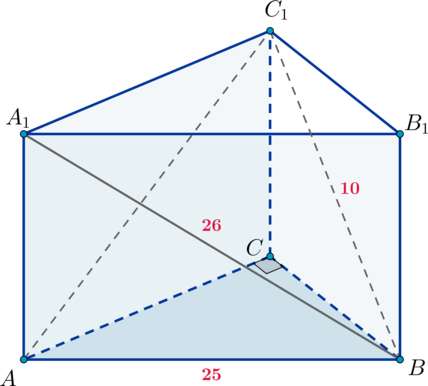
Основанием прямой треугольной призмы \(ABCA_1B_1C_1\) является прямоугольный треугольник \(ABC\), причем \(\angle C=90^\circ\). Диагонали боковых граней \(AA_1B_1B\) и \(BB_1C_1C\) равны соответственно \(26\) и \(10\), \(AB=25\).
а) Докажите, что \(\triangle BA_1C_1\) – прямоугольный.
б) Найдите объем пирамиды \(AA_1C_1B\).
а) Так как \(BB_1\perp (A_1B_1C_1)\), \(B_1C_1\perp A_1C_1\), то по теореме о трех перпендикулярах \(BC_1\perp A_1C_1\) (как наклонная). Следовательно, \(\triangle A_1C_1B\) – прямоугольный.
б) Заметим, что \(BC\perp AC\) и \(BC\perp CC_1\), следовательно, по признаку \(BC\perp (AA_1C_1)\). Следовательно, \(BC\) – высота пирамиды \(BAA_1C_1\) с основанием \(AA_1C_1\).
Так как \(\triangle AA_1C_1\) прямоугольный, то \[V_{BAA_1C_1}=\dfrac{\frac12\cdot AA_1\cdot A_1C_1\cdot BC}3\] По теореме Пифагора \[\begin{aligned}
&A_1C_1=\sqrt{26^2-10^2}=\sqrt{16\cdot 36}=24\\[1ex]
&AA_1=\sqrt{26^2-25^2}=\sqrt{1\cdot 51}=\sqrt{51}\\[1ex]
&BC=\sqrt{10^2-51}=\sqrt{49}=7 \end{aligned}\] Тогда \[V_{BAA_1C_1}=\dfrac{\frac12\cdot 24\cdot \sqrt{51}\cdot 7}3=28\sqrt{51}\]
Ответ:
б) \(28\sqrt{51}\)