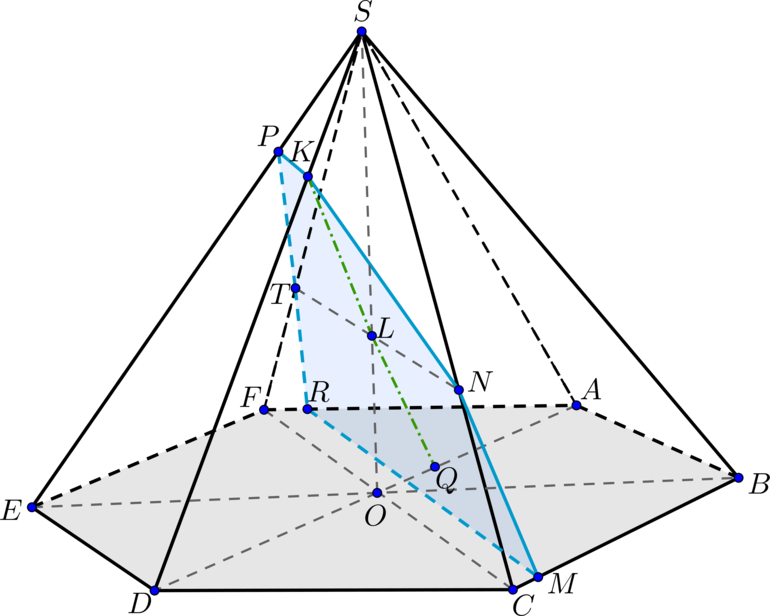
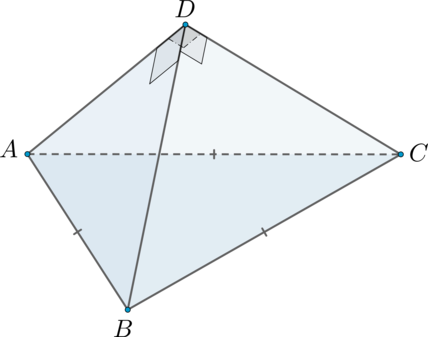
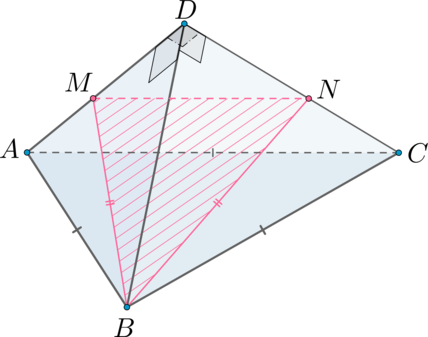
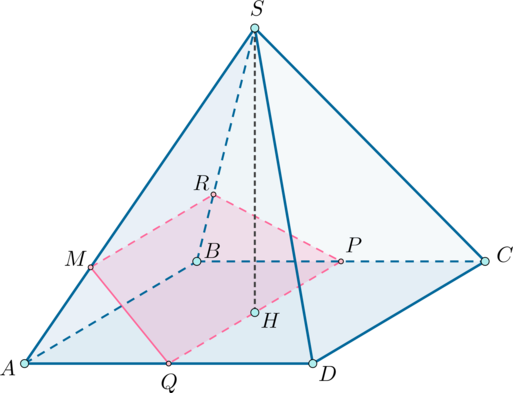
В основании пирамиды \(SABCD\) лежит ромб \(ABCD\), сторона которого равна \(8\), а угол при вершине \(A\) равен \(60^\circ\). Известно, что \(SA=15\), \(SC=\sqrt{33}\), и, кроме того, что \(SB=SD\).
а) Докажите, что \(SC\) – высота пирамиды.
б) Найдите угол между плоскостью \(ASC\) и ребром \(SB\).
(Задача от подписчиков)
а) Рассмотрим основание \(ABCD\). Так как \(\angle A=60^\circ\), то \(\triangle BCD\) равносторонний, следовательно, \(BD=BC=8\). Тогда \(BO=4\), где \(O\) – точка пересечения диагоналей ромба. Тогда по теореме Пифагора \(OC=4\sqrt3\), следовательно, \(AC=8\sqrt3\).
По обратной теореме Пифагора, так как \(AS^2=AC^2+SC^2\), треугольник \(ASC\) является прямоугольным с прямым углом \(SCA\). Следовательно, \(SC\perp AC\).
Заметим, что \(\triangle SCD=\triangle SCB\) по трем сторонам. Следовательно, \(\angle SCD=\angle SCB\).
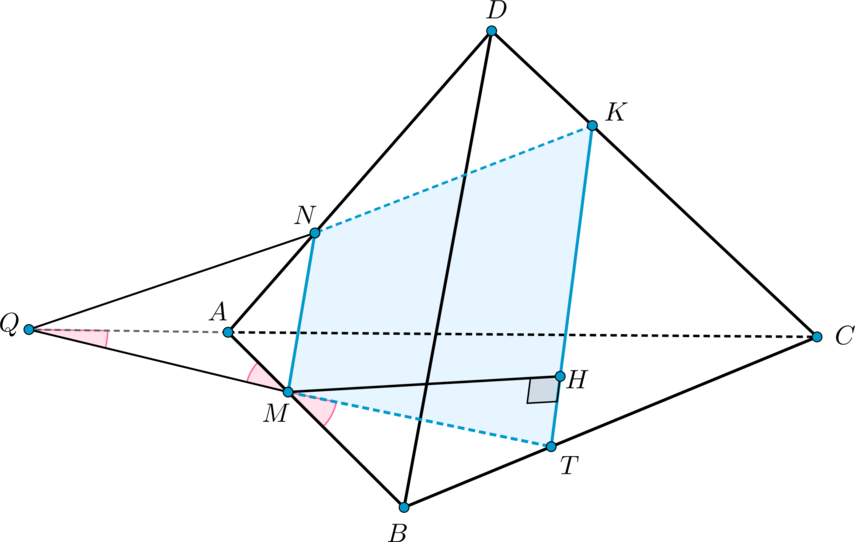
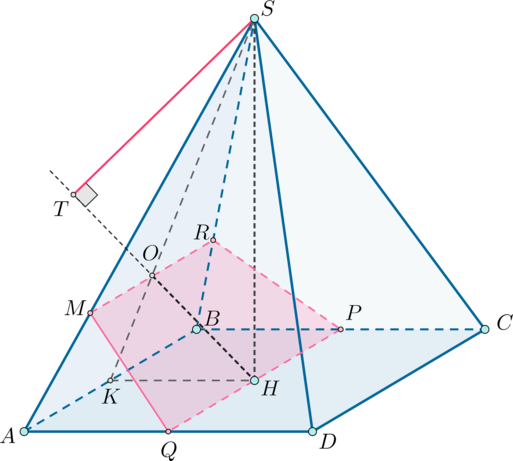
Предположим, что \(SC\) – не высота пирамиды. Тогда опустим высоту \(SH\). Проведем \(HD'\perp CD\) и \(HB'\perp CB\). Тогда по теореме о трех перпендикулярах \(SD'\perp CD\) и \(SB'\perp CB\).
Прямоугольные треугольники \(SCD'\) и \(SCB'\) равны по общему катету \(SC\) и острому углу, следовательно, \(SD'=SB'\). Отсюда следует, что прямоугольные треугольники \(SHD'\) и \(SHB'\) также равны по катету и гипотенузе, следовательно, \(HD'=HB'\). Следовательно, точка \(H\) равноудалена от сторон угла \(C\), значит, лежит на его биссектрисе.
Таким образом, мы доказали, что основание высоты, проведенной из точки \(S\), будет лежать на прямой, содержащей биссектрису угла \(C\) (то есть на прямой \(AC\)).
Но тогда из точки \(S\) проведены две прямые \(SH\) и \(SC\), перпендикулярные \(AC\), что невозможно. Следовательно, точки \(H\) и \(C\) совпадают.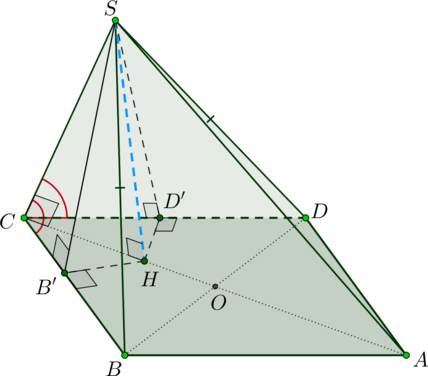
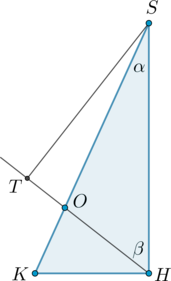
б) Угол между прямой и плоскостью – это угол между прямой и ее проекцией на эту плоскость. Заметим, что \(BO\perp AC\) как диагонали ромба, и \(BO\perp SC\), так как \(SC\) – высота пирамиды. Следовательно, \(BO\perp (ASC)\). Значит, \(SO\) – проекция \(SB\) на плоскость \(ASC\). Таким образом, нужно найти угол \(BSO\). Обозначим его за \(\alpha\).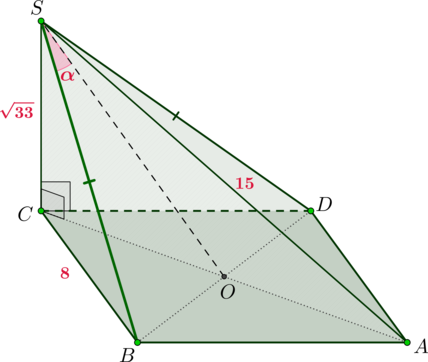
По теореме Пифагора из \(\triangle SCO\): \[SO^2=33+16\cdot 3=81 \quad\Rightarrow\quad SO=9.\] \(BO\) мы находили ранее и оно равно \(4\).
Так как \(\triangle SBO\) прямоугольный (\(\angle O=90^\circ\)), то \[\mathrm{tg}\,\alpha=\dfrac{BO}{SO}=\dfrac{4}{9} \quad\Rightarrow\quad
\alpha=\mathrm{arctg}\,\dfrac49.\]
Ответ:
б) \(\mathrm{arctg}\,\dfrac49\)