Заметим, что вода – это раствор, не содержащий кислоту, то есть содержащий \(0\%\) кислоты.
Пусть \(x\) кг – масса раствора с \(25\)-процентным содержанием кислоты, \(y\) кг – масса раствора с \(95\)-процентным содержанием кислоты. Составим схему, описывающую получение \(40\)-процентного раствора:
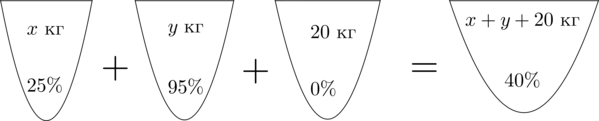
Заметим, что количество кислоты во всех трех растворах равно количеству кислоты в получившемся растворе. Найдем количество кислоты в первом растворе.
Если раствор весит \(x\) кг, а в нем \(25\%\) кислоты, то в килограммах в нем \(\dfrac{25}{100}\cdot x\) кислоты.
Таким же образом можно посчитать количество кислоты в остальных растворах. Получим первое уравнение:
\[\dfrac{25}{100}\cdot x+\dfrac{95}{100}\cdot y+
\dfrac{0}{100}\cdot 20=\dfrac{40}{100}\cdot (x+y+20)\]
Аналогично составим схему, описывающую получение \(50\)-процентного раствора:
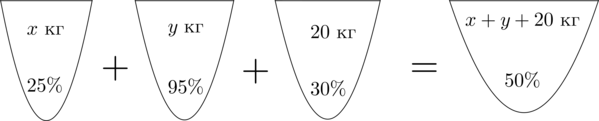
Значит, уравнение, описывающее эту ситуацию, будет выглядеть так:
\[\dfrac{25}{100}\cdot x+\dfrac{95}{100}\cdot y+
\dfrac{30}{100}\cdot 20=\dfrac{50}{100}\cdot (x+y+20)\]
Таким образом, решив систему из полученных двух уравнений, найдем \(x\). Для этого можно умножить оба уравнения на \(100\), чтобы сделать их проще на вид:
\[\begin{cases}
25x+95y+0=40(x+y+20)\\
25x+95y+30\cdot 20=50(x+y+20)
\end{cases}\]
Вычтем из второго уравнения первое и получим новую систему:
\[\begin{aligned} &\begin{cases}
25x+95y=40(x+y+20)\\
30\cdot 20=10(x+y+20)
\end{cases} \quad \Rightarrow \quad \begin{cases}
5x+19y=8(x+y+20)\\
y=40-x \end{cases} \quad \Rightarrow \\[2ex] \Rightarrow \quad
&\begin{cases}
3x-11(40-x)+160=0\\
y=40-x \end{cases} \quad \Rightarrow \quad \begin{cases}
x=20\\y=20\end{cases} \end{aligned}\]
Таким образом, раствора с \(25\%\) кислоты было \(20\) кг.
Ответ: 20





