Выпускники, которые готовятся к сдаче экзамена по математике и рассчитывают на получение достойных баллов, непременно должны справляться с задачами ЕГЭ на нахождение углов, сторон и площадей прямоугольника. Подобные планиметрические задания встречаются в аттестационном испытании каждый год.
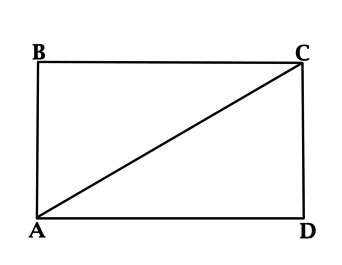
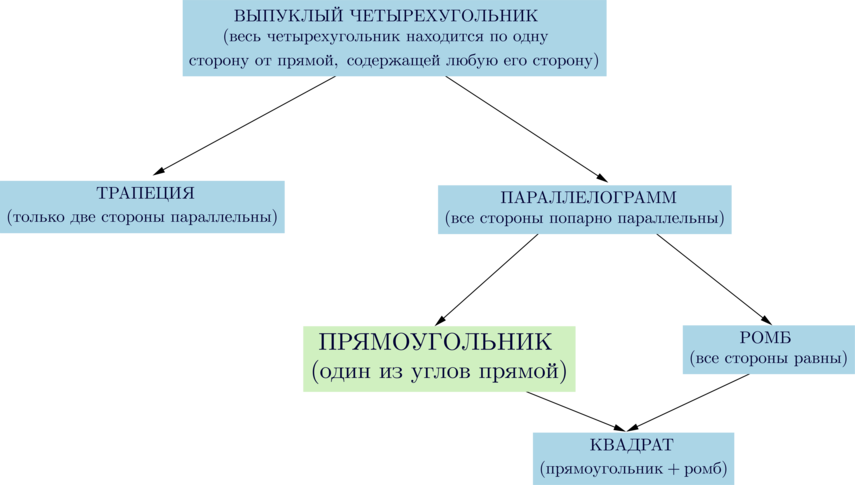
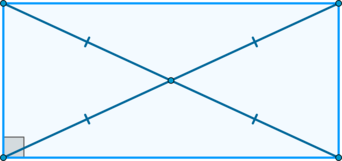
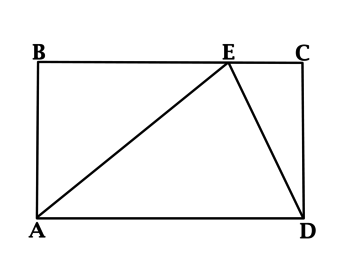
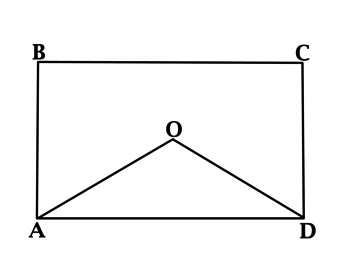
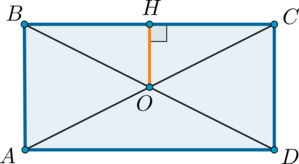
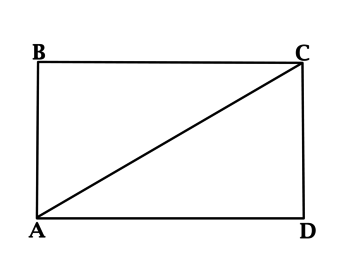
Чтобы успешно решить задачи ЕГЭ по теме «Прямоугольник и его свойства», стоит вспомнить основные понятия из базового школьного курса. При этом рекомендуется следовать определенному алгоритму. Приступая к выполнению заданий ЕГЭ, к примеру, на нахождение сторон прямоугольника или геометрические свойства ромба, сделайте чертеж и отразите на нем все данные, которые известны согласно условию. Затем вспомните относящиеся к ним формулы и теоремы. Применив их, вы сможете найти правильный ответ.
Если задания ЕГЭ по теме «Прямоугольник и его свойства» вызывают у вас затруднения, обратитесь к образовательному порталу «Школково». Здесь вы сможете освежить в памяти базовый теоретический материал и попрактиковаться в выполнении упражнений. Наши специалисты собрали как простые, так и более сложные задания.
Для каждого из них на сайте представлен подробный алгоритм решения.
Оттачивать практический навык школьники могут в режиме онлайн, находясь в любом городе России.