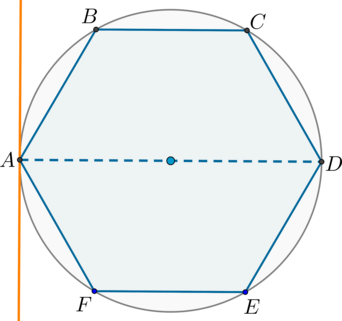
Теме «Правильный шестиугольник и его свойства» в ЕГЭ по математике традиционно отводится сразу несколько заданий. Причем в зависимости от условия от учащегося может требоваться как развернутый, так и краткий ответ. Именно поэтому в процессе подготовки к сдаче аттестационного испытания выпускникам непременно стоит научиться решать задачи на применение свойств этой фигуры, в которых необходимо найти ее стороны, диагонали, радиус окружности со вписанным правильным шестиугольником и т. д.
Восполнить пробелы в знаниях, «прокачать» навыки и улучшить собственные знания по данной теме вам поможет образовательный проект «Школково». Наши специалисты подготовили и изложили весь базовый материал для подготовки к ЕГЭ в максимально доступной форме.
Чтобы школьники могли успешно справляться с задачами по данной теме, мы рекомендуем повторить базовые понятия: каковы свойства правильного шестиугольника, описанного около окружности, как вычисляется его площадь, чему равны его углы и т. д. Весь необходимый материал вы найдете в разделе «Теоретическая справка». Он был разработан нашими сотрудники на основе богатого практического опыта.
Для закрепления полученных знаний предлагаем потренироваться в решении соответствующих задач, а также заданий по теме «Параллелограмм в ЕГЭ». Найти их вы сможете в разделе «Каталог». Для каждого упражнения на сайте представлены алгоритм решения и правильный ответ.
Готовиться к ЕГЭ школьники из Москвы и других городов могут в режиме онлайн. В случае необходимости любое упражнение можно сохранить в разделе «Избранное». В дальнейшем к этому заданию можно будет вернуться и, к примеру, обсудить алгоритм его решения с преподавателем.