Известно, что \[f(x)=\dfrac x{0,2}+\dfrac1{5x}\]
Найдите \(f\left(\dfrac14\right)\).
Подставим \(x=\dfrac14\): \[f\left(\dfrac14\right)=\dfrac{\frac14}{\frac15}+\dfrac1{\frac54}= \dfrac54+\dfrac45=\dfrac{41}{20}=2,05\]
Ответ:
2,05
ДВИ в МГУ им. М. В. Ломоносова
Известно, что \[f(x)=\dfrac x{0,2}+\dfrac1{5x}\]
Найдите \(f\left(\dfrac14\right)\).
Подставим \(x=\dfrac14\): \[f\left(\dfrac14\right)=\dfrac{\frac14}{\frac15}+\dfrac1{\frac54}= \dfrac54+\dfrac45=\dfrac{41}{20}=2,05\]
Ответ:
2,05
Найдите модуль разности корней уравнения \[x^2+2014x-2015=0\]
Нужно найти \(|x_1-x_2|\), если \(x_1, x_2\) – корни данного уравнения. По теореме Виета \(x_1x_2=-2015, x_1+x_2=-2014\), следовательно, \(x_1=-2015, x_2=1\). Тогда \[|x_1-x_2|=|-2015-1|=2016\]
Ответ:
2016
Решите уравнение \[\sin x+\sin 2x+\cos x=1\]
Пусть \(\sin x+\cos x=t\). Тогда \(t^2=(\sin x+\cos x)^2=\sin^2x+2\sin x\cos x+\cos^2x=1+\sin 2x\), следовательно, \(\sin 2x=t^2-1\). Тогда: \[t+t^2-1-1=0\quad\Rightarrow\quad \left[\begin{gathered}\begin{aligned} &t=-2\\ &t=1 \end{aligned}\end{gathered}\right.\] Так как \(\sin x+\cos x=\sqrt{2}\cdot \left(\frac{\sqrt2}2\sin x+\frac{\sqrt2}2\cos x\right)=\sqrt2\cdot \sin \left(x+\frac{\pi}4\right)\), то \[\left[\begin{gathered}\begin{aligned} &\sqrt2\cdot \sin \left(x+\dfrac{\pi}4\right)=-2 \\[2ex] &\sqrt2\cdot \sin \left(x+\dfrac{\pi}4\right) =1 \end{aligned}\end{gathered}\right.\quad\Leftrightarrow\quad \left[\begin{gathered}\begin{aligned} &\sin \left(x+\dfrac{\pi}4\right)=-\sqrt2 \\[2ex] &\sin \left(x+\dfrac{\pi}4\right) =\dfrac{\sqrt2}2 \end{aligned}\end{gathered}\right.\] Первое уравнение не имеет решений, так как область значений синуса – отрезок \([-1;1]\), а второе: \[\left[\begin{gathered}\begin{aligned} &x+\dfrac{\pi}4=\dfrac{\pi}4+2\pi n \\[2ex] &x+\dfrac{\pi}4=\dfrac{3\pi}4+2\pi k \end{aligned}\end{gathered}\right.\quad\Leftrightarrow\quad \left[\begin{gathered}\begin{aligned} &x=2\pi n \\[2ex] &x=\dfrac{\pi}2+2\pi k \end{aligned}\end{gathered}\right. \quad n,k\in\mathbb{Z}\]
Ответ:
\(2\pi n, \ \dfrac{\pi}2+2\pi k, \ n,k\in\mathbb{Z}\)
Решите неравенство \[\dfrac{4^{x^2}-16^{4x-8}}{\sqrt{x^2+4x}+\sqrt{12+4x-x^2}}>0\]
Заметим, что, так как \(\sqrt{f(x)}\geqslant 0\), знаменатель левой части всегда \(\geqslant 0\), причем равен нулю он только тогда, когда оба подкоренных выражения равны нулю. В нашем случае первое подкоренное выражение равно нулю при \(x=-4;0\), а второе – при \(x=-2;6\). Следовательно, оба выражения не могут одновременно равняться нулю, значит, \(\sqrt{x^2+4x}+\sqrt{12+4x-x^2}>0\) при всех \(x\) из ОДЗ. Тогда неравенство равносильно \[\begin{cases} 4^{x^2}-4^{8x-16}>0\\[2ex] x^2+4x\geqslant 0\\ 12+4x-x^2\geqslant 0 \end{cases}\] По методу рационализации неравенство \(a^x-a^y>0\) равносильно \((a-1)(x-y)>0\), следовательно, \[\begin{cases} (4-1)(x^2-8x+16)>0\\ x^2+4x\geqslant 0\\ 12+4x-x^2\geqslant 0 \end{cases} \quad\Leftrightarrow\quad \begin{cases} (x-4)^2>0\\ x\in (-\infty;-4]\cup[0;+\infty)\\ x\in [-2;6] \end{cases}\quad\Leftrightarrow\quad x\in [0;4)\cup(4;6]\]
Ответ:
\(x\in [0;4)\cup(4;6]\)
На стороне \(AB\) треугольника \(ABC\) отмечена точка \(D\). Окружности, вписанные в треугольники \(ACD\) и \(BCD\), касаются \(CD\) в точках \(E\) и \(F\) соответственно, причем \(CE:CF=1:2\). Найдите отношение \(AD:DB\), если известно, что радиусы указанных окружностей совпадают.
Рассмотрим чертеж:
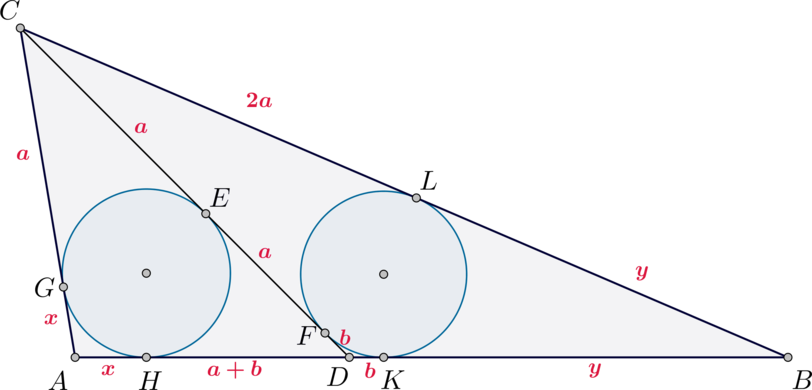
Точки \(G, H, E, F, K, L\) – точки касания окружностей со сторонами треугольников \(ACD\) и \(BCD\). Пусть \(CE=EF=a\), тогда \(CG=a, CL=2a\). Пусть \(AG=AH=x, FD=DK=b,
BK=BL=y\), тогда \(HD=a+b\).
Так как площади треугольников, имеющий одинаковую высоту, относятся как основания, к которым проведена эта высота, то \[\dfrac{S_{ACD}}{S_{BCD}}=\dfrac{AD}{BD}\] Если \(r\) – длина радиуса каждой окружности, то \(S_{ACD}=p_{ACD}\cdot r, \ S_{BCD}=p_{BCD}\cdot r\), где \(p\) – полупериметр треугольника. Следовательно, \[\dfrac{AD}{BD}=\dfrac{p_{ACD}}{p_{BCD}}\] Подставляя обозначения для сторон треугольников \(ACD\) и \(BCD\) через буквы \(a, b, x, y\), получим: \[\dfrac{2a+b+x}{2a+b+y}=\dfrac{x+a+b}{b+y}\quad\Rightarrow\quad
x+a=\dfrac{y-b}2\] Следовательно, \[\dfrac{AD}{BD}=\dfrac{b+\frac{y-b}2}{b+y}=\dfrac12\]
Ответ:
0,5
Ираида вышла из дому в 9:00 и направилась в магазин купить водички. Через некоторое время вслед за ней из дому выехал на велосипеде Ираклий в надежде нагнать ее и попросить купить еще и кефиру. Когда он догнал ее, они взглянули друг другу в глаза и поняли, что оба забыли дома деньги. Ираида молча пошла дальше в сторону магазина, а Ираклий поехал обратно за деньгами. Взяв дома деньги, Ираклий, не теряя ни секунды, поехал в сторону магазина и прибыл к нему одновременно с Ираидой в 9:15. Во сколько Ираклий впервые выехал из дому, если он за эти 15 минут преодолел в два раза большее расстояние, чем она? Скорости Ираклия и Ираиды считать постоянными.
Пусть встреча Ираклия и Ираиды произошла на расстоянии \(x\) (м) от дома (флажок).

Тогда за 15 минут Ираида прошла расстояние \(x+y\), а Ираклий проехал \(x+x+x+y\). Так как он проехал в два раза больше, то \[2(x+y)=3x+y\quad\Rightarrow\quad x=y\] Следовательно, они встретились на середине пути. Значит, если на весь путь Ираида затратила 15 минут, то на половину она затратила 7,5 минут. Следовательно, встретились они в 9 часов 7,5 минут.
Пусть \(v\) м/мин – скорость Ираиды, \(w\) м/мин – скорость Ираклия. Пусть \(t\) минут – время, которое он затратил на то, чтобы впервые догнать Ираиду (флажок).
Тогда \(t\cdot w=x\) и \(7,5\cdot w=3x\) (второе уравнение описывает движение Ираклия от места встречи до магазина через дом). Отсюда \[\dfrac {7,5}t=3\quad\Rightarrow\quad t=2,5\] Следовательно, до первой встречи Ираклий двигался 2,5 минуты, а раз встреча произошла в 9 часов 7,5 минут, то вышел из дому он в 9:05.
Ответ:
9:05
На ребрах \(AA'\) и \(BB'\) правильной треугольной призмы с основаниями \(ABC\) и \(A'B'C'\) отмечены точки \(D\) и \(E\), так что \(AD:DA'=B'E:EB=1:2\). Найдите угол между плоскостями \(ABC\) и \(DEC\), если известно, что данная призма является “каркасной”, то есть существует сфера, касающаяся всех ее ребер.
Так как существует сфера, касающаяся всех ребер призмы, то центр сферы точно лежит на прямой, равноудаленной от боковых ребер \(AA',
BB', CC'\). Следовательно, так как в основаниях лежат правильные треугольники, центр сферы лежит на прямой, соединяющей точки \(K\) и \(K'\) – точки пересечения медиан оснований (\(CN\) и \(C'N'\) – медианы).
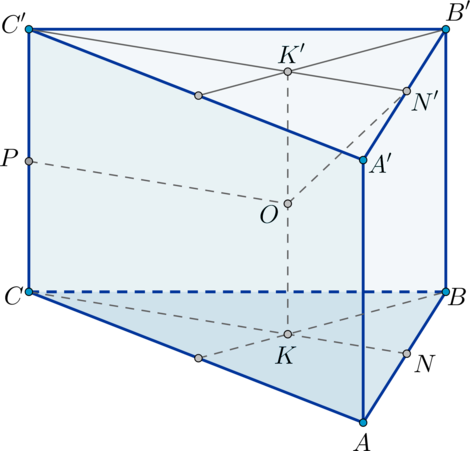
На рисунке для примера отмечен отрезок \(OP\) – расстояние от центра \(O\) сферы до ребра \(CC'\) (то есть радиус сферы).
Так как \(CK=C'K'\) и \(CK\parallel C'K'\), то \(CC'K'K\) – параллелограмм, откуда \(KK'\parallel CC'\). Следовательно, так как \(CC'\perp (A'B'C')\), то \(KK'\perp(A'B'C')\). Значит, \(KK'\perp
C'K'\).
Заметим, что тогда \(OP=C'K'\) (\(OP\perp CC', C'K'\perp CC'\), \(PC'\parallel OK'\), следовательно, \(PC'K'O\) – прямоугольник).
Так как \(KK'\perp (A'B'C')\), \(K'N'\perp A'B'\) как часть медианы в правильном треугольнике (а значит и высоты), то по теореме о трех перпендикулярах \(ON'\perp A'B'\). Следовательно, \(ON'\) – расстояние от центра сферы до ребра \(A'B'\).
Так как данная сфера касается всех ребер (то есть расстояние от центра сферы до всех ребер равно ее радиусу), то \[C'K'=OP=ON'\quad (*)\] Заметим, что также \(ON=ON'\) (радиусы сферы, проведенные к касательным ребрам), откуда следует, что \(\triangle
OKN=\triangle OK'N'\), следовательно, \(O\) – середина \(KK'\).
Пусть \(a\) – сторона основания призмы, \(h\) – высота. Следовательно, \(C'K'=\dfrac{a\sqrt3}3\), \(K'N'=\dfrac{a\sqrt3}6\), \(OK'=\dfrac h2\). Тогда из \((*)\) следует, что \[\dfrac{h^2}4+\dfrac{a^2\cdot 3}{36}=ON'^2=C'K'^2=\dfrac{a^2}3
\quad\Rightarrow\quad a=h\] Таким образом, мы выяснили, что боковое ребро призмы равно стороне основания.
Найдем теперь угол между плоскостью \(CDE\) и плоскостью \(ABC\):
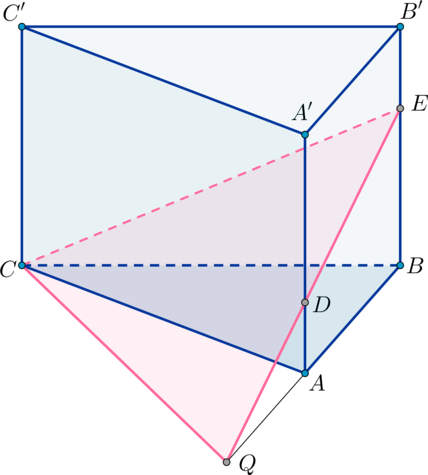
Продлим \(DE\) до пересечения с \(AB\) и получим точку \(Q\). Тогда \(CQ\) – прямая пересечения плоскостей \(CDE\) и \(ABC\). Так как \(AD:BE=1:2\) (из условия), то \(QA:QB=1:2\), откуда \(QA=AB\). То есть \(QA=AB=CA\). Следовательно, \(CA\) – медиана в \(\triangle QCB\), равная половине стороны, к которой она проведена. Значит, \(\triangle QCB\) прямоугольный с \(\angle QCB=90^\circ\). То есть \(BC\perp CQ\). Но тогда по теореме о трех перпендикулярах наклонная \(EC\perp CQ\). Следовательно, \(\angle ECB\) – линейный угол двугранного угла между плоскостями \(CDE\) и \(ABC\).
Так как \(BE=\frac23BB'=\frac23BC\), то \[\mathrm{tg}\,\angle ECB=\dfrac23\quad\Rightarrow\quad \angle ECB=
\mathrm{arctg} \dfrac23\]
Ответ:
\(\mathrm{arctg}\dfrac23\)
Решите систему уравнений \[\begin{cases} \log_{\sin x}\cos y=\log_{\cos x}\sin y\\[2ex] x^2+y^2=\dfrac{5\pi^2}{36} \end{cases}\]
1. Выпишем ОДЗ первого уравнения: \[\begin{cases}
\sin x>0\\
\sin x\ne 1\\
\cos y>0\\
\cos x>0\\
\cos x\ne 1\\
\sin y>0 \end{cases}\] Следовательно, \(x, y\) принадлежат первой четверти, то есть \(x\in \left(2\pi n; \dfrac{\pi}2+2\pi n\right)\) и \(y\in \left(2\pi n; \dfrac{\pi}2+2\pi n\right)\), \(n\in\mathbb{Z}\).
Рассмотрим первое уравнение. Так как на ОДЗ \(\log_ab=\log_{a^2}b^2\), то первое уравнение можно переписать в виде \[\log_{\sin ^2x}\cos^2y=\log_{\cos ^2x}\sin^2y\] Обозначим \(\sin^2x=t\), \(\cos^2y=z\). Тогда \(t\in (0;1)\) и \(z\in
(0;1)\) (учитывая ОДЗ).
Следовательно, уравнение примет вид: \[\log_tz=\log_{1-t}{(1-z)}\quad\Rightarrow\quad
\dfrac{\ln z}{\ln t}=\dfrac{\ln (1-z)}{\ln
(1-t)}\quad\Rightarrow\quad \dfrac{\ln (1-t)}{\ln t}=\dfrac{\ln
(1-z)}{\ln z}\] Полученное уравнение имеет вид \[f(t)=f(z)\] где \(f(t)=\dfrac{\ln (1-t)}{\ln t}\).
Исследуем данную функцию. Докажем, что она возрастает при всех \(t\in(0;1)\).
Для этого нужно доказать, что при увеличении \(t\) увеличивается и значение \(f(t)\).
Докажем, что для аргументов \(x\) и \(x-\varepsilon\) из интервала \((0;1)\), где \(\varepsilon\) – некоторое положительное число, выполнено: \(f(x)-f(x-\varepsilon)>0\).
Запишем: \[\log_x(1-x)-\log_{x-\varepsilon}(1-x+\varepsilon) \boxed{>}
\log_{x-\varepsilon}(1-x)-\log_{x-\varepsilon}(1-x+\varepsilon)=
\log_{x-\varepsilon}\dfrac{1-x}{1-x+\varepsilon}>0\] 1) Переход \(\boxed{>}\) верен, так как в \(\log_ab\) с \(a, b\in (0;1)\) при уменьшении \(a\) и фиксированном \(b\) уменьшается и значение \(\log_ab\).
2) Последний логарифм \(\log_{x-\varepsilon}\dfrac{1-x}{1-x+\varepsilon}\) положительный, так как и основание, и аргумент меньше единицы (это следует из свойств логарифмической функции).
Таким образом, мы доказали, что \(f(x)\) – возрастающая функция. Следовательно, равенство \(f(t)=f(z)\) возможно только в том случае, если \(t=z\).
2. Тогда первое уравнение системы принимает вид \[\sin^2x=\cos^2y\quad\Rightarrow\quad (\sin x-\cos y)(\sin x+\cos y)=0\] Так как \(\cos y=\sin \left(\dfrac{\pi}2-y\right)\), то полученное уравнение равносильно \[\left[\begin{gathered}\begin{aligned} &\sin x-\sin \left(\dfrac{\pi}2-y\right)=0\\[2ex] &\sin x+\sin \left(\dfrac{\pi}2-y\right)=0 \end{aligned}\end{gathered}\right.\quad\Rightarrow\quad \left[\begin{gathered}\begin{aligned} &2\sin \dfrac{x-\frac{\pi}2+y}2\cdot \cos\dfrac{x+\frac{\pi}2-y}2 =0\\[2ex] &2\sin \dfrac{x+\frac{\pi}2-y}2\cdot \cos\dfrac{x-\frac{\pi}2+y}2=0 \end{aligned}\end{gathered}\right.\quad\Rightarrow\quad \left[\begin{gathered}\begin{aligned} &x-\dfrac{\pi}2+y=2\pi n\\[2ex] &x+\dfrac{\pi}2-y=2\pi n\\[2ex] &x+\dfrac{\pi}2-y=\pi+2\pi n\\[2ex] &x-\dfrac{\pi}2+y=\pi+2\pi n \end{aligned}\end{gathered}\right. \ n\in\mathbb{Z}\] Данную совокупность можно переписать в виде: \[\left[\begin{gathered}\begin{aligned} &x-\dfrac{\pi}2+y=\pi n \\[2ex] &x+\dfrac{\pi}2-y=\pi n \end{aligned}\end{gathered}\right. \quad\Rightarrow\quad \left[\begin{gathered}\begin{aligned} &x=-y+\dfrac{\pi}2+\pi n\\[2ex] &x=y-\dfrac{\pi}2+\pi n \end{aligned}\end{gathered}\right. \quad n\in\mathbb{Z}\] Теперь осталось подставить полученные значения для \(x\) во второе уравнение изначальной системы и найти \(x\) и \(y\).
3. Рассмотрим первую серию \(x=-y+\dfrac{\pi}2+\pi n\), \(n\in\mathbb{Z}\).
Подставим во второе уравнение и получим \[2y^2-\pi(1+2n)y+\pi^2\cdot \left(n^2+n+\dfrac19\right)=0\] Дискриминант уравнения \(D=\pi^2\left(-4n^2-4n+\frac19\right)\). Он должен быть неотрицательным, следовательно, \[4n^2+4n-\dfrac19\leqslant 0\quad\Rightarrow\quad
n\in \left[-\dfrac12-\dfrac{\sqrt{10}}6;
-\dfrac12+\dfrac{\sqrt{10}}6\right]\quad\Rightarrow\quad n=-1;0\] (так как \(n\) – целое)
Тогда при \(n=0\) дискриминант равен \(D(0)=\dfrac{\pi^2}9\), следовательно, \[y=\dfrac{\pi \pm \dfrac{\pi}3}4\quad\Rightarrow\quad
y_1=\dfrac{\pi}3 \ \ {\small{\text{или}}} \ \ y_2=\dfrac{\pi}6\] Тогда \(x_1=\dfrac{\pi}6\) и \(x_2=\dfrac{\pi}3\). Данные пары \((x_1;y_1)\) и \((x_2;y_2)\) подходят по ОДЗ.
При \(n=-1\) дискриминант равен \(D(-1)=\dfrac{\pi^2}9\), следовательно, \(y_1=-\dfrac{\pi}3\) и \(y_2=-\dfrac{\pi}6\). Данные значения \(y\) не подходят по ОДЗ.
4. Рассмотрим вторую серию \(x=y-\dfrac{\pi}2+\pi n\), \(n\in\mathbb{Z}\).
Аналогично предыдущим рассуждениям, получаем, что при \(n=1\): \(y_1=-\dfrac{\pi}6\) и \(y_2=-\dfrac{\pi}3\). Данные значения не подходят по ОДЗ.
При \(n=0\): \(y_1=\dfrac{\pi}3\) и \(y_2=\dfrac{\pi}6\). Тогда при \(y_1\) получаем \(x_1=-\dfrac{\pi}6\), при \(y_2\) получаем \(x_2=-\dfrac{\pi}3\). Такие значения \(x\) также не подходят по ОДЗ.
5. Таким образом, окончательный ответ в задаче \[\left(\dfrac{\pi}6; \dfrac{\pi}3\right), \quad \left(\dfrac{\pi}3; \dfrac{\pi}6\right)\]
Ответ:
\(\left(\dfrac{\pi}6; \dfrac{\pi}3\right)\), \(\left(\dfrac{\pi}3; \dfrac{\pi}6\right)\)