\(\blacktriangleright\) Рациональное неравенство – это неравенство, которое можно свести к виду \[\large{\dfrac{P(x)}{Q(x)}\geqslant 0}
\quad (*)\] где \(P(x),\ Q(x)\) – многочлены.
(на месте знака \(\geqslant\) может стоять любой из знаков \(\leqslant, \
>,\
<\))
Способы решения данного неравенства:
1 способ: Классический. Т.к. дробь положительна (отрицательна) тогда и только тогда, когда числитель и знаменатель дроби одного знака (разных знаков), то неравенство \((*)\) равносильно совокупности:
\[{\large{\left[\begin{gathered}
\begin{aligned}
&\begin{cases} P(x)\geqslant 0\\ Q(x)>0 \end{cases}\\
&\begin{cases} P(x)\leqslant 0\\ Q(x)<0 \end{cases}
\end{aligned}
\end{gathered}
\right.}}\]
2 способ: Удобный. Метод интервалов (будем рассматривать этот метод на примере):
1 ШАГ. Разложим на множители числитель и знаменатель дроби.
Пусть после разложения неравенство примет вид \[\dfrac{x^2(x-1)^3(x+1)(2x^2+3x+5)(2x-x^2-3)}{(x+1)^3(3-x)(2-3x)^2} \geqslant0\] Помним, что если квадратное уравнение:
\(\sim\) имеет два корня \(x_1\) и \(x_2\) (дискриминант \(D>0\)), то \(ax^2+bx+c=a(x-x_1)(x-x_2)\).
\(\sim\) имеет один корень \(x_1\) (\(D=0\)), то \(ax^2+bx+c=a(x-x_1)^2\).
\(\sim\) не имеет корней (\(D<0\)), то квадратный трехчлен \(ax^2+bc+c\) никогда не может быть равен нулю, соответственно, не разлагается на линейные множители.
2 ШАГ. Рассмотрим скобки, в которых находится квадратный трехчлен с \(D<0\).
Если при \(x^2\) находится положительный коэффициент, то эти скобки можно вычеркнуть (в нашем неравенстве это \((2x^2+3x+5)\)).
Если при \(x^2\) находится отрицательный коэффициент, то при вычеркивании такой скобки знак неравенства меняем на противоположный (в нашем неравенстве это \((2x-x^2-3)\)).
Заметим, что если таких скобок несколько, то вычеркиваем их последовательно по одной, каждый раз меняя знак неравенства на противоположный.
Таким образом, неравенство примет вид \[\dfrac{x^2(x-1)^3(x+1)}{(x+1)^3(3-x)(2-3x)^2}
\leqslant0\]
3 ШАГ. Рассмотрим линейные скобки.
Назовем скобку хорошей, если при \(x\) находится положительный коэффициент (такие скобки не трогаем), и плохой, если при \(x\) находится отрицательный коэффициент (в таких скобках меняем все знаки на противоположные, т.е. делаем их хорошими).
Если плохих скобок было четное количество, то знак неравенства не изменится, если нечетное – то знак неравенства изменится на противоположный.
В нашем неравенстве одна скобка \((3-x)\) и две скобки \((2-3x)\) (т.к. \((2-3x)^2=(2-3x)(2-3x)\)), т.е. всего три плохих скобки, следовательно, неравенство примет вид: \[\dfrac{x^2(x-1)^3(x+1)}{(x+1)^3(x-3)(3x-2)^2}
\geqslant0\quad (**)\]
4 ШАГ. Отметим нули каждой скобки на числовой прямой, причем нули знаменателя – выколотые, нули числителя – закрашенные (если знак неравенства нестрогий, как у нас) или выколотые (если знак неравенства строгий).
Если мы отметили \(n\) точек, то числовая прямая разобьется на \(n+1\) промежутков.
Расставим знак на каждом промежутке справа налево.
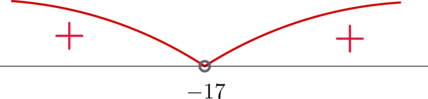
Т.к. все скобки – хорошие, то первый знак всегда будет \("+"\). Если какая-то точка входит в четное количество скобок, то при переходе через нее (справа налево!) знак меняться не будет (например, точка \(-1\) входит в четное количество скобок: одна в числителе и три в знаменателе);
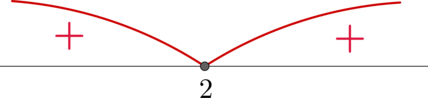
если точка входит в нечетное количество скобок, то знак будет меняться (например, точка \(3\)).

5 ШАГ. Запишем ответ. В нашем случае, т.к. знак преобразованного \((**)\) неравенства \(\geqslant 0\), то в ответ пойдут промежутки со знаком \("+"\) и закрашенные точки: \[x\in
(-\infty;-1)\cup \left(-1;\frac23\right)\cup
\left(\dfrac23;1\right]\cup(3;+\infty)\]