Подготовка к сдаче ЕГЭ по математике, как правило, начинается с повторения полной теории и базовых формул, в том числе и тех, с помощью которых можно найти площадь куба. И хотя эта тема достаточно подробно рассматривается преподавателями в рамках школьной программы, многим старшеклассникам требуется освежить в памяти основной материал.
Поняв, как найти объем куба и других параметров и отлично усвоив алгоритм решения таких задач, учащиеся смогут получить достаточно высокие баллы по итогам сдачи ЕГЭ.
Основные моменты
Чтобы вопрос, как вычислить объем куба, не ставил ученика в тупик, рекомендуем вспомнить основные свойства этой фигуры.
- Так как куб представляет собой прямоугольный параллелепипед, все шесть граней которого равны между собой, последние являются квадратами.
- Все двугранные углы многогранника прямые.
- Противоположные грани куба попарно параллельны.
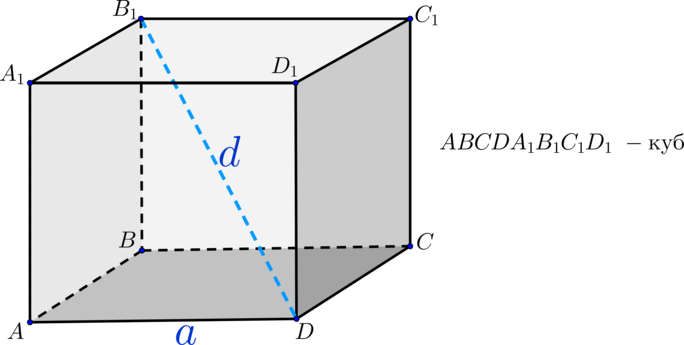
- Диагональ грани многогранника в √3 раза больше длины ребра.
- Если все линейные размеры сторон куба увеличиваются в k раз, то площадь его поверхности увеличивается в k2 раз.
Готовьтесь к единому госэкзамену качественно и эффективно вместе с образовательным проектом «Школково»
Занимаясь накануне прохождения аттестационного испытания, многие учащиеся сталкиваются с проблемой поиска базовой информации. Далеко не всегда школьный учебник оказывается под рукой. А на поиск подходящих формул для решения задач по теме «Куб» зачастую уходит большое количество времени.
Регулярные занятия на образовательном сайте «Школково» помогут учащимся избежать типовых ошибок при прохождении аттестационного испытания. Мы предлагаем выстроить процесс подготовки к экзамену по-новому, переходя от простого к сложному. Это позволит учащимся определить непонятные для себя темы и ликвидировать пробелы в знаниях.
Весь базовый материал представлен в разделе «Теоретическая справка». Основные понятия и формулы собраны и изложены нашими специалистами в максимально доступной форме.
Для того чтобы лучше усвоить материал, предлагаем также потренироваться в выполнении задач по темам «Куб», ”Прямоугольный параллелепипед”. Большая подборка упражнений различной степени сложности представлена в разделе «Каталог». Все задания содержат подробный алгоритм нахождения правильного ответа. База упражнений на сайте постоянно дополняется и обновляется.
В случае необходимости любое из представленных заданий можно сохранить в «Избранное». Это позволит в дальнейшем быстро его найти и обсудить алгоритм нахождения правильного ответа с преподавателем в школе или репетитором.