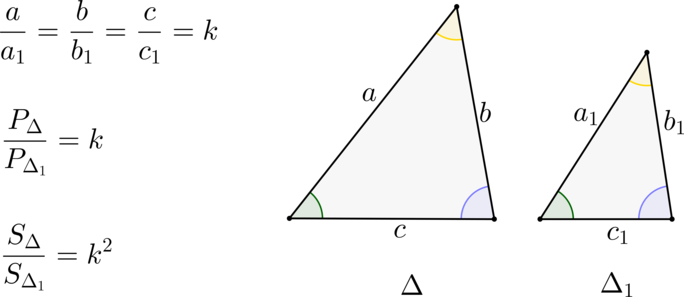\(\blacktriangleright\) Треугольники подобны, если их углы равны, а сходственные стороны (лежащие напротив равных углов) относятся друг к другу с одним и тем же коэффициентом \(k\) (пропорциональны).

\(\blacktriangleright\) Признаки подобия:

1. Два угла одного треугольника равны двум углам другого треугольника.

2. Три стороны одного треугольника пропорциональны трем сторонам другого треугольника.

3. Две стороны одного треугольника пропорциональны двум сторонам другого, а углы между этими сторонами равны.

\(\blacktriangleright\) Площади подобных треугольников относятся как \(k^2\), а периметры – как \(k\).

\(\blacktriangleright\) Средняя линия треугольника – отрезок, соединяющий середины двух сторон. Она равна половине третьей стороны.

Задание 1 #3935

Уровень задания: Равен ЕГЭ

Точка \(E\) лежит на стороне \(AC\) треугольника \(ABC\), причём \(\dfrac{EC}{AE} = 2\). Точка \(D\) лежит на \(BC\), причём \(ED\parallel AB\). Найдите \(AB\), если \(ED = \dfrac{4}{3}\).

Показать решение

Так как \(ED\parallel AB\), то \(\angle CED = \angle CAB\), \(\angle CDE = \angle CBA\) (как соответственные при параллельных прямых и секущей), тогда треугольники \(CED\) и \(CAB\) подобны.

Так как \(EC = 2\cdot AE\), то \(AC = 3\cdot AE\), следовательно, \[\dfrac{AC}{EC} = \dfrac{3\cdot AE}{2\cdot AE} = \dfrac{3}{2}.\]

Так как стороны \(EC\) и \(AC\) лежат против равных углов (в треугольниках \(CED\) и \(CAB\) соответственно), то \[\dfrac{AB}{ED} = \dfrac{AC}{EC} = \dfrac{3}{2},\] откуда \[AB = \dfrac{3}{2}\cdot ED = \dfrac{3}{2}\cdot\dfrac{4}{3} = 2.\]

Ответ: 2

Задание 2 #3937

Уровень задания: Равен ЕГЭ

Точка \(E\) лежит на стороне \(AC\) треугольника \(ABC\), причём \(\dfrac{EC}{AE} = 3\). Точка \(D\) лежит на \(BC\), причём \(\dfrac{CD}{CB} = 0,75\). Найдите \(\angle CED - \angle CAB\). Ответ дайте в градусах.

Показать решение

Рассмотрим треугольники \(CAB\) и \(CED\):
\(\angle C\) – общий,
\[\dfrac{CA}{CE} = \dfrac{AE + CE}{CE} = \dfrac{AE}{CE} + 1 = \dfrac{1}{3} + 1 = \dfrac{4}{3} = \dfrac{CB}{CD},\] тогда треугольники \(CAB\) и \(CED\) подобны по пропорциональности двух сторон и равенству углов между ними.

В подобных треугольниках против пропорциональных сторон лежат равные углы, тогда \(\angle CED = \angle CAB\), откуда \(\angle CED - \angle CAB = 0^{\circ}\).

Ответ: 0

Задание 3 #3943

Уровень задания: Равен ЕГЭ

\(F\) – точка пересечения \(AD\) и \(BE\) – медиан треугольника \(ABC\). Известно, что \(S_{ABF} = 1\). Найдите \(S_{DEF}\).

Показать решение

\(ED\) – средняя линия треугольника \(ABC\), тогда \(ED = 0,5\cdot AB\), \(ED\parallel AB\).

Так как \(ED\parallel AB\), то \(\angle DEF = \angle ABF\), \(\angle EDF = \angle FAB\) (как внутренние накрест лежащие при параллельных прямых и секущей), следовательно, треугольники \(DEF\) и \(ABF\) подобны (по двум углам). Так как \(ED = 0,5\cdot AB\), причём стороны \(ED\) и \(AB\) лежат (в треугольниках \(DEF\) и \(ABF\) соответственно) против равных углов, то \[\dfrac{S_{DEF}}{S_{ABF}} = \left(\dfrac{ED}{AB}\right)^2 = 0,5^2 = 0,25,\] откуда с учётом того, что \(S_{ABF} = 1\) находим \(S_{DEF} = 0,25\).

Ответ: 0,25

Задание 4 #3936

Уровень задания: Сложнее ЕГЭ

Отрезок \(BK\) соединяет вершину \(B\) треугольника \(ABC\) с точкой на противоположной стороне, причем \(\angle AKB = \angle B\). При этом известно, что \(BK = 10\), \(AB = 12\), \(AC = 18\). Найдите \(BC\).

Показать решение

Рассмотрим треугольники \(ABK\) и \(ACB\):
\(\angle AKB = \angle B\),
\(\angle A\) – общий, тогда треугольники \(ABK\) и \(ACB\) подобны по двум углам.

В подобных треугольниках против равных углов лежат пропорциональные стороны, тогда \[\dfrac{BK}{BC} = \dfrac{AB}{AC},\] откуда \(\dfrac{10}{BC} = \dfrac{12}{18}\), следовательно \(BC = 15\).

Ответ: 15

Задание 5 #3938

Уровень задания: Сложнее ЕГЭ

Отрезок \(BK\) соединяет вершину \(B\) треугольника \(ABC\) с точкой на противоположной стороне. При этом известно, что \(\angle AKB = 105^{\circ}\), \(AB = 12\), \(AC = 24\), \(AK = 6\). Найдите \(\angle ABC\). Ответ дайте в градусах.

Показать решение

Рассмотрим треугольники \(ABK\) и \(ACB\):
\(\angle A\) – общий,
\[\dfrac{AB}{AC} = \dfrac{AK}{AB},\] тогда треугольники \(ABK\) и \(ACB\) подобны по пропорциональности двух сторон и равенству углов между ними.

В подобных треугольниках против пропорциональных сторон лежат равные углы, тогда \(\angle ABC = \angle AKB = 105^{\circ}\).

Ответ: 105

Задание 6 #3939

Уровень задания: Сложнее ЕГЭ

На сторонах \(AB\), \(BC\) и \(AC\) треугольника \(ABC\) лежат точки \(D\), \(E\) и \(F\) соответственно. Известно, что \(\dfrac{DF}{BC} = 0,5\), \(AC = 2\cdot DE\), \(AB-EF=EF\) \(\angle DEF = 61^{\circ}\), \(\angle EFD = 55^{\circ}\). Найдите \(\angle C\). Ответ дайте в градусах.

Показать решение

Так как \(\angle DEF = 61^{\circ}\), \(\angle EFD = 55^{\circ}\), то \(\angle EDF = 180^{\circ} - 61^{\circ} - 55^{\circ} = 64^{\circ}\).

Рассмотрим треугольники \(ABC\) и \(EFD\): по условию
\[\dfrac{DF}{BC} = 0,5 = \dfrac{DE}{AC} = \dfrac{EF}{AB},\] тогда треугольники \(ABC\) и \(EFD\) подобны по пропорциональности трех сторон.

В подобных треугольниках против пропорциональных сторон лежат равные углы, тогда \(\angle C = \angle EDF = 64^{\circ}\).

Ответ: 64

Задание 7 #3940

Уровень задания: Сложнее ЕГЭ

Отрезок \(BK\) соединяет вершину \(B\) треугольника \(ABC\) с точкой на противоположной стороне. При этом известно, что \(AB = 12\), \(AC = 24\), \(AK = 6\), \(BK = 10\), \(BC = 20\). Найдите \(\angle AKB - \angle B\). Ответ дайте в градусах.

Показать решение

Рассмотрим треугольники \(ABK\) и \(ACB\):
\[\dfrac{AB}{AC} = \dfrac{AK}{AB} = \dfrac{BK}{BC},\] тогда треугольники \(ABK\) и \(ACB\) подобны по пропорциональности трех сторон.

В подобных треугольниках против пропорциональных сторон лежат равные углы, тогда \(\angle B = \angle AKB\), следовательно \(\angle AKB - \angle B = 0^{\circ}\).

Ответ: 0

предыдущая
подтема 1 2

Как показывает статистика, планиметрические задачи вызывают наибольшие сложности у учащихся старших классов. Именно поэтому школьникам будет полезно освежить в памяти основные принципы решения задач с подобными треугольниками при подготовке к ЕГЭ. Причем еще раз повторить эту тему стоит всем ученикам, независимо от того, профильный или базовый уровень планирует сдавать выпускник.

Вместе с образовательным порталом «Школково» вы сможете качественно подготовиться к аттестационному испытанию. Чтобы решение задач ЕГЭ по теме «Подобные треугольники» давалось легко, рекомендуем вспомнить основную теорию. Найти ее вы можете в соответствующем разделе нашего сайта. Здесь представлены основные признаки подобных треугольников (для решения заданий ЕГЭ знать их необходимо), формула отношения их площадей и другая базовая информация. Ее специалисты образовательного портала «Школково» подготовили и изложили в максимально доступной форме.

Отточить навык решения задач ЕГЭ на нахождение сторон и углов подобных треугольников, а также, например, задачи по теореме Пифагора учащиеся также смогут на нашем сайте. В разделе «Каталог» представлен широкий перечень упражнений различной сложности, который постоянно обновляется.

В каждом задании прописано решение и дан правильный ответ. Выполнять задачи с применением признаков подобия площадей подобных треугольников можно в режиме онлайн.

Любое из представленных упражнений при необходимости можно сохранить в разделе «Избранное». Таким образом, к нему возможно будет вернуться в дальнейшем, к примеру, для обсуждения с преподавателем.