Тренировочные варианты «Школково». Вариант Москва, июль 2017 года.

Сравним: \[\begin{aligned} \sqrt{\dfrac 79+7+\dfrac 97} \ &\lor \ 3\\[2ex] \dfrac 79+7+\dfrac 97 \ &\lor \ 9\\[2ex] \dfrac{7^2+7\cdot 7\cdot 9+9^2-9\cdot 7\cdot 9}{9\cdot 7} \ &\lor \ 0\\[2ex] \dfrac{7^2-2\cdot 7\cdot 9+9^2}{9\cdot 7} \ &\lor \ 0\\[2ex] \dfrac{(9-7)^2}{9\cdot 7} \ &\lor \ 0\\[4ex] \Rightarrow\quad \dfrac{(9-7)^2}{9\cdot 7}&>0 \end{aligned}\]

Таким образом, первое число больше второго.

Ответ:

первое больше

Так как \((a+b+c)^2=a^2+b^2+c^2+2ab+2bc+2ac\), то \[a^2+b^2+c^2=(a+b+c)^2-2(ab+bc+ac)=4^2-2\cdot 5=6\]

Ответ:

6

Так как \(\sin \alpha-\sin \beta=2\sin\dfrac{\alpha-\beta}2\cdot \cos\dfrac{\alpha+\beta}2\) и \(\cos \alpha-\cos\beta =-2\sin \dfrac{\alpha-\beta}2\sin \dfrac{\alpha+\beta}2\),   то уравнение можно переписать в виде: \[\begin{aligned} &2\sin \dfrac x2\cdot \cos\dfrac{15x}2-2\sin \dfrac x2\cdot \cos \dfrac x2=0 \quad\Rightarrow\quad 2\sin \dfrac x2\cdot \left( \cos\dfrac{15x}2-\cos \dfrac x2\right)=0\\ &\Rightarrow\quad -4\sin \dfrac x2\cdot \sin \dfrac{7x}2\cdot \sin 4x=0 \end{aligned}\] Полученное уравнение равносильно: \[\left[\begin{gathered}\begin{aligned} &\sin \dfrac x2=0\\[2ex] &\sin \dfrac{7x}2=0\\[2ex] &\sin 4x=0\end{aligned}\end{gathered}\right.\quad\Leftrightarrow\quad \left[\begin{gathered}\begin{aligned} &x=2\pi m\\[2ex] &x=\dfrac{2\pi}7n\\[2ex] &x=\dfrac{\pi}4k\end{aligned}\end{gathered}\right. \ m,n,k\in\mathbb{Z}\] Заметим, что первая серия корней полностью содержится в третьей серии корней, следовательно, ответ: \[x=\dfrac{2\pi}7n; \ \dfrac{\pi}4k; \ n,k\in\mathbb{Z}\]

Ответ:

\(\dfrac{\pi}4k; \dfrac{2\pi}7n; k,n\in\mathbb{Z}\)

ОДЗ неравенства: \(x>0\). Решим на ОДЗ.
Заметим, что \(x=1\) является решением неравенства, так как тогда неравенство принимает вид: \(0\leqslant 0\).
Пусть \(x\ne 1\). Тогда \(\log_4x\ne 0\), причем \(\log^2_4x>0\). Разделим обе части неравенства на \(\log^2_4x\): \[\begin{aligned} &\dfrac{\left(x\cdot \log_5x\right)^2}{\log^2_4x}+ 5\dfrac{\log^2_4x}{\log^2_4x}-\dfrac{x\cdot \log_5x\cdot 6\cdot \log_4x}{\log^2_4x}\leqslant 0\quad \Leftrightarrow\\[2ex] &\Leftrightarrow\quad \left(\dfrac{x\cdot \log_5x}{\log_4x}\right)^2-6\cdot \dfrac{x\cdot \log_5x}{\log_4x}+5\leqslant 0\end{aligned}\] Сделаем замену: \(\dfrac{x\cdot \log_5x}{\log_4x}=t\). Неравенство примет вид: \[t^2-6t+5\leqslant 0\quad\Rightarrow\quad 1\leqslant t\leqslant 5\] Заметим, что \[\dfrac{x\cdot \log_5x}{\log_4x}=x\cdot \dfrac{\log_x4}{\log_x5}=x\cdot \log_54=\dfrac x{\log_45}\] Следовательно: \[\begin{cases} \dfrac x{\log_45}\geqslant 1\\[2ex] \dfrac x{\log_45}\leqslant 5 \end{cases}\quad\Rightarrow\quad \begin{cases} x\geqslant \log_45\\ x\leqslant 5\log_45\end{cases}\] (так как \(\log_45>0\))

Полученные решения подходят по ОДЗ \(x>0\). Следовательно, окончательный ответ в неравенстве: \[x\in \{1\}\cup [\log_45; 5\log_45]\]

Ответ:

\(\{1\}\cup [\log_45; 5\log_45]\)

1) Рассмотрим чертеж:



Из условия следует, что \(A\) и \(C\) – точки касания. Следовательно, \(AB=CB\), то есть \(\triangle ABC\) равнобедренный.
Так как угол между касательной и хордой, проведенной из точки касания, равен половине дуги, заключенной между ними, то \(\angle DCA'=\angle CAD\). Аналогично \(\angle ACD=\angle DAC'\).
Таким образом, \(\triangle ADB'\sim\triangle CDA'\sim\triangle BDC'\) и \(\triangle CDB'\sim\triangle ADC'\).
Из этих подобий заключаем, что \[\dfrac{DB'}{DC'}=\dfrac{\sqrt7}7=\dfrac{AD}{BD},\] то есть можно обозначить \(AD=\sqrt7x, BD=7x\). Также: \[\dfrac{DB'}{DC'}=\dfrac{CD}{AD},\] откуда находим, что \(CD=x\).
Также: \[\dfrac{DA'}{DC'}=\dfrac{CD}{BD}\quad\Rightarrow\quad DA'=\dfrac{\sqrt7}7\]

2) Уже было сказано, что \(AB=BC\), то есть \(AC'+C'B=BA'+A'C\). Найдем данные отрезки по теореме Пифагора: \[\begin{aligned} &A'C=\sqrt{x^2-\dfrac17}\\[2ex] &BA'=\sqrt{49x^2-\dfrac17}\\[2ex] &C'B=\sqrt{49x^2-7}\\[2ex] &AC'=\sqrt{7x^2-7}\end{aligned}\] Таким образом, получаем уравнение: \[\sqrt{x^2-\dfrac17}+\sqrt{49x^2-\dfrac17}=\sqrt{7x^2-7}+\sqrt{49x^2-7} \quad\Rightarrow\quad \sqrt{49x^2-\dfrac17}-\sqrt{7x^2-7}=\sqrt{49x^2-7}-\sqrt{x^2-\dfrac17}\] Возведем в квадрат обе части уравнения и получим: \[\begin{aligned} &\sqrt{(7x^2-7)\left(49x^2-\frac17\right)}-3x^2=\sqrt{(49x^2-7)\left( x^2-\frac17\right)}\quad\Rightarrow\\[3ex] &\Rightarrow\quad \sqrt{(x^2-1)(343x^2-1)}-3x^2=\sqrt{(7x^2-1)(7x^2-1)}\quad\Rightarrow \quad \sqrt{(x^2-1)(343x^2-1)}-3x^2=7x^2-1 \end{aligned}\] так как \(7x^2-1=DA^2-DB'^2=AB'^2>0\).
Далее (возведем еще раз в квадрат и приведем подобные слагаемые): \[\sqrt{(x^2-1)(343x^2-1)}=10x^2-1\quad\Rightarrow\quad x^2(243x^2-324)=0\quad\Rightarrow\quad x=\dfrac2{\sqrt3}\] Следовательно, \[\sin\angle ACD=\dfrac1{\frac2{\sqrt3}}=\dfrac{\sqrt3}2\quad\Rightarrow\quad \angle ACD=60^\circ\]

Ответ:

\(60^\circ\)

Пусть \(x,y, z\) – скорость первого катера, второго (на котором плыл Григорий) и скорость течения реки соответственно (в км/ч).
Рассмотрим чертеж:



Пусть Григорий встретил Василия в точке D, пусть Григорий встретил друзей в точке K. Тогда \(AK=\frac34 AB, KB=\frac14AB\). Обозначим \(AB=s, CK=l\).
Так как путь \(AD\) плюс \(DK\) Григорий плыл столько же времени, за сколько проплыли его друзья путь \(AK\), то \[\dfrac{AD}{y+z}+\dfrac{DK}{y-z}=\dfrac{AK}{x+z} \quad\Rightarrow\quad \dfrac 6{y+z}+\dfrac{6-\frac34s}{y-z}=\dfrac{\frac34s}{x+z}\quad (1)\] Так как путь \(KC\) плюс \(CB\) Григорий плыл столько же времени, за сколько проплыли его друзья путь \(KB\), то \[\dfrac{KC}{y-z}+\dfrac{CB}{y+z}=\dfrac{KB}{x+z}\quad\Rightarrow\quad \dfrac l{y-z}+\dfrac{\frac14s+l}{y+z}=\dfrac{\frac14s}{x+z}\quad(2)\] Умножим 2-ое равенство на 3 и вычтем его из 1-ого равенства, получим: \[\dfrac{6-\frac 34s-3l}{y+z}+\dfrac{6-\frac34s-3l}{y-z}=0 \quad\Rightarrow\quad \left[\begin{gathered}\begin{aligned} &6-\frac34s-3l=0\\[1ex] &\dfrac 1{y+z}+\dfrac1{y-z}=0 \end{aligned}\end{gathered}\right. \quad\Rightarrow\quad \left[\begin{gathered}\begin{aligned} &s+4l=8\\[1ex] &y=0\end{aligned}\end{gathered}\right.\] Заметим, что \(y\ne 0\), так как это скорость катера, следовательно, верно: \(s+4l=8\). Так как \(BC=\frac14s+l=\frac14\left(s+4l\right)\), то \(BC=\frac14\cdot 8=2\) (км).

Ответ:

2 км

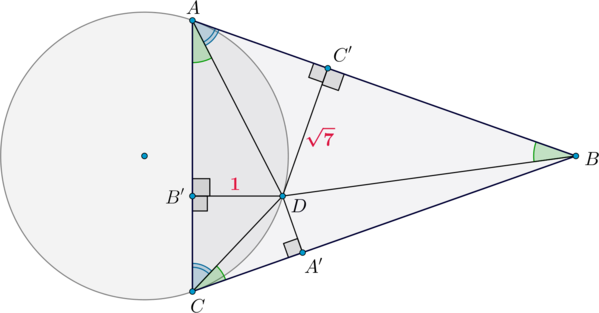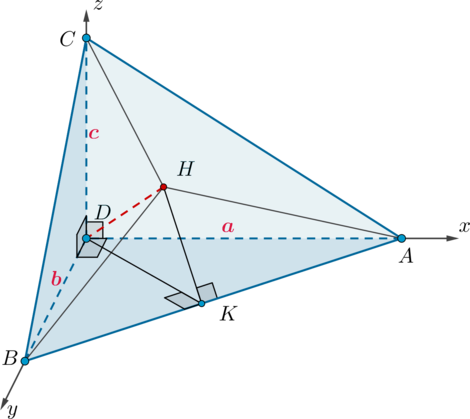
Введем прямоугольную систему координат так, как показано на рисунке. Пусть \(AD=a, BD=b, CD=c\). Тогда \(A(a;0;0)\), \(B(0;b;0)\), \(C(0;0;c)\), \(D(0;0;0)\).
Проведем \(HK\perp AB\). Так как \(DH\perp (ABC)\), то по теореме о трех перпендикулярах \(DK\perp AB\). Следовательно, \(S_{DAB}=0,5AB\cdot DK\), \(S_{HAB}=0,5 AB\cdot HK\). Так как из прямоугольного \(\triangle DHK\): \(HK=DK\cdot \cos\angle DKH\), то \[S_{HAB}=S_{DAB}\cdot \cos\angle DKH\quad (*)\] Заметим, что \(\angle DKH\) – угол между гранями \(ABC\) и \(DAB\).

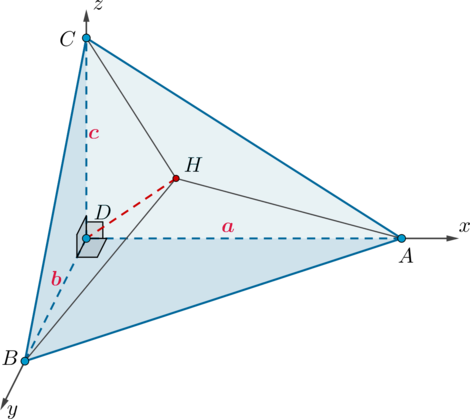
2)

Запишем подобные равенства для всех треугольников \(\triangle HAB, \triangle HAC, \triangle HBC\).
Уравнение плоскости \(DAB\): \(z=0\); плоскости \(DAC\): \(y=0\); плоскости \(DBC\): \(x=0\).
Уравнение плоскости \(ABC\): \(\frac xa+\frac yb+\frac zc=1\)
По формуле косинуса угла между плоскостями: \[\begin{aligned} &\cos \angle(ABC, DAB)=\dfrac{\frac 1c}{\sqrt{\frac 1{a^2}+\frac 1{b^2}+\frac 1{c^2}}}\\[2ex] &\cos \angle(ABC, DAC)=\dfrac{\frac 1b}{\sqrt{\frac 1{a^2}+\frac 1{b^2}+\frac 1{c^2}}}\\[2ex] &\cos \angle(ABC, DBC)=\dfrac{\frac 1a}{\sqrt{\frac 1{a^2}+\frac 1{b^2}+\frac 1{c^2}}}\end{aligned}\] Следовательно, так как \(S_{DAB}=0,5ab\), \(S_{DAC}=0,5ac\), \(S_{DBC}=0,5bc\), то \[\begin{cases} \dfrac 5{11}=\dfrac 12ab\cdot \dfrac{\frac 1c}{\sqrt{\frac 1{a^2}+\frac 1{b^2}+\frac 1{c^2}}}\\[2ex] \dfrac4{11}=\dfrac12ac\cdot \dfrac{\frac 1b}{\sqrt{\frac 1{a^2}+\frac 1{b^2}+\frac 1{c^2}}}\\[2ex] \dfrac2{11}=\dfrac12bc\cdot \dfrac{\frac 1a}{\sqrt{\frac 1{a^2}+\frac 1{b^2}+\frac 1{c^2}}} \end{cases}\quad (**)\] Разделим первое уравнение на второе, второе на третье и получим: \[\begin{cases} \dfrac 54=\dfrac{b^2}{c^2}\\[2ex] 2=\dfrac{a^2}{b^2} \end{cases}\quad\Rightarrow\quad \begin{cases} a^2=2b^2\\[2ex] c^2=\dfrac45b^2 \end{cases}\] Подставим полученные выражения для \(a\) и \(c\) через \(b\) в первое уравнение системы \((**)\), откуда найдем \(b^2\): \[b^2=\sqrt{\dfrac{10}{11}}\] Тогда \[a^2=2\sqrt{\dfrac{10}{11}}\quad {\small{\text{и}}}\quad c^2=\dfrac45 \sqrt{\dfrac{10}{11}}\] Так как объем пирамиды равен \[V=\dfrac13\cdot a\cdot \dfrac{bc}2=\dfrac16abc=\dfrac16 \cdot \sqrt{a^2b^2c^2}\] то: \[V=\dfrac2{33}\cdot \sqrt[4]{110}\]

Ответ:

\(\dfrac{2\sqrt[4]{110}}{33}\)

Обозначим для краткости \(x^2-y^2=t\). Возведем оба уравнения системы в квадрат и вычтем из первого уравнения второе: \[\left(\dfrac{x^2}{\cos^2t}+\dfrac{2xy\sin t}{\cos^2t}+ \dfrac{y^2}{\cos^2t}-y^2\right)-\left(\dfrac{y^2}{\cos^2t}+\dfrac{2xy\sin t}{\cos^2t}+ \dfrac{x^2}{\cos^2t}-x^2\right)=\dfrac{\pi}2-\dfrac{\pi}6\]

Полученное уравнение равносильно \(x^2-y^2=\dfrac{\pi}3\). Подставив это в уравнения изначальной системы, получим: \[\begin{cases} \dfrac x{\cos \frac{\pi}3}+y\cdot \mathrm{tg}\,\frac{\pi}3=\sqrt{\dfrac{\pi}2}\\[2ex] \dfrac y{\cos \frac{\pi}3}+x\cdot \mathrm{tg}\,\frac{\pi}3=-\sqrt{\dfrac{\pi}6} \end{cases} \quad\Rightarrow\quad \begin{cases} 2x+\sqrt3y=\sqrt{\dfrac{\pi}2}\\[2ex] 2y+\sqrt3x=-\sqrt{\dfrac{\pi}6}\end{cases} \quad\Rightarrow\quad \begin{cases} x=3\sqrt{\dfrac{\pi}2}\\[2ex] y=-5\sqrt{\dfrac{\pi}6}\end{cases}\]

Ответ:

\(x=3\sqrt{\frac{\pi}2}; \ y=-5\sqrt{\frac{\pi}6}\)