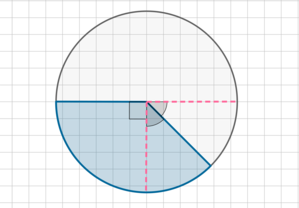
Задачи на нахождение площади круга — обязательная часть ЕГЭ по математике. Как правило, этой теме отводится сразу несколько заданий в аттестационном испытании. Понимать алгоритм нахождения длины окружности и площади круга должны все старшеклассники, независимо от уровня их подготовки.
Если подобные планиметрические задачи вызывают у вас затруднения, рекомендуем обратиться к образовательному порталу «Школково». С нами вы сможете восполнить пробелы в знаниях.
В соответствующем разделе сайта представлена большая подборка задач на нахождение длины окружности и площади круга, подобных тем, которые включены в ЕГЭ. Научившись их правильно выполнять, выпускник сможет успешно справиться с экзаменом.
Основные моменты
Задачи, в которых требуется применить формулы площади, могут быть прямыми и обратными. В первом случае известны параметры элементов фигуры. При этом искомой величиной является площадь. Во втором случае, наоборот, площадь известна, а найти необходимо какой-либо элемент фигуры. Алгоритм вычисления правильного ответа в подобных заданиях различается только порядком применения базовых формул. Именно поэтому, приступая к решению таких задач, необходимо повторить теоретический материал.
На образовательном портале «Школково» представлена вся базовая информация по теме «Нахождение длины окружности или дуги и площади круга», а также по другим темам, например, «Центральный угол окружности». Ее наши специалисты подготовили и изложили в максимально доступной форме.
Вспомнив основные формулы, учащиеся могут приступить к выполнению задач на нахождение площади круга, подобных тем, которые включены в ЕГЭ, в режиме онлайн. Для каждого упражнения на сайте представлено подробное решение и дан правильный ответ. При необходимости любое задание можно сохранить в разделе «Избранное», чтобы в дальнейшем вернуться к нему и обсудить с преподавателем.