Уровень Максим Олегович. Тренировочный вариант №6

Таблетка содержит \(16 \cdot 0,5 = 8\, мг\) активного вещества. Кириллу врач прописал принимать \(1 \cdot 40 = 40\, мг\) активного вещества в сутки. То есть ему надо принимать \(40 : 8 = 5\) таблеток в сутки.

Ответ: 5

По рисунку видно, что наибольшее количество осадков в день равно \(10\, мм\), а наименьшее – \(1\, мм\). Разница: \(10 - 1 = 9\, мм\).

Ответ: 9

Пусть \(h\) – длина высоты, опущенной из точки \(C\) на \(AB\), тогда \(S_{ABC} = 0,5\cdot AB\cdot h\).   \(S_{CEB} = 0,5\cdot EB\cdot h\), \(S_{CED} = 0,5\cdot DE\cdot h\), откуда \(\dfrac{6}{5} = \dfrac{S_{CEB}}{S_{CED}} = \dfrac{0,5\cdot EB\cdot h}{0,5\cdot DE\cdot h} = \dfrac{EB}{DE}\), но \(DE = AB - (AD + BE) = AB - \dfrac{2}{3}\cdot AB = \dfrac{1}{3}\cdot AB\), откуда \(EB = \dfrac{6}{5}\cdot \dfrac{1}{3}\cdot AB = \dfrac{2}{5}\cdot AB\), тогда \(AD = AB - (DE + EB) = AB - \dfrac{1}{3}\cdot AB - \dfrac{2}{5}\cdot AB = \dfrac{4}{15}\cdot AB\).
\(10 = S_{ACD} = 0,5\cdot AD\cdot h = 0,5\cdot \dfrac{4}{15}\cdot AB\cdot h = \dfrac{4}{15}\cdot S_{ABC}\), откуда \(S_{ABC} = 10\cdot\dfrac{15}{4} = 37,5\).

Ответ: 37,5

Так как вероятности выпадения любой упорядоченной пары чисел вида \((a; b)\) одинаковы (\(a\) и \(b\) – числа из множества \(1\), \(2\), \(3\), \(4\), \(5\), \(6\)), то искомая вероятность есть просто отношение суммарного количества пар \((a; b)\) таких, что \(a + b\) кратно \(3\), к общему количеству пар вида \((a; b)\). Сумма \(a + b\) кратна \(3\) в тех случаях, когда \(a + b = 3\) или \(a + b = 6\), или \(a + b = 9\), или \(a + b = 12\).

Под условие \(a + b = 3\) подходят \(2\) пары: \((1; 2)\) и \((2; 1)\),
под условие \(a + b = 6\) подходят \(5\) пар: \((1; 5)\), \((5; 1)\), \((2; 4)\), \((4; 2)\), \((3; 3)\),
под условие \(a + b = 9\) подходят \(4\) пары: \((3; 6)\), \((6; 3)\), \((4; 5)\), \((5; 4)\),
под условие \(a + b = 12\) подходит \(1\) пара: \((6; 6)\),
общее количество возможных пар вида \((a; b)\) равно \(36\).

Итого: искомая вероятность равна \[\dfrac{2 + 5 + 4 + 1}{36} = 0,(3).\] После округления до сотых получаем \(0,33\).

Ответ: 0,33

ОДЗ: \(x\) – произвольное. Решим на ОДЗ:

Можно угадать один из корней \(x = 1\). Знание этого корня позволяет вынести за скобку выражение \((x - 1)\) при помощи деления столбиком: \[\begin{array}{rr|l} x^3-21x^2+111x-91&&\negthickspace\underline{\qquad x-1 \qquad}\\ \underline{x^3\, -\ \ \ x^2} \phantom{00000000000}&&\negthickspace \ x^2 -20x + 91\\[-3pt] -20x^2 + 111x\,\phantom{0000}&&\\ \underline{-20x^2 +\ 20x\,}\phantom{0000}&&\\[-3pt] 91x - 91&&\\ \underline{91x - 91}&&\\[-3pt] 0&&\\ \end{array}\] тогда \[x^3 - 21x^2 + 111x - 91 = (x - 1)(x^2 - 20x + 91).\] Второй множитель также можно разложить в произведение линейных. Для этого находим корни уравнения \(x^2 - 20x + 91 = 0\). Его корни \(x_1 = 7, \ x_2 = 13\). Теперь разложение принимает окончательный вид:

\[x^3 - 21x^2 + 111x - 91 = (x^2 - 20x + 91)(x - 1) = (x - 7)(x - 13)(x - 1).\]

Произведение нескольких выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и все они не теряют смысл. Отсюда находим корни исходного уравнения: \(x_1 = 13, \ x_2 = 7, \ x_3 = 1\) – подходят по ОДЗ. Больший из них \(x = 13\).

Ответ: 13

Так как диагонали параллелограмма точкой пересечения делятся пополам, то \(BO = 0,5\cdot BD\).
Скалярное произведение вектора на себя равно квадрату его длины.
\(\overrightarrow{BD} = \overrightarrow{AD} - \overrightarrow{AB}\), тогда по свойству скалярного произведения имеем:

\[\begin{aligned} (\overrightarrow{BD}, \overrightarrow{BD}) &= (\overrightarrow{AD} - \overrightarrow{AB}, \overrightarrow{AD} - \overrightarrow{AB}) = (\overrightarrow{AD},\overrightarrow{AD} - \overrightarrow{AB}) + (- \overrightarrow{AB}, \overrightarrow{AD} - \overrightarrow{AB}) =\\ &= (\overrightarrow{AD}, \overrightarrow{AD}) - (\overrightarrow{AD}, \overrightarrow{AB}) - (\overrightarrow{AB}, \overrightarrow{AD}) + (\overrightarrow{AB}, \overrightarrow{AB}) = 5^2 - 2,5 - 2,5 + 4^2 = 36, \end{aligned}\]

откуда длина \(BD\) равна \(6\), тогда длина \(BO\) равна \(3\).

Ответ: 3

Для прямой, заданной уравнением \(y = kx + b\), коэффициент \(k\) есть значение тангенса угла между прямой \(y = kx + b\) и положительным направлением оси \(Ox\).

Таким образом, \(\mathrm{tg}\, \alpha = \sqrt{3}\). Так как градусная мера угла между двумя прямыми лежит в полуинтервале \([0; 180^{\circ})\), а \(\mathrm{tg}\, \alpha = \sqrt{3} > 0\), то \(0 < \alpha < \dfrac{\pi}{2}\), следовательно, \(\alpha = \mathrm{arctg}\, (\sqrt{3}) = \dfrac{\pi}{3}\). В итоге \(\alpha = 60^{\circ}\).

Ответ: 60

Рассмотрим прямоугольный треугольник \(AOB\): \(AO = 0,5h\), \(\angle ABO = 60^\circ\), \(OB = R\), тогда \(0,5h = R\cdot \mathrm{tg}\, 60^\circ = R\sqrt{3}\), откуда \(h = 2R\sqrt{3}\); \(AB = \dfrac{R}{\cos 60^\circ} = 2 R\).

\[\dfrac{75\sqrt{5}}{\sqrt{\pi}} = V_{\text{штрих}} = V_{\text{цил}} - V_{\text{кон}} = \pi R^2 h - \dfrac{1}{3}\pi R^2\cdot 0,5 h = \pi R^2\cdot\dfrac{5h}{6} = \pi R^3\dfrac{5\sqrt{3}}{3},\] тогда \(\dfrac{75\sqrt{5}}{\sqrt{\pi}} = \pi R^3\dfrac{5\sqrt{3}}{3}\), откуда \(R = \sqrt{\dfrac{15}{\pi}}\), тогда \[S_{\text{бок кон}} = \pi R\cdot AB = 2\pi R^2 = 30.\]

Ответ: 30

Так как \(\omega(\xi) = \sin \xi + \xi^{2017} + \xi^{2015} - \xi^{2013}\), то при любом числе \(\xi\) для числа \(-\xi\) имеем:

\(\omega(-\xi) = \sin (-\xi) + (-\xi)^{2017} + (-\xi)^{2015} - (-\xi)^{2013} = -\sin \xi - \xi^{2017} - \xi^{2015} +\xi^{2013} =\)
\(= -(\sin \xi + \xi^{2017} + \xi^{2015} - \xi^{2013}) = -\omega(\xi).\)

Тогда и для числа \(\xi = 2017^2\) выполнено \(\omega(-2017^2) = -\omega(2017^2)\), откуда \[\omega(2017^2) + \omega(-2017^2) + 15 = \omega(2017^2) -\omega(2017^2) + 15 = 15.\]

Ответ: 15

Моменты \(t\), в которые мячик находился на высоте не менее \(1\) метра, но не более \(2,2\) метров удовлетворяют двойному неравенству \[1 \leqslant 1 + 7t - 5t^2 \leqslant 2,2.\] Решим два неравенства по очереди.

Рассмотрим неравенство \(1 \leqslant 1 + 7t - 5t^2\). Оно равносильно неравенству \[5t^2 - 7t \leqslant 0,\] которое решим методом интервалов. Найдём корни уравнения \(5t^2 - 7t = 0\): \[t_1 = 0, \qquad\qquad t_2 = 1,4,\] тогда:



тогда решениями этого неравенства будут \(t\in[0; 1,4]\).

Рассмотрим теперь неравенство \(1 + 7t - 5t^2 \leqslant 2,2\). Оно равносильно неравенству \[5t^2 -7t + 1,2 \geqslant 0,\] которое решим методом интервалов. Найдём корни уравнения \(5t^2 -7t + 1,2 = 0\): \[t_1 = 0,2, \qquad\qquad t_2 = 1,2,\] тогда:



но с учётом того, что \(t \geqslant 0\) подходят только \(t\in[0; 0,2] \cup [1,2; +\infty)\).

В итоге мячик находился на высоте не менее \(1\) метра, но не более \(2,2\) метров в моменты \(t\in[0; 0,2] \cup [1,2; 1,4]\), то есть в течение \((0,2 - 0) + (1,4 - 1,2) = 0,4\) секунды.

Ответ: 0,4

В минуту каждая корова съедает \[\dfrac{1}{20} = 0,05\ \text{стога сена}.\] За \(5\) минут первая корова съела \(0,05 \cdot 5 = 0,25\) стога сена, после чего осталось \(1 - 0,25 = 0,75\) стога сена.

Поедая вместе, две коровы в минуту съедают \(2 \cdot 0,05 = 0,1\) стога сена, тогда с начала совместного поедания до конца прошло \(0,75 : 0,1 = 7,5\) минут.

Всего на стог сена коровам потребовалось \(5 + 7,5 = 12,5\) минут.

Ответ: 12,5

ОДЗ: \(e^x + 1 > 0\) – верно при любом \(x\). Решим на ОДЗ:

Заметим, что \[\dfrac{6}{e + 1}\] – просто число, тогда:

1) \[y' = \left(\dfrac{6}{e + 1}e^x - \ln((e^x + 1)^6)\right)' = \dfrac{6e^x}{e + 1} - 6\dfrac{e^x}{e^x + 1} = 6e^x\left(\dfrac{1}{e + 1} - \dfrac{1}{e^x + 1}\right).\]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна \(0\) или не существует): \[6e^x\left(\dfrac{1}{e + 1} - \dfrac{1}{e^x + 1}\right) = 0\qquad\Leftrightarrow\qquad \dfrac{1}{e + 1} - \dfrac{1}{e^x + 1} = 0\] (так как \(e^x > 0\) при любом \(x\)), что равносильно \(\dfrac{e^x - e}{(e+1)(e^x+1)} = 0\), откуда находим \(x = 1\). Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.

2) Найдём промежутки знакопостоянства \(y'\):



3) Эскиз графика \(y\):



Таким образом, \(x = 1\) – точка локального минимума функции \(y\).

Ответ: 1

ОДЗ: \(x\) – произвольное. Решим на ОДЗ:

а) Исходное уравнение можно переписать в виде

\[2^n\sin^{2n}x\cdot\cos^n x\cdot 2^m\sin^{2m}(2x)\cdot\cos^{2m} (2x) = 1,\]

что равносильно

\[(2\sin x\cdot\cos x)^n\cdot\sin^n x\cdot (2\sin (2x)\cdot\cos (2x))^m\sin^{m}(2x)\cdot\cos^{m} (2x) = 1,\]

что равносильно

\[\sin^n (2x)\cdot\sin^n x\cdot \sin^m (4x)\cdot\sin^{m}(2x)\cdot\cos^{m} (2x) = 1.\]

Так как в произведении в левой части стоят \(2n + 3m\) множителей, модули которых не больше \(1\), а правая часть равна \(1\), то модули каждого из множителей в левой части должны быть равны \(1\) (иначе модуль левой части будет меньше 1, а модуль правой равен 1 и равенство невозможно).

Заметим, однако, что \(|\sin x|\) и \(|\sin 2x|\) не могут одновременно быть равны 1, так как если \(|\sin x| = 1\), то из основного тригонометрического тождества следует, что \(\cos x = 0\), тогда \(|\sin 2x| = |2\sin x\cdot\cos x| = 0\). Отсюда следует, что у данного уравнения нет решений ни при каких \(n, m\in\mathbb{N}\).

Ответ:

а) \(\varnothing\)

б) \(\varnothing\)

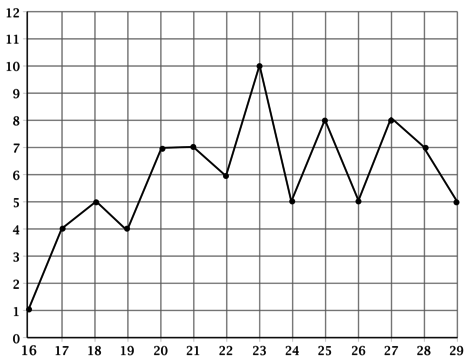
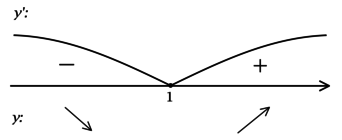
а)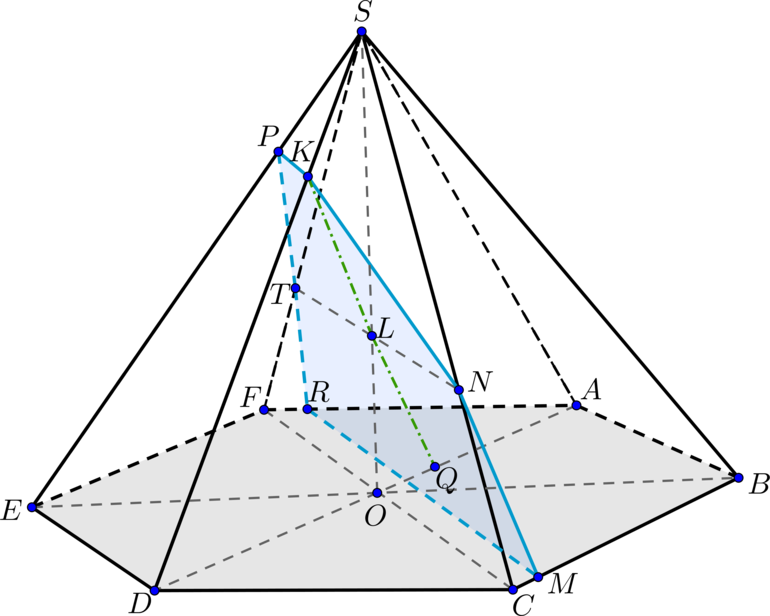

Две плоскости параллельны, если две пересекающиеся прямые из одной плоскости будут параллельны некоторых двум пересекающимся прямым из другой плоскости.Проведем через точку \(L\) прямые, параллельные \(AB\) и \(AS\).
Из свойства правильного шестиугольника следует, что \(FC\parallel AB\). Проведем в плоскости \(FSC\) через точку \(L\): \(TN\parallel FC\).

Тогда по теореме Фалеса \(\dfrac{SN}{NC}=\dfrac{ST}{TF}=\dfrac{SL}{LO}=\dfrac{3}{1}\)

В плоскости \(ASD\) проведем через точку \(L\): \(KQ\parallel SA\).

Из теоремы Фалеса следует, что \(\dfrac{AQ}{QO}=\dfrac{SL}{LO}=\dfrac{3}{1}\)

Пусть \(AQ=3x, QO=x\). Из свойств правильного шестиугольника следует, что \(DO=OA=4x\).

Тогда по теореме Фалеса \(\dfrac{DQ}{QA}=\dfrac{DK}{KS}=\dfrac{5x}{3x}=\dfrac{5}{3}\)

б) Достроим сечение пирамиды плоскостью \(\alpha\). Плоскость \(\alpha\) пересечет плоскость основания по прямой \(RM\parallel AB, Q\in RM\). Значит, \(\dfrac{BM}{MC}=\dfrac{AR}{RF}=\dfrac{3}{1}\)

Аналогично, плоскость \(\alpha\) пересекает грань \(SED\) по прямой \(PK\parallel ED\parallel AB\). Таким образом, \(MNKPTR\) – сечение.
Заметим, что сечение представляет собой две равнобокие трапеции \(MNTR\) и \(NKPT\).

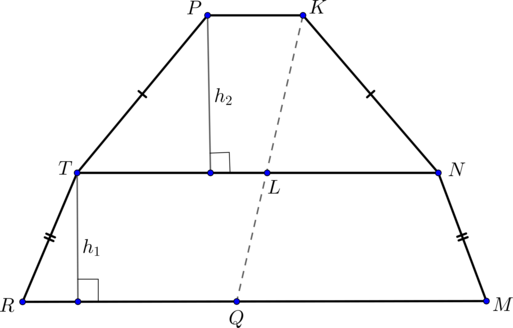
Найдем все их стороны.
Из подобия \(\bigtriangleup STN \sim \bigtriangleup SFC \Rightarrow TN=\dfrac{3}{4}FC=\dfrac{3}{2}a=6\)
Из подобия \(\bigtriangleup CNM \sim \bigtriangleup CSB \Rightarrow NM=\dfrac{1}{4}b=\dfrac{7}{4}\)

Достроим трапецию \(FABC\) до треугольника \(FWC\) – он правильный. \(\Rightarrow RM=\dfrac{7}{8}FC=\dfrac{7}{4}a=7\)
Из подобия \(\bigtriangleup SPK \sim \bigtriangleup SED \Rightarrow PK=\dfrac{3}{8}ED=\dfrac{3}{8}a=\dfrac{3}{2}\)

Найдем \(KN\) из грани \(SCD\):
По теореме косинусов \(cos\angle S=\dfrac{2b^2-a^2}{2b^2}\).

В \(\bigtriangleup KSN\): \(KN=\dfrac{3}{8}b, SN=\dfrac{3}{4}b \Rightarrow \) по теореме косинусов \(KN^2 =\dfrac{9}{64}\cdot (b^2 +2a^2) \Rightarrow KN=\dfrac{27}{8}\)

Обозначим высоту трапеции \(MNTR\) за \(h_1\). Тогда \(h_1 = \sqrt{\dfrac{49}{16}-\dfrac{1}{4}}=\dfrac{3}{4}\sqrt5\)

Высота трапеции \(NKPT\) \(h_1 =\sqrt{\dfrac{27^2}{64}-\dfrac{81}{16}}=\dfrac{9}{8}\sqrt5\)

Тогда площадь сечения \(S=\dfrac{1}{2}\cdot \left(\dfrac{3}{2}+6\right)\cdot \dfrac{9}{8}\sqrt5 + \dfrac{1}{2}\cdot (6+7)\cdot \dfrac{3}{4}\sqrt5 = \dfrac{291\sqrt5}{32}\)

Ответ:

б) \(\dfrac{291\sqrt5}{32}\)

ОДЗ: \[\begin{cases} 1 + Nx > 0\\ 1 + Nx\neq 1 \qquad\text{— при любых}\ N\in\mathbb{N}\\ 1 + x > 0 \end{cases}\]

Покажем, что \(x < 0\) не подходят по ОДЗ:
зафиксируем произвольное \(x < 0\), тогда \(-x > 0\). Существует \(n\in\mathbb{N}\), такое что \[n > \dfrac{1}{-x}\,.\] Положим \(N = n\), тогда \[N > \dfrac{1}{-x}\qquad\Rightarrow\qquad -xN > 1\qquad\Rightarrow\qquad 1 + Nx < 0,\] что не подходит по ОДЗ. Таким образом, \(x\geqslant 0\).

Также по ОДЗ не подходит \(x = 0\), а \(x > 0\) подходят по ОДЗ, следовательно,
ОДЗ: \[x > 0\,.\] На ОДЗ:
исходное неравенство равносильно неравенству

\[\begin{aligned} &\dfrac{1}{\log_{3}(1 + Nx)}\cdot\log_3(1 + x)^N\geqslant 1 \end{aligned}\]

Так как на ОДЗ \[1 + Nx > 1,\] то \(\log_{3}(1 + Nx) > 0\), следовательно,

\[\begin{aligned} &\dfrac{1}{\log_{3}(1 + Nx)}\cdot\log_3(1 + x)^N\geqslant 1\quad\Leftrightarrow\quad\log_3(1 + x)^N\geqslant \log_{3}(1 + Nx)\quad\Leftrightarrow\\ &\Leftrightarrow\quad (1 + x)^N\geqslant (1 + Nx). \end{aligned}\]

Зафиксируем произвольный \(x > 0\).
Докажем по индукции, что данное неравенство выполнено для всех \(N\in\mathbb{N}\):

1) \(N = 1\): \[1 + x \geqslant 1 + x\] – верно.

2) Рассмотрим произвольное \(m\in\mathbb{N}\), такое что \((1 + x)^m\geqslant 1 + mx\), тогда \[(1 + x)^{m + 1} = (1 + x)\cdot(1 + x)^m\geqslant (1 + x)\cdot(1 + mx) = 1 + mx + x + mx^2\geqslant 1 + x(m + 1),\] таким образом, мы доказали, что рассматриваемый \(x\) подходит. Так как мы фиксировали произвольный \(x > 0\), то все \(x > 0\) являются решениями исходной задачи.

Ответ:

\((0; +\infty)\)

а) Равенство длин \(AC\) и ломаной \(QAP\) равносильно равенству длин \(AQ\) и \(PC\).

На стороне \(AB\) отметим точку \(T\) так, что \(AT = AP\). Так как \(\triangle ABC\) – равносторонний, то \(AB = AC\), следовательно, \[\dfrac{AT}{AB} = \dfrac{AP}{AC}.\]

Рассмотрим треугольники \(ABC\) и \(ATP\): \[\dfrac{AT}{AB} = \dfrac{AP}{AC},\qquad\qquad \angle PAT \text{— общий},\] следовательно, они подобны по пропорциональности двух сторон и равенству углов между ними, откуда \[\dfrac{AT}{AB} = \dfrac{AP}{AC} = \dfrac{PT}{BC},\] следовательно, \(PT = AP = AT\).

Так как треугольник \(\angle APT\) – равносторонний, то \(\angle ATP = \angle TAP = 60^\circ\), откуда \(\angle BTP = \angle QAP\).

Кроме того, так как \(PQ = BP\), то \(\angle AQP = \angle ABP\). Из этого следует, что \[\angle APQ = 180^\circ - \angle AQP - \angle QAP = 180^\circ - \angle ABP - BTP = \angle BPT,\] следовательно, треугольники \(BTP\) и \(APQ\) равны по двум сторонам и углу между ними, откуда \[AQ = BT = AB - AT = AC - AP = PC.\]

б) \(AQ = PC = 4\). Так как \(\angle BAC = 60^\circ\), то \(\angle QAP = 120^\circ\), тогда \[S_{\triangle QAP} = 0,5\cdot 2\cdot 4\cdot\sin 120^\circ = 2\sqrt{3}.\]

Так как \(\triangle ABC\) – равносторонний с длиной стороны \(6\), то \[S_{\triangle ABC} = \dfrac{6^2\sqrt{3}}{4} = 9\sqrt{3}.\]

Таким образом, \[S_{BQPC} = S_{\triangle QAP} + S_{\triangle ABC} = 11\sqrt{3}.\]

Ответ:

б) \(11\sqrt{3}\).

Пусть \(A\) и \(x\) — суммы кредита и ежегодного платежа соответственно, а \(t=\frac{100+y}{100}\). Составим таблицу:

\[\begin{array}{|l|c|c|} \hline \text{Номер года}&\text{Долг после начисления }\%&\text{Долг после платежа}\\ \hline 1&tA&tA-x\\ \hline 2&t(tA-x)&t(tA-x)-x\\ \hline 3&t(t(tA-x)-x)&t(t(tA-x)-x)-x\\ \hline \end{array}\]

Таким образом,

\[t(t(tA-x)-x)-x=0 \quad \Leftrightarrow \quad \dfrac xA=\dfrac{t^3}{t^2+t+1}=\dfrac{27}{38}\]

Откуда получается уравнение \(38t^3-27t^2-27t-27=0\).

Известно, что \(y\) — целое кратное десяти число, то есть \(10; \ 20; \ 30; \dots\).

Тогда \(t=1,1; \ 1,2; \ 1,3; \dots\) или в рациональном виде \[t=\dfrac{11}{10}; \ \dfrac65; \ \dfrac{13}{10}; \ \dfrac75; \ \dfrac32; \ \dfrac85; \ \dfrac{17}{10}; \ \dfrac95; \ \dfrac{19}{10} \text{ и т.д.}\]

Если уравнение имеет рациональный корень, то числитель этого корня является делителем свободного члена, то есть \(-27\), а знаменатель — делителем старшего коэффициента, то есть \(38\). Таким образом, первый подходящий корень из нашего списка — это \(\frac{3}{2}\). Проверим:

\[38\cdot \left(\dfrac32\right)^3-27\left(\left(\dfrac32\right)^2+\dfrac32+1\right)=0 \quad \Leftrightarrow \quad 0=0\]

Таким образом, \(t=\dfrac32\) и \(y=50\%\).

Ответ:

\(50\%\)

Пусть \(x_0\) – общий корень данных уравнений. Заметим, что \(x_0\ne 0\) (т.к. \(0^3+a\cdot 0+1\ne 0\)). Тогда верна следующая система:

\[\begin{cases} x_0^3+ax_0+1=0\\ x_0^4+ax_0^2+1=0 \end{cases}\]

Умножим первое уравнение системы на \(x_0\) (имеем право, т.к. \(x_0\ne 0\)) и вычтем из полученного уравнения второе уравнение системы:

\[\begin{cases} x_0^4+ax_0^2+x_0-(x_0^4+ax_0^2+1)=0\\ x_0^4+ax_0^2+1=0 \end{cases} \quad \Rightarrow \quad \begin{cases} x_0=1\\ x_0^4+ax_0^2+1=0 \end{cases} \quad \Rightarrow \quad \begin{cases} x_0=1\\ a=-2 \end{cases}\]

Таким образом, данные уравнения общим корнем могут иметь только \(x_0=1\), и для того, чтобы \(x_0=1\) являлся их общим корнем, необходимо, чтобы \(a=-2\). Проверкой можно убедиться, что \(x_0=1\) и \(a=-2\) подходят в оба уравнения.

Ответ:

\(a\in \{-2\}\)

Убедимся, что любой общий делитель всякой пары натуральных чисел \((n; m)\) является также и общим делителем пары \((m; n - m)\): если уменьшаемое делится на число \(k\), то оно имеет вид \(n = ak\), если вычитаемое делится на число \(k\), то оно имеет вид \(m = bk\), тогда \[n - m = ak - bk = (a - b)k,\] то есть их разность также делится на число \(k\).

Аналогично доказывается, что любой общий делитель пары \((m; n - m)\) является общим делителем пары \((n; m)\), следовательно, \[\text{НОД}(n; m) =\ \text{НОД}(m; n - m).\]

Пусть \(n > m\). Можно свести НОД\((n; m)\) к наибольшему общему делителю другой пары чисел, в которой наибольшее из чисел окажется меньше, чем \(n\), а именно: НОД\((n; m) =\) НОД\((m; n - m)\).

Таким образом, можно получить последовательность равенств вида \(... =\) НОД\((k; 0)\) или вида \(... =\) НОД\((k; k)\), но НОД\((k; k) =\) НОД\((k; 0)\).

Такую последовательность действительно можно получить так как при \(n > m\) получается, что \(n > m\) и \(n > n - m\), то есть в равенстве НОД\((n; m) =\) НОД\((m; n - m)\) максимум из чисел под знаком НОД в правой части с каждым таким шагом уменьшается по крайней мере на 1, но числа \(n\) и \(m\) – конечны, следовательно, через конечное число преобразований можно получить цепочку равенств вида \(... =\) НОД\((k; 0)\).

\(\bullet\) Назовём выражение вида \(an + bm\), где \(a, b\in\mathbb{Z}\) линейной комбинацией над \(\mathbb{Z}\) чисел \(n\) и \(m\). Ясно, что сумма линейных комбинаций над \(\mathbb{Z}\) чисел \(n\) и \(m\) снова линейная комбинация над \(\mathbb{Z}\) чисел \(n\) и \(m\), разность линейных комбинаций над \(\mathbb{Z}\) чисел \(n\) и \(m\) снова линейная комбинация над \(\mathbb{Z}\) чисел \(n\) и \(m\).

Последнее полученное равенство можно продолжить: \[... =\ \text{НОД}(k; 0) = k.\] При этом число \(k\) получалось последовательным вычитанием из линейной комбинации над \(\mathbb{Z}\) чисел \(n\) и \(m\) линейных комбинаций над \(\mathbb{Z}\) чисел \(n\) и \(m\), то есть \(k\) есть линейная комбинация над \(\mathbb{Z}\) чисел \(n\) и \(m\), следовательно, существуют целые числа \(p\) и \(q\), такие что \(k = pn + qm\).

Ответ:

Доказательство