Тренировочные варианты «Школково». СтатГрад. Москва. 26 января 2018

Так как 399 человек – это \(19\%\), то \(1\%\) – это \(399:19=21\) человек. Следовательно, \(100\%\) – это \(21\cdot 100=2100\) человек.

Ответ: 2100

Вторая половина года – это все месяцы с июля по декабрь. Из диаграммы видно, что наименьшая температура была в декабре и равнялась \(2^\circ C\).

Ответ: 2

Из рисунка видно, что треугольник равнобедренный (\(BA=BC\)). Следовательно, биссектриса, опущенная из вершины \(B\), будет также являться медианой и высотой. Тогда биссектриса \(BH\) равна \(3\):

Ответ: 3

Найдем, сколько выступлений должно состояться в третий день. В первый день 12 выступлений, всего 75, следовательно, в последние три дня \(75-12=63\) выступления. Следовательно, в третий день \(63:3=21\) выступление.
Таким образом, вероятность того, что выступление исполнителя из России состоится в третий день, равна \[\dfrac{21}{75}=\dfrac7{25}=0,28\]

Ответ: 0,28

ОДЗ уравнения: \(x\in\mathbb{R}\).
Уравнение равносильно \(x-4=3^3\), следовательно, \(x=31\).

Ответ: 31

Так как медиана, опущенная из вершины прямого угла треугольника, равна половине гипотенузы, то \(\triangle BMC\) – равнобедренный, то есть \(BM=CM\). Следовательно, \(\angle BCM=\angle B=55^\circ\).
\(\angle BCH=90^\circ-\angle B=35^\circ\). Следовательно, \(\angle HCM=55^\circ-35^\circ=20^\circ\).

Ответ: 20

Значение производной в точке касания равно тангенсу угла наклона касательной к положительному направлению оси Ox. Рассмотрим \(\triangle ABC\):

Угол наклона касательной равен \(180^\circ-\angle ABC\). Из \(\triangle ABC\) видно, что \(\mathrm{tg}\,\angle ABC=10:8=1,25\). Так как \(\mathrm{tg}\,(180^\circ-\angle ABC)=-\mathrm{tg}\,\angle ABC\), то ответ: \(-1,25\).

Ответ: -1,25

Так как пирамида правильная, то в основании лежит правильный треугольник. Площадь правильного треугольника со стороной \(a\) равна \(S=\dfrac{\sqrt3}4a^2\). Следовательно, \(S=9\sqrt3\). Тогда объем равен \(V=\frac13Sh=\frac13\cdot 9\sqrt3\cdot 4\sqrt3=36\).

Ответ: 36

Заметим, что \(97^\circ\cdot 2=194^\circ\). Следовательно: \[\dfrac{-10\sin 97^\circ\cdot \cos 97^\circ}{\sin (2\cdot 97^\circ)}= \dfrac{-10\sin 97^\circ\cdot \cos 97^\circ}{2\sin 97^\circ\cdot \cos97^\circ}=-5\]

Ответ: -5

Подставим данные в формулу: \[2\cdot 10^5\cdot V^{\frac43}=1,25\cdot 10^8\quad\Leftrightarrow\quad \sqrt[3]{V^4}=10^3\cdot \dfrac{10}8\cdot \dfrac12\quad\Rightarrow\quad V=\left(10^4\cdot \dfrac1{2^4}\right)^{\frac34}=10^3\cdot \dfrac1{2^3}=\dfrac{1000}8=125\]

Ответ: 125

Пусть \(x\) км/ч – скорость автомобиля. Пусть \(y\) км – расстояние от города A до города C. Тогда время, которое затратил автомобиль на путь AC, равно \(\dfrac yx\) (ч). Время, которое затратил мотоцикл на этот же путь, равно \(\dfrac y{90}\) (ч).   Так как мотоцикл выехал на час позже, то он затратил на 1 час меньше времени, следовательно, \[\dfrac yx-1=\dfrac y{90}\] Это первое уравнение.
На весь путь от A до B автомобиль затратил \(\dfrac{403}x\) (ч). Мотоцикл затратил на путь из C в A столько же времени, сколько на путь из A в C (так как обратно он ехал с той же скоростью, что и в C). Следовательно, на путь от A до C и обратно мотоцикл затратил \(\dfrac {2y}{90}\). Заметим, что в сумме мотоцикл двигался также на 1 час меньше времени, чем автомобиль: \[\dfrac{403}x-1=\dfrac{2y}{90}\] Это второе уравнение. Составим систему: \[\begin{cases} \dfrac yx-1=\dfrac y{90}\\[2ex] \dfrac{403}x-1=\dfrac{2y}{90} \end{cases}\] Выразим \(x\) из первого уравнения: \(x=\dfrac{90y}{90+y}\) и подставим во второе уравнение, получим: \[2y^2-313y-403\cdot 90=0\] Дискриминант \(D=313^2+2\cdot 4\cdot 403\cdot 90=388\,129\). Извлечем корень из данного числа. Так как \(600^2=360\,000\), а \(700^2=490\,000\), то \(600<\sqrt{388\,129}<700\). Так как \(61^2=3721\), \(62^2=3844\), \(63^2=3969\), то \(620<\sqrt{388\,129}<630\). Подберем последнюю цифру: на конце дают \(9\) следующие цифры, возведенные в квадрат: \(3\) и \(7\) (\(3^2=9, 7^2=49\)). Проверим: \(623^2=388\,129\). Таким образом, \(\sqrt{D}=623\).
Найдем корни: \[y_{1,2}=\dfrac{313\pm623}{4}\quad\Rightarrow\quad \left[\begin{gathered}\begin{aligned} &y=234\\&y=-77,5\end{aligned}\end{gathered}\right.\] Так как \(y\) – расстояние, то есть величина неотрицательная, то подходит только корень \(y=234\).

Ответ: 234

1 способ.

Заметим, что \[x^2+18x+79=x^2+18x+81-2=(x+9)^2-2\] Следовательно, \(y=\sqrt{-(x+9)^2+2}\). Так как \((x+9)^2\geqslant 0\), то \(-(x+9)^2+2\leqslant 2\).
Заметим, что при \(x<-9\) функция \(y(x)\) является возрастающей, так как при увеличении \(x\) значение \(y(x)\) также растет. А при \(x>-9\) функция является убывающей. Следовательно, \(x=-9\) – точка максимума.

2 способ.

Найдем производную функции, чтобы схематично построить график этой функции.

\[y'=(\sqrt{-79-18x-x^2})'\cdot (-79-18x-x^2)'=\dfrac 1{2\sqrt{-79-18x-x^2}}\cdot (-2x-18)\] Найдем нули производной: \[y'=0\quad\Rightarrow\quad x=-9\] Заметим, что \(x=-9\) подходит по ОДЗ (\(-79-18x-x^2\geqslant 0\)). Найдем знаки производной справа и слева от точки \(x=-9\):

Таким образом, по определению точка \(x=-9\) является точкой максимума.

Ответ: -9

а) По формулам приведения \(\sin(\pi+x)=-\sin x, \ \sin\left(\dfrac{\pi}2+x\right)=\cos x\). Тогда уравнение примет вид \[-2\sin x\cos x=\sin x\quad\Leftrightarrow\quad \sin x(1+2\cos x)=0 \quad\Leftrightarrow\quad\left[\begin{gathered}\begin{aligned} &\sin x=0\\[1ex]&\cos x=-\dfrac12\end{aligned}\end{gathered}\right.\] Корнями уравнений будут являться \(x=\pi n\) и \(x=\pm\dfrac{2\pi}3+2\pi k\), \(n,k\in\mathbb{Z}\).  

б) Отберем корни.   \(2\pi\leqslant \pi n\leqslant \dfrac{7\pi}2\quad\Leftrightarrow\quad 2\leqslant n\leqslant 3,5\quad\Rightarrow\quad n=2;3\quad\Rightarrow\quad x=2\pi; 3\pi\)   \(2\pi\leqslant \dfrac{2\pi}3+2\pi k\leqslant \dfrac{7\pi}2\quad\Leftrightarrow\quad \dfrac23\leqslant k\leqslant \dfrac{17}{12}\quad\Rightarrow\quad k=1\quad\Rightarrow\quad x=\dfrac{8\pi}3\)   \(2\pi\leqslant -\frac{2\pi}3+2\pi k\leqslant \dfrac{7\pi}2\quad \Leftrightarrow\quad \dfrac43\leqslant k\leqslant \dfrac{25}{12}\quad\Rightarrow\quad k=2\quad\Rightarrow\quad x=\dfrac{10\pi}3\)

Ответ:

а) \(\pi n, \ \pm \dfrac{2\pi}3+2\pi k, \ n,k\in\mathbb{Z}\)

б) \(2\pi, \ \dfrac{8\pi}3, \ 3\pi, \ \dfrac{10\pi}3\)

а) По свойству правильной пирамиды \(PD=PB\). Так как \(PD\) перпендикулярно плоскости \(\alpha\) сечения, то оно перпендикулярно любой прямой из плоскости \(\alpha\). Следовательно, \(PD\perp BK\). Тогда \(BK\) – медиана и высота в \(\triangle BPD\), следовательно, этот треугольник равнобедренный и \(BP=BD\). Следовательно, \(\triangle BPD\) – равносторонний и \(\angle PDB=60^\circ\). Но это и есть угол между боковым ребром \(PD\) и плоскостью основания, чтд.

б) Проведем еще одну прямую, пересекающую \(BK\) и перпендикулярную \(PD\). Тогда плоскость, проходящая через эту прямую и прямую \(BK\), и будет плоскостью \(\alpha\).
Так как диагонали квадрата взаимно перпендикулярны, то \(AC\perp BD\). Тогда по теореме о трех перпендикулярах наклонная \(PD\) также будет перпендикулярна \(AC\).
Следовательно, если провести через точку пересечения \(PO\) и \(BK\) прямую \(MN\) параллельно \(AC\), то \(MN\perp PD\). Проведем:

Таким образом, \(BMKN\)– искомое сечение.
Заметим, что аналогично по теореме о трех перпендикулярах \(BK\perp MN\). Следовательно, \(S_{BMKN}=\frac12BK\cdot MN\cdot \sin\angle BQN\), а \(\sin\angle BQN=1\), следовательно, \[S_{BMKN}=\dfrac12BK\cdot MN\] Рассмотрим \(\triangle BKD\). \(BD=6\sqrt2\), \(KD=0,5PD=0,5BD=3\sqrt2\). Следовательно, по теореме Пифагора \[BK=3\sqrt6\] Так как \(PO\) и \(BK\) – медианы в \(\triangle BPD\), то \(PQ:QO=2:1\), следовательно, \(PQ:PO=2:3\).
Так как \(\triangle APC\sim MPN\), то \[MN:AC=PQ:PO\quad\Rightarrow\quad MN=\dfrac23\cdot 6\sqrt2=4\sqrt2\] Следовательно, \[S_{BMKN}=\dfrac12\cdot 3\sqrt6\cdot 4\sqrt2=12\sqrt3\]

Ответ:

б) \(12\sqrt3\)

Выпишем ОДЗ неравенства: \[\begin{cases} (x+4)^2>0\\ (x+4)^2\ne 1\\3x^2-x-1>0\end{cases}\quad\Leftrightarrow\quad x\in (-\infty;-5)\cup(-5;-4)\cup(-4;-3)\cup\left(-3;\dfrac{1-\sqrt{13}}6\right) \cup\left(\dfrac{1+\sqrt{13}}6;+\infty\right)\] Решим неравенство на ОДЗ. Воспользуемся методом рационализации: \[((x+4)^2-1)\cdot (3x^2-x-1-1)\leqslant 0\quad\Leftrightarrow\quad (x+3)(x+5)(x-1)(3x+2)\leqslant 0\] Решим данное неравенство методом интервалов:

Следовательно, \[x\in [-5;-3]\cup\left[-\dfrac23;1\right]\] Пересечем полученный ответ с ОДЗ и найдем итоговый ответ: \[x\in (-5;-4)\cup(-4;-3)\cup\left[-\dfrac23;\dfrac{1-\sqrt{13}}6\right) \cup\left(\dfrac{1+\sqrt{13}}6;1\right]\]

Ответ:

\((-5;-4)\cup(-4;-3)\cup\left[-\dfrac23;\dfrac{1-\sqrt{13}}6\right) \cup\left(\dfrac{1+\sqrt{13}}6;1\right]\)

а) Угол \(BOC\) – центральный, опирающийся на дугу \(BC\); угол \(BKC\) – вписанный и опирающийся на ту же дугу, следовательно, \(\angle BOC=2\angle BKC\), чтд.

б) Проведем \(KH\perp BC\). Так как угол между касательной и хордой, выходящей из точки касания, равен половине дуги, заключенной между ними, то \(\angle DKC=0,5\buildrel\smile\over{KC}=\angle KBC\). Аналогично \(\angle AKB=\angle KCB\):

Следовательно, \(\triangle AKB\sim \triangle KHC, \triangle KDC\sim \triangle KHB\) как прямоугольные по острому углу. Тогда: \[\begin{aligned} &\dfrac{KB}{KC}=\dfrac{KH}{CD}\\[2ex] &\dfrac{KC}{KB}=\dfrac{KH}{AB}\end{aligned}\] Отсюда \[1=\dfrac{KH^2}{CD\cdot AB}\quad\Rightarrow\quad KH=\sqrt{CD\cdot AB}=\sqrt{ 4\cdot 9}=6\]

Ответ:

б) 6

Пусть \(A\) – сумма кредита в рублях. Пусть \(x\) – платеж в рублях в случае, если кредит взят на три года, \(y\) – платеж в рублях в случае, если кредит взят на два года. Так как по условию платежи аннуитетные, то, если кредит взят на три года, то в конце третьего года долг будет равен \[1,1^3\cdot A-x(1,1^2+1,1+1)=0\] Если кредит взят на два года, то в конце второго года долг будет равен \[1,1^2\cdot A-y(1,1+1)=0\] Если вы не понимаете, почему так, можете ознакомиться с теорией по ссылке https://shkolkovo.net/theory/44   В первом случае клиент выплатит банку за все года \(3x\) рублей, во втором – \(2y\) рублей. Следовательно, нужно найти \(3x-2y\). Найдем:   \(3x-2y=\dfrac{3\cdot 1,1^3\cdot A}{1,1^2+1,1+1}-\dfrac{2\cdot 1,1^2\cdot A} {1,1+1}=\)   \(=1,1^2\cdot A\cdot \dfrac{3\cdot 1,1^2+3\cdot 1,1-2\cdot 1,1^2-2\cdot 1,1-2}{2,1\cdot 3,31}=1,1^2\cdot A\cdot \dfrac{0,31}{2,1\cdot 3,31}=\)   \(=\dfrac{11\cdot 11\cdot 6951\cdot 31}{21\cdot 331}=11\cdot 11\cdot 31=3\,751\).

Ответ: 3751

1) Рассмотрим первое уравнение системы как квадратное относительно \(x\): \[2x^2-(5y)x+2y^2=0\] Дискриминант равен \(D=9y^2\), следовательно, \[x_{1,2}=\dfrac{5y\pm 3y}4\quad\Rightarrow \quad x_1=2y, \quad x_2=\dfrac12y\] Тогда уравнение можно переписать в виде \[(x-2y)\cdot (2x-y)=0\] Следовательно, всю систему можно переписать в виде \[\begin{cases} \left[\begin{gathered}\begin{aligned} &y=2x\\[1ex] &y=0,5x\end{aligned}\end{gathered}\right.\\[1ex] (x-a)^2+(y-a)^2=5a^4\end{cases}\] Совокупность задает две прямые, второе уравнение системы задает окружность с центром в \((a;a)\) и радиусом \(R=\sqrt5a^2\). Чтобы исходное уравнение имело два решения, нужно, чтобы окружность пересекала график совокупности ровно в двух точках. Вот чертеж, когда, например, \(a=1\):

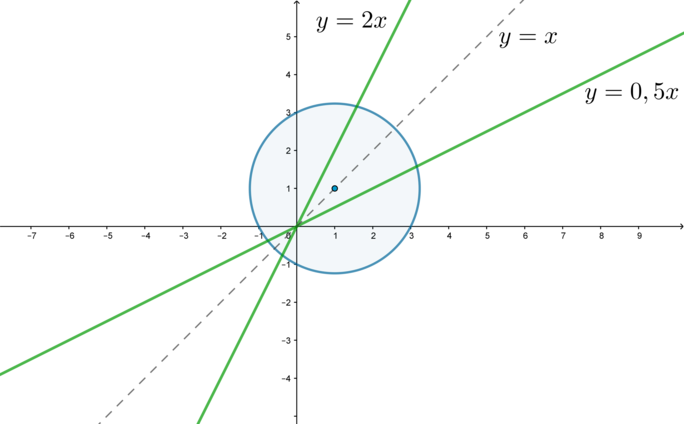
Заметим, что так как координаты центра окружности равны, то центр окружности “бегает” по прямой \(y=x\).

2) Так как у прямой \(y=kx\) тангенс угла наклона этой прямой к положительному направлению оси \(Ox\) равен \(k\), то тангенс угла наклона прямой \(y=0,5x\) равен \(0,5\) (назовем его \(\mathrm{tg}\,\alpha\)), прямой \(y=2x\) – равен \(2\) (назовем его \(\mathrm{tg}\,\beta\)). Заметим, что \(\mathrm{tg}\,\alpha\cdot \mathrm{tg}\,\beta=1\), следовательно, \(\mathrm{tg}\,\alpha=\mathrm{ctg}\,\beta=\mathrm{tg}\,(90^\circ-\beta)\). Следовательно, \(\alpha=90^\circ-\beta\), откуда \(\alpha+\beta=90^\circ\). Это значит, что угол между \(y=2x\) и положительным направлением \(Oy\) равен углу между \(y=0,5x\) и положительным направлением \(Ox\):

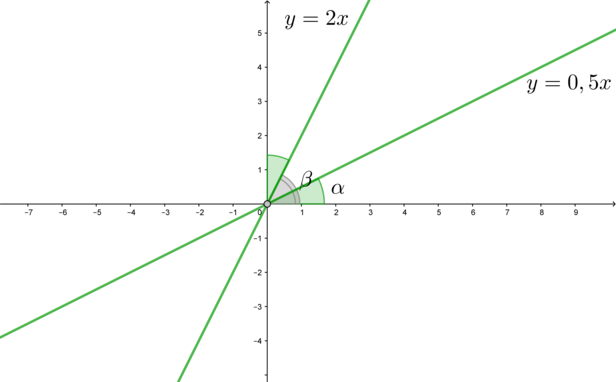
А так как прямая \(y=x\) является биссектрисой I координатного угла (то есть углы между ней и положительными направлениями \(Ox\) и \(Oy\) равны по \(45^\circ\)), то углы между \(y=x\) и прямыми \(y=2x\) и \(y=0,5x\) равны.
Все это нам нужно было для того, чтобы сказать, что прямые \(y=2x\) и \(y=0,5x\) симметричны друг другу относительно \(y=x\), следовательно, если окружность касается одной из них, то она обязательно касается и второй прямой.
Заметим, что если \(a=0\), то окружность вырождается в точку \((0;0)\) и имеет лишь одну точку пересечения с обеими прямыми. То есть этот случай нам не подходит.
Таким образом, для того, чтобы окружность имела 2 точки пересечения с прямыми, нужно, чтобы она касалась этих прямых:

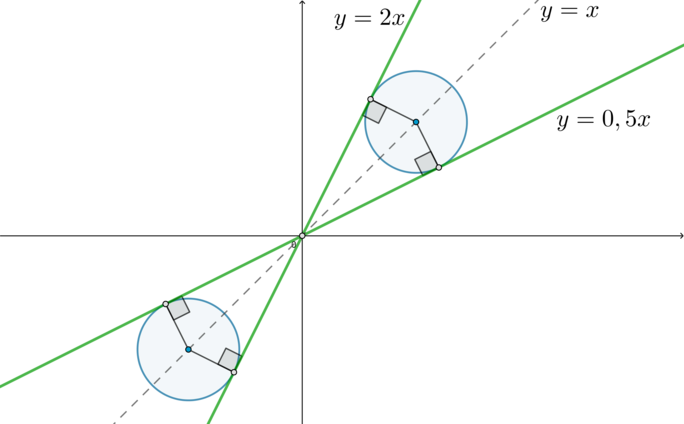
Видим, что случай, когда окружность располагается в третьей четверти, симметричен (относительно начала координат) случаю, когда она располагается в первой четверти. То есть в первой четверти \(a>0\), а в третьей \(a<0\) (но такие же по модулю).
Поэтому рассмотрим только первую четверть.

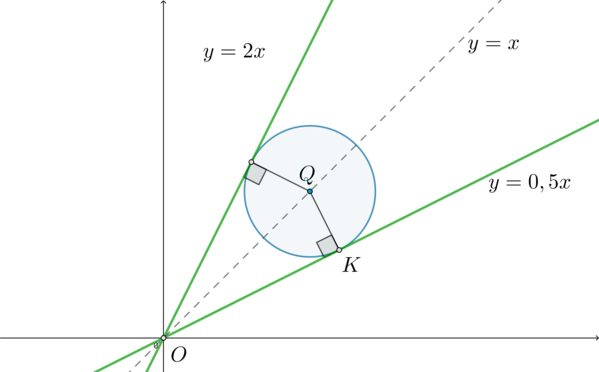
Заметим, что \(OQ=\sqrt{(a-0)^2+(a-0)^2}=\sqrt2a\), \(QK=R=\sqrt5a^2\). Тогда \[OK=\sqrt{2a^2-5a^4}\] Тогда \[\mathrm{tg}\,\angle QOK=\dfrac{\sqrt5a^2}{\sqrt{2a^2-5a^4}}\] Но, с другой стороны, \[\mathrm{tg}\,\angle QOK=\mathrm{tg}\,(45^\circ-\alpha)=\dfrac{\mathrm{tg}\, 45^\circ-\mathrm{tg}\,\alpha}{1+\mathrm{tg}\,45^\circ\cdot \mathrm{tg}\,\alpha}\] следовательно, \[\dfrac{1-0,5}{1+1\cdot 0,5}=\dfrac{\sqrt5a^2}{\sqrt{2a^2-5a^4}} \quad\Leftrightarrow\quad a=\pm \dfrac15\] Таким образом, мы уже сразу получили и положительное, и отрицательное значение для \(a\). Следовательно, ответ: \[a\in \{-0,2;0,2\}\]

Ответ:

\(\{-0,2;0,2\}\)

а) Пусть \(a_1=x\), \(a_2=y\). Тогда \(a_3=x+y, a_4=x+2y, a_5=2x+3y\). Предположим, что выполняется \(4a_5=7a_4\). Тогда: \[4(2x+3y)=7(x+2y)\quad\Leftrightarrow\quad x=2y\] Если взять, например, \(x=2\), \(y=1\), то получим последовательность: \(2, 1, 3, 4, 7, \dots\) Следовательно, такое возможно.

б) Аналогично пункту а): \[5(2x+3y)=7(x+2y)\quad\Leftrightarrow\quad 3x=-y\] Следовательно, один из \(x\) или \(y\) должен быть отрицательным (оба они не могут быть равны \(0\), так как последовательность состоит из натуральных чисел). Но это невозможно, так как последовательность состоит из натуральных чисел. Следовательно, ответ: нет.

в) Отметим основные свойства последовательности, где \(a_{n+1}=a_n+a_{n-1}\) при натуральных \(n\geqslant 2\). Заметим, что первые два элемента этой последовательности задаются произвольно, а вот каждый следующий, начиная с третьего, равен сумме двух предыдущих. Следовательно, так как последовательность состоит из натуральных чисел, то каждый элемент, начиная с третьего, больше предыдущего, то есть \(a_{n+1}:a_n>1\) при \(n\geqslant 2\).
Это же свойство можно переформулировать по-другому: каждый элемент, начиная со второго, меньше следующего: \(a_n:a_{n+1}<1\) при \(n\geqslant 2\).
Но тогда \[\dfrac{a_{n+1}}{a_n}=1+\dfrac{a_{n-1}}{a_n}<1+1=2, \quad n\geqslant 3\] (каждый элемент, начиная с 4-ого, менее чем в два раза больше предыдущего)

Предположим, что равенство \(6na_{n+1}=(n^2+24)a_n\) вплоть до какого-то большого \(n\) (то есть \(n\geqslant 3\)). Тогда \[\dfrac{a_{n+1}}{a_n}=\dfrac{n^2+24}{6n}<2\] Решим неравенство: \[\dfrac{n^2+24}{6n}<2\quad\Rightarrow\quad n^2-12n+24<0 \quad\Leftrightarrow\quad n\in (6-\sqrt{12};6+\sqrt{12})\] Так как \(n\) – натуральное, а \(9<6+\sqrt{12}<10\), то \(n\leqslant 9\).
Следовательно, наибольший элемент, для которого может быть выполнено равенство из пункта в), это \(a_{10}\).
Попробуем привести пример. Для этого нам понадобиться равенство \(a_{n+2}=a_{n+1}+a_n\) использовать в виде \(a_n=a_{n+2}-a_{n+1}\), а также то, что каждый элемент последовательности, начиная с третьего, должен быть больше предыдущего.

Пусть \(n=9\). Тогда \[\begin{aligned} &6\cdot 9\cdot a_{10}=105a_9\\ &18a_{10}=35a_9\quad\Rightarrow\\ &a_{10}=35k\\ &a_9=18k\\ &a_8=17k\\ &a_7=k\\ &a_6=16k\end{aligned}\] Получили, что \(a_6>a_7\) – противоречие.

Пусть \(n=8\). Тогда \[\begin{aligned} &6\cdot 8\cdot a_9=88a_8\\ &6a_9=11a_8\quad\Rightarrow\\ &a_9=11k\\ &a_8=6k\\ &a_7=5k\\ &a_6=k\\ &a_5=4k\end{aligned}\] Получили противоречие.

Пусть \(n=7\). Тогда \[\begin{aligned} &6\cdot 7\cdot a_8=73a_7\quad\Rightarrow\\ &a_8=73k\\ &a_7=42k\\ &a_6=31k\\ &a_5=11k\\ &a_4=20k\end{aligned}\] Получили противоречие.

Пусть \(n=6\). Тогда \[\begin{aligned} &6\cdot 6\cdot a_7=60a_6\\ &3a_7=5a_6\quad\Rightarrow\\ &a_7=5k\\ &a_6=3k\\ &a_5=2k\\ &a_4=k\\ &a_3=k\end{aligned}\] Получили противоречие.

Пусть \(n=5\). Тогда \[\begin{aligned} &6\cdot 5\cdot a_6=49a_5\quad\Rightarrow\\ &a_6=49k\\ &a_5=30k\\ &a_4=19k\\ &a_3=11k\\ &a_2=8k\\ &a_1=3k\end{aligned}\] Противоречия нет, следовательно, наибольшее возможное \(n\) – это \(n=5\). Пример: \(3; 8; 11; 19; 30; 49\).

Ответ:

а) да

б) нет

в) 5