Дана треугольная пирамида \(SABC\), причем грани \(SAB\) и \(SAC\) представляют собой равные равнобедренные треугольники с прямыми углами при вершине \(A\). Найдите расстояние от точки \(A\) до грани \(SBC\), если высота пирамиды равна \(h\) и равна \(BC\).
Из условия задачи следует, что:
1) \(SA\perp AB, AC \Rightarrow SA\perp (ABC)\);
2) \(SA=AB=AC=h=BC\);
3) \(SB=SC=h\sqrt2\).
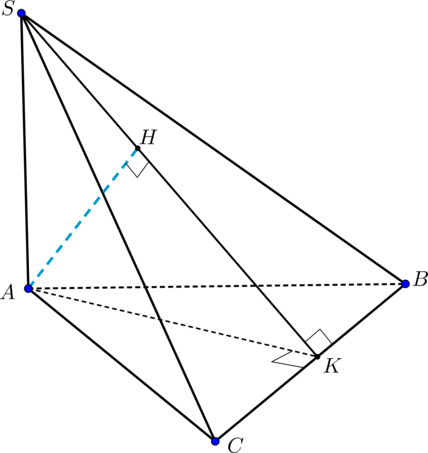
Т.к. \(\triangle BAC\) равнобедренный, то \(AK\perp BC, K\) – середина \(BC\). Аналогично, \(SK\perp BC\). Таким образом, перпендикуляр \(AH\) на плоскость \(SBC\) упадет на прямую \(SK\) (удовлетворяет теореме о трех перпендикулярах: \(HK\) – проекция, \(AK\) – наклонная, обе перпендикулярны \(BC\)).
По теореме Пифагора \(AK=\dfrac{h\sqrt3}{2}\).
Следовательно, \(\mathrm{tg}\, \angle
SKA=\dfrac{SA}{AK}=\dfrac{2\sqrt3}{3}=\dfrac{AH}{HK}\).
Значит, \(AH=2\sqrt3x, HK=3x\).
По теореме Пифагора из \(\triangle AHK\) находим \(x=\dfrac{1}{2\sqrt7}h \Rightarrow AH=\sqrt{\dfrac{3}{7}}h\)
Ответ:
\(\sqrt{\dfrac{3}{7}}h\)