Окружность проходит через вершины \(A, B\) и \(D\) параллелограмма \(ABCD\). Эта окружность пересекает \(BC\) в точке \(E\), а \(CD\) в точке \(K\).
а) Докажите, что отрезки \(AE\) и \(AK\) равны.
б) Найдите \(AD\), если известно, что \(EC=48\), \(DK=20\), а косинус угла \(BAD\) равен \(0,4\).
(ЕГЭ 2018, основная волна)
а) 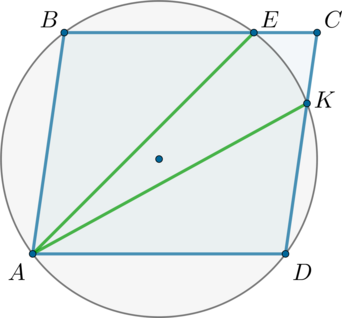
Так как противоположные углы параллелограмма равны, то \(\angle
ABE=\angle ADK\). Так как равные вписанные углы опираются на равные дуги и на равные хорды, то \(AE=AK\), чтд.
б) Введем обозначения: \(AD=x\), \(CK=y\). Проведем отрезок \(ED\). Тогда \(ABED\) – трапеция, причем, так как она вписана в окружность, она равнобедренная. Следовательно, \(ED=y+20\).
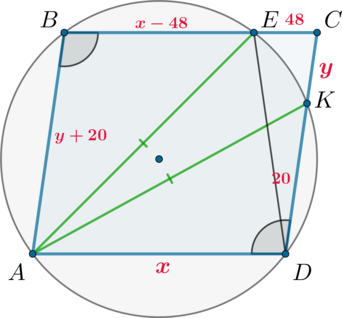
Запишем теорему косинусов для \(\triangle ECD\): \[(y+20)^2=48^2+(y+20)^2-2\cdot 48\cdot (y+20)\cdot 0,4
\quad\Rightarrow\quad y=40\] Следовательно, \(AB=60\).
Так как \(\angle B+\angle C=180^\circ\) по свойству параллелограмма, то их косинусы противоположны, следовательно, \(\cos \angle
B=-0,4\).
Так как \(AE=AK\), то найдем \(AE^2\) и \(AK^2\) по теореме косинусов из \(\triangle ABE\) и \(\triangle ADK\) и приравняем: \[60^2+(x-48)^2-2\cdot 60\cdot (x-48)\cdot (-0,4)=x^2+20^2-2\cdot 20\cdot x
\cdot (-0,4) \quad\Rightarrow\quad x=50\] Следовательно, \(AD=50\).
Ответ:
б) 50