Задачи на нахождение касательной

Графиком \(f(x)\) является парабола, пересекающая ось \(Ox\) в точках \(x=-3\) и \(x=1\), а ось \(Oy\) в точке \(y=-3\).

Графиком \(ay+5x+6a=0\) при каждом фиксированном \(a\) является прямая:

1) При \(a=0\) это прямая \(x=0\). Она имеет ровно одну точку пересечения с \(f(x)\), а именно, точку \((0;-3)\).

2) При \(a\ne 0\) это пучок прямых \(y=-\dfrac{5}{a}x-6\), проходящих через точку \((0;-6)\).

Графики будут иметь ровно 1 точку пересечения при тех значениях \(a\), при которых прямая \(y\) будет касаться параболы.

Условия касания в точке \(x_o\): \[\begin{cases} f'(x_o)=-\dfrac{5}{a}\\ f(x_o)=y(x_o) \end{cases} \Rightarrow \begin{cases} x_o=-\dfrac{5}{2a}-1\\ 8a^2-20a-25=0 \end{cases} \Rightarrow a=\dfrac{5}{4}(1 \pm \sqrt3)\]

Ответ:

\(a\in \Big\{ \dfrac{5}{4}(1-\sqrt3); \ 0; \ \dfrac{5}{4}(1+\sqrt3)\Big\}\).

Рассмотрим функцию \(f(x)=\dfrac{1}{3}x^3+2x^2-\dfrac{88}{3}\) и пучок прямых \(y=a(x+8)\).

\(f'(x)=x^2+4x \Rightarrow x=-4=x_{max}\) – точка максимума, \(x=0=x_{min}\) – точка минимума.

\(f(x_{max})=-\dfrac{56}{3}, \ \ f(x_{min})=-\dfrac{88}{3}\).

Все прямые \(y=ax+8a\) проходят через точку \((-8;0)\).

Найдем случаи, когда прямая \(y\) касается графика функции \(f(x)\) (\(x_o\) – точка касания). Найдем соответствующие этому значения параметра: \[\begin{cases} f'(x_o)=a\\ f(x_o)=y(x_o) \end{cases} \Rightarrow \begin{cases} x_o^2+4x_o=a\\ 2x_o^3+30x_o^2+96x_o+88=0 \end{cases}\Rightarrow \begin{cases} x_o^2+4x_o=a\\ (x_o+2)^2(x_o+11)=0 \end{cases} \Rightarrow \left[ \begin{gathered} \begin{aligned} &\begin{cases} x_o=-2\\ a=-4 \end{cases}\\ &\begin{cases} x_o=-11\\ a=77 \end{cases} \end{aligned} \end{gathered} \right.\]

Таким образом, уравнение \(f(x)=y\) будет иметь единственное значение при тех значениях \(a\), при которых прямые \(y\) будут располагаться в закрашенных областях: (причем граничный случай \(a=77\) не подходит)

В уменьшенном масштабе это выглядит так:

Следовательно, \(a\in (-\infty; 77)\).

Ответ:

\(a\in (-\infty; 77)\).

1) Первое уравнение системы при \(a\ne 0\) задает отрезок \(BC\), где \(B(a;0)\), \(C(0;-a)\).
Действительно, пусть \(A(x;y)\). Тогда \[\begin{aligned} &BA=\sqrt{(x-a)^2+y^2}\\[1ex] &AC=\sqrt{x^2+(y+a)^2}\\[1ex] &BC=\sqrt{(a-0)^2+(0+a)^2}=|a\sqrt2| \end{aligned}\] Таким образом, первое уравнение можно записать в виде \[BA+AC=BC\] То есть данное уравнение задает множество точек \(A\), лежащих на отрезке \(BC\).
При \(a=0\) данное уравнение задает единственную точку \(O(0;0)\).

2) Второе неравенство задает круг с центром в точке \(O(0;0)\) и радиусом \(R=3\sqrt2\).

3) Для того, чтобы данная система имела единственное решение при \(a\ne 0\), нужно, чтобы отрезок касался круга: при \(a>0\) отрезок \(BC\) будет находиться в четвертой четверти (рисунок 1), при \(a<0\) – во второй (рисунок 2).
Случай, когда \(a=0\), нам также подходит (так как точка \(O\) принадлежит кругу).



При \(a>0\): \(BO=CO=|a|=a, OK=3\sqrt2\) – радиус, проведенный в точку касания. Тогда \[\dfrac12\cdot OB\cdot OC=S_{\triangle OBC}=\dfrac12\cdot OK\cdot BC \quad\Rightarrow\quad a\cdot a=3\sqrt2\cdot a\sqrt2 \quad\Rightarrow\quad a=6.\] При \(a<0\): \(BO=CO=|a|=-a\). Тогда \[\dfrac12\cdot OB\cdot OC=S_{\triangle OBC}=\dfrac12\cdot OK\cdot BC \quad\Rightarrow\quad -a\cdot (-a)=3\sqrt2\cdot (-a\sqrt2) \quad\Rightarrow\quad a=-6.\]

Ответ:

\(a\in \{-6;0;6\}\)

Пусть \(y=3x^3+ax+5\). Рассмотрим несколько случаев:

1) \(a=0\). Тогда уравнение имеет единственное решение \(x=-\sqrt[3]{\dfrac{5}{3}}\).

2) \(a>0\). Найдем производную \(y'=9x^2+a\). Т.к. \(a>0\), то \(y'>0\) при любых \(x\). Следовательно, функция \(y\) монотонно возрастает на всем \(\mathbb{R}\). Значит, имеет не более одной точки пересечения с осью \(Ox\).

Заметим, что \(y\left(-\dfrac{5}{a}\right)=-\dfrac{375}{a^3}<0; \ \ y(0)=5>0\), следовательно, на промежутке \(\left(-\dfrac{5}{a};0\right)\) есть точка \(x_o\), в которой \(y(x_o)=0\). Значит, \(x_o\) и есть единственное решение данного уравнения.

3) \(a<0\). Обозначим \(-a=b>0\).

Рассмотрим уравнение в виде \(3x^3=bx-5\). Обозначим \(f(x)=3x^3, \ g(x)=bx-5\). Найдем положительные значения \(b\), при которых функции \(f(x)\) и \(g(x)\) имеют ровно одну точку пересечения.

Найдем значения \(b\), при которых \(g(x)\) касается \(f(x)\):

\(f'(x)=9x^2\). Пусть \(x_o\) – точка касания. Тогда: \[\begin{cases} b>0\\ f'(x_o)=b\\ f(x_o)=g(x_o) \end{cases} \Rightarrow b=9\sqrt[3]{\dfrac{25}{36}}\]

Значит, при \(b=9\sqrt[3]{\dfrac{25}{36}}\) функции \(f(x)\) и \(g(x)\) имеют 2 точки пересечения, а при \(0<b<9\sqrt[3]{\dfrac{25}{36}}\) функции \(f(x)\) и \(g(x)\) имеют ровно одну точку пересечения (например, прямая, обозначенная пунктиром).

Тогда \(-9\sqrt[3]{\dfrac{25}{36}}<a<0\).

Значит, уравнение будет иметь единственный корень при \(a\in \left(-9\sqrt[3]{\dfrac{25}{36}}; +\infty\right)\).

Ответ:

\(a\in \left( -9\sqrt[3]{\dfrac{25}{36}}; +\infty \right)\).

Вопрос можно переформулировать следующим образом: неравенство \[4ax+|x^2-6x+5|>-24\] должно выполняться при всех \(x\) из ОДЗ (а ОДЗ: \(x\in \mathbb{R}\)).
Перепишем неравенство в виде \[|x^2-6x+5|>-4ax-24\qquad (*)\] и рассмотрим функции \(g(x)=|x^2-6x+5|\) и \(h(x)=-4ax-24\). Тогда для того, чтобы неравенство \((*)\) было выполнено при всех \(x\), нужно, чтобы прямая \(h\) находилась ниже графика функции \(g\).

1) Рассмотрим случай, когда \(b=-4a>0\). Пусть прямая \(h\) касается правой ветви параболы \(y=x^2-6x+5\) (при \(x\geqslant 5\)).

\(y'=2x-6\). Следовательно, если они касаются в точке с абсциссой \(x_0\), то \[2x_0-6=b \quad {\small{\text{и}}} \quad x_0^2-6x_0+5=bx_0-24\] Из этих двух уравнений находим, учитывая \(x\geqslant 5\), что \(x_0=\sqrt{29}\).
Следовательно, при \(x_0=\sqrt{29}\) имеем \(b=2(\sqrt{29}-3)\).
Тогда при всех \(0<b<2(\sqrt{29}-3)\) прямая будет находиться ниже графика \(g\), следовательно, для всех \(x\) будет выполнено неравенство \((*)\).

2) Рассмотрим случай, когда \(b=0\). Тогда прямая \(h(x)=-24\) параллельна оси абсцисс и находится ниже графика \(g\) при всех \(x\). Следовательно, это значение \(b\) нам подходит.

3) Рассмотрим случай, когда \(b<0\). Пусть прямая \(h\) касается левой ветви параболы \(y=x^2-6x+5\) (при \(x\leqslant 1\)).

\(y'=2x-6\). Следовательно, если они касаются в точке с абсциссой \(x_0\), то \[2x_0-6=b \quad {\small{\text{и}}} \quad x_0^2-6x_0+5=bx_0-24\] Из этих двух уравнений находим, учитывая \(x\leqslant 1\), что \(x=-\sqrt{29}\). Отсюда находим, что \(b=-2(\sqrt{29}-3)\).

Следовательно, при всех \(-2(\sqrt{29}+3)<b<0\) прямая \(h\) будет находиться ниже графика \(g\) и неравенство будет выполнено при всех \(x\).

Итого заключаем, что нам подходят значения: \[-2(\sqrt{29}+3)<b<2(\sqrt{29}-3) \quad\Rightarrow\quad -\dfrac{\sqrt{29}-3}2<a<\dfrac{\sqrt{29}+3}2\]

Прямые \(h\) должны находиться в зеленой области.

Ответ:

\(-\dfrac{\sqrt{29}-3}2<a<\dfrac{\sqrt{29}+3}2\)

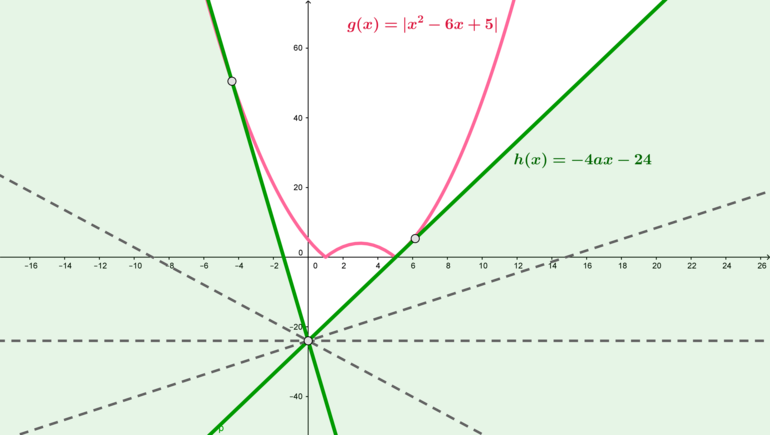
Перепишем неравенство в виде: \[2|x-a|+a\leqslant -x^2+4x\]

Пусть \(f(x)=2|x-a|+a\), \(g(x)=-x^2+4x\) – функции. Тогда по условию задачи необходимо, чтобы промежуток, для которого график \(f\) лежит не выше графика \(g\), содержал ровно одну целую точку.

Заметим, что графиком функции \(f\) является уголок, вершина которого скользит по прямой \(y=x\). Правая ветвь уголка задается уравнением \(f_1(x)=2(x-a)+a=2x-a\) при \(x\geqslant a\); левая ветвь — \(f_2(x)=-2(x-a)+a=-2x+3a\) при \(x<a\).

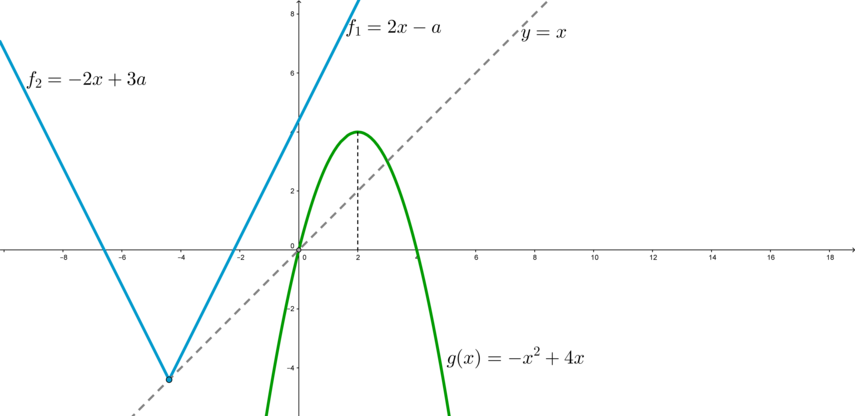
1) Найдем значение параметра, при котором правая ветвь уголка касается параболы (т.к. если уголок находится левее этого положения, то неравенство не имеет решений).
\(g'=-2x+4\). Если \(f_1\) касается \(g\) в точке \(x_0\), то \(g'(x_0)\) равно коэффициенту при \(x\) в уравнении \(f_1\), то есть:

\[-2x_0+4=2 \quad \Rightarrow \quad x_0=1\]

Т.к. \(f_1\) касается \(g\), то \(f_1(x_0)=g(x_0)\), откуда находим значение параметра \(a=-1\).

Таким образом, при \(a=-1\) правая ветвь \(f_1\) касается параболы:

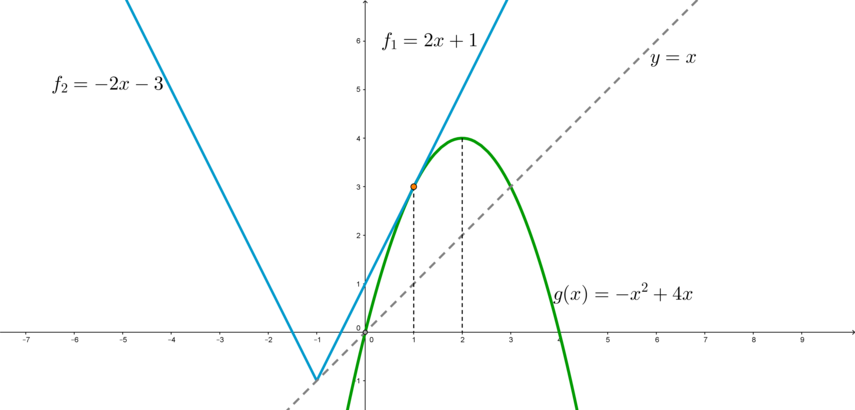
Заметим, что при \(a=-1\) существует ровно одно решение для неравенства, и это \(x=1\), что является целочисленным значением. Следовательно, \(a=-1\) нам подходит.

2) Заметим, что при \(a=0\) вершина уголка находится в точке \((0;0)\) и уголок имеет две точки пересечения с параболой: \(x=0\) и \(x=2\). Следовательно, решением неравенства является отрезок \([0;2]\) (т.к. на этом отрезке уголок находится не выше параболы), содержащий три целых точки (\(0,1\) и \(2\)). А вот при \(a<0\) (но \(a\geqslant -1\)) левая ветвь уголка не пересекает параболу, а правая ветвь пересекает параболу в двух точках, причем одна находится между \(0\) и \(1\), а вторая между \(1\) и \(2\). То есть в промежуток, удовлетворяющий неравенству, будет входить ровно одна целая точка \(x=1\). Следовательно, все \(-1\leqslant a<0\) нам подходят.

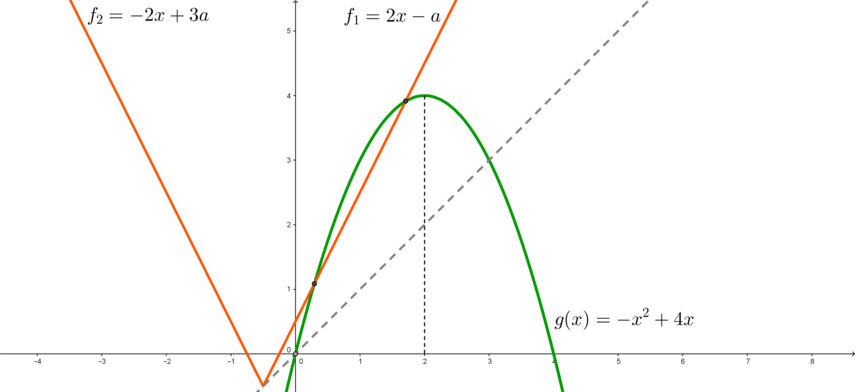
3) Заметим, что если вершина уголка находится в точке \((3;3)\) (то есть \(a=3\)), то левая ветвь уголка касается параболы (в этой точке). Действительно, это можно проверить, поступив так же, как мы поступили в первом пункте: \(g'=-2x+4\). Если \(f_2\) касается \(g\) в точке \(x_0\), то \(g'(x_0)\) равно коэффициенту при \(x\) в уравнении \(f_2\), то есть:

\[-2x_0+4=-2 \quad \Rightarrow \quad x_0=3\]

Следовательно, при \(a=3\) решением неравенства является единственная точка \(a=3\), которая является целой, то есть \(a=3\) нам подходит.

Заметим также, что при \(a>3\) уголок будет находится всегда выше параболы, то есть неравенство не будет иметь решений.

4) Рассмотрим ситуацию, когда \(0<a<3\). При этих \(a\) правая ветвь уголка пересекает параболу в точке \(x\in(2;3)\), а вот левая ветвь пересекает параболу в какой-то точке \(x\in(0;3)\). Следовательно, чтобы неравенство имело единственное целочисленное решение, этим решением должно быть \(x=2\) и точка \(x'\), в которой левая ветвь пересекает параболу, должна удовлетворять: \(1<x'\leqslant 2\)(оранжевый уголок).

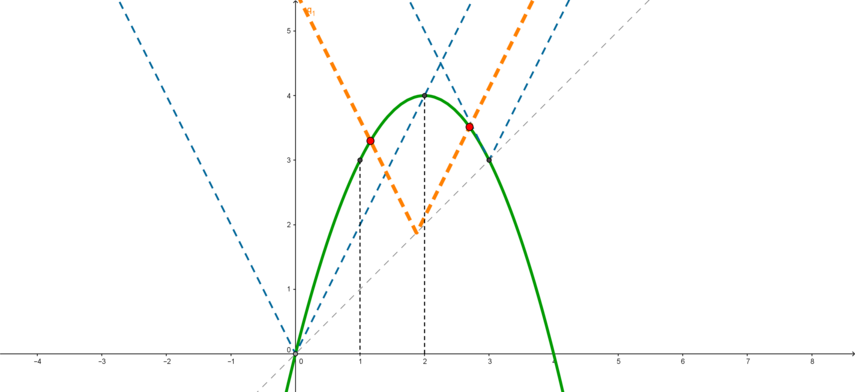
Поэтому найдем значение \(a\), при котором левая ветвь уголка пересекает параболу в точке \(x=1\): \[f_2(1)=g(1) \quad \Rightarrow \quad -2+3a=-1+4 \quad \Rightarrow \quad a=\dfrac53\]

Теперь найдем значение \(a\), при котором левая ветвь уголка пересекает параболу в точке \(x=2\):\[f_2(2)=g(2) \quad \Rightarrow \quad -4+3a=-4+8 \quad \Rightarrow \quad a=\dfrac83\]

То есть при \(a=\frac53\) решением неравенства является отрезок \([1;2,...]\), содержащий 2 целые точки (\(x=1;2\)); при \(a=\frac83\) решением неравенства является отрезок \([2;2,...]\), содержащий одну целую точку (\(x=2\)).

Следовательно, при \(\frac52<a\leqslant \frac83\) решением будет отрезок \([1,...;2,...]\), который содержит одну целую точку \(x=2\). Такие значения \(a\) нам подходят.

Таким образом, итоговый ответ:
при \(-1\leqslant a<0\) целочисленное решение \(x=1\);
при \(\frac53<a\leqslant \frac83\) целочисленное решение \(x=2\);
при \(a=3\) целочисленное решение \(x=3\).

Ответ:

\(a\in [-1;0)\cup\left(\frac53;\frac83\right]\cup\{3\}\)

Рассмотрим первое уравнение системы. Перепишем его в виде: \[\sqrt{(x+1)^2+(y-3)^2}+\sqrt{(x-3)^2+y^2}=5\] Пусть \(A(x;y)\), \(B(-1;3)\), \(C(3;0)\) – точки. Тогда \[\begin{aligned} &BA=\sqrt{(x+1)^2+(y-3)^2} \\[2ex] &AC=\sqrt{(x-3)^2+y^2}\\[2ex] &BC=\sqrt{(-1-3)^2+(3-0)^2}=5 \end{aligned}\] Следовательно, первое уравнение равносильно: \[BA+AC=BC\] Значит, \(A\) – точка, принадлежащая отрезку \(BC\). То есть уравнение задает множество точек отрезка \(BC\).

Рассмотрим второе уравнение. Заметим, что \(x\ne a\), так как в этом случае уравнение принимает вид \(0=1\), что не является верным равенством. Тогда можно переписать уравнение в виде: \[y=\dfrac1{x-a}\] Графиком данной функции при каждом фиксированном \(a\) является гипербола (сдвинутая на \(|a|\) единиц влево/вправо, если \(a<0\)/\(a>0\)).

Заметим, что отрезок \(BC\) находится в верхней полуплоскости, следовательно, только правая ветка гиперболы может его пересекать.
Найдем значения \(a\), при которых гипербола проходит через точку \(B\).



Тогда \[3=\dfrac1{-1-a} \quad\Leftrightarrow\quad a=-\dfrac43.\] Найдем значения \(a\), при которых гипербола касается отрезка \(BC\) в точке \(K(x_0;y_0)\).



Для этого нужно написать уравнение прямой, проходящей через точки \(B, C\). Пусть \(y=kx+b\) – уравнение этой прямой. Тогда \[\begin{cases} 3=-k+b\\ 0=3k+b \end{cases} \quad\Leftrightarrow\quad \begin{cases} k=-\dfrac34\\[2ex] b=\dfrac94 \end{cases} \quad\Rightarrow\quad y=-\dfrac34x+\dfrac94\] Производная функции, задающей гиперболу, равна \[y'=-\dfrac1{(x-a)^2}\] Тогда условие касания задается \[\begin{cases} -\dfrac1{(x_0-a)^2}=-\dfrac34\\[2ex] \dfrac1{x_0-a}=-\dfrac34x_0+\dfrac94 \end{cases} \quad\Leftrightarrow\quad \begin{cases} x_0=3-\dfrac2{\sqrt3}\\[2ex] a=3-\dfrac4{\sqrt3} \end{cases}\] Следовательно, при \[a\in \left[-\dfrac43;3-\dfrac4{\sqrt3}\right)\] гипербола будет иметь с отрезком \(BC\) равно две точки пересечения.

Ответ:

\(a\in \left[-\frac43;3-\frac4{\sqrt3}\right)\)