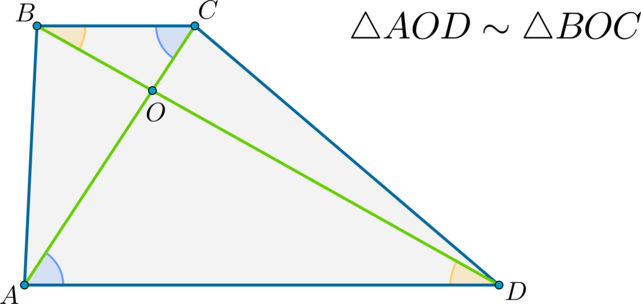
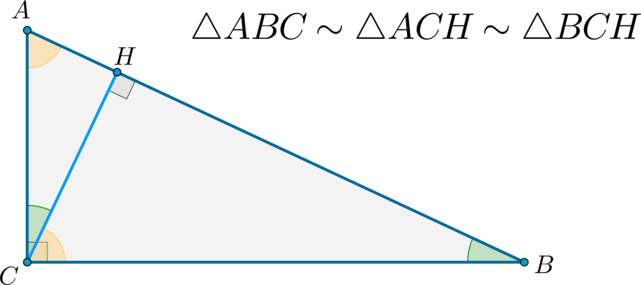
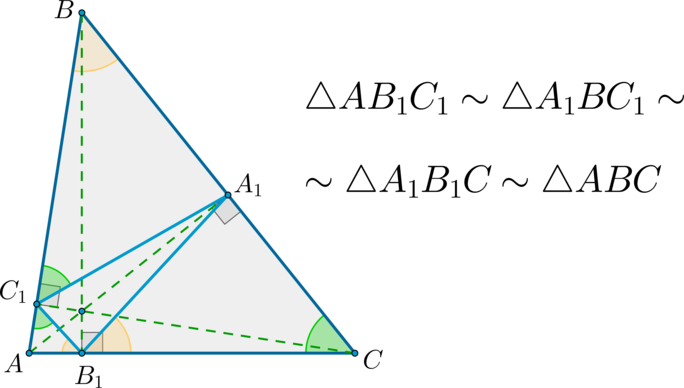
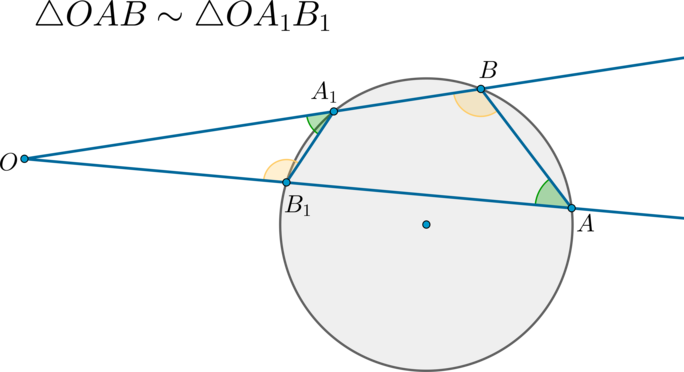
В квадрате \(ABCD\) на стороне \(CD=\sqrt{13}\) взята точка \(K\) такая, что \(DK=\frac23DC\). Найдите расстояние от точки \(B\) до прямой \(AK\).
Обозначим сторону квадрата за \(3x\), тогда \(DK=2x\), \(KC=x\). Необходимо найти \(BH\).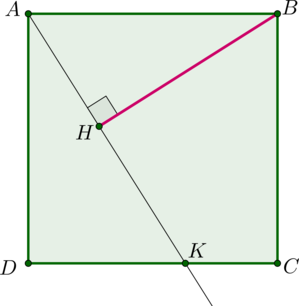
Заметим, что \(\triangle ADK\sim \triangle ABH\) по двум углам (\(\angle ADK=\angle AHB=90^\circ\), \(\angle AKD=\angle HAB\) как накрест лежащие). Следовательно, \[\dfrac{BH}{AD}=\dfrac{AB}{AK}.\] По теореме Пифагора \(AK=\sqrt{AD^2+DK^2}=\sqrt{13}x\), следовательно, \[BH=\dfrac{AD\cdot AB}{AK}=\dfrac{9x^2}{\sqrt{13}x}=\dfrac9{\sqrt{13}}x\] Так как \(AD=\sqrt{13}=3x\), то \(x=\frac{\sqrt{13}}3\), следовательно, \[BH=3.\]
Ответ: 3