Один метр равен десяти дециметрам. Пусть \(m\) длина палки в метрах, а \(d\) – в дециметрах. Найдите \(\dfrac{m}{d}\).
\(m\cdot 1\)м \(= m\cdot 10\)дм \(= d\)дм, откуда \(10\cdot m = d\), то есть \(\dfrac{m}{d} = 0,1\).
Ответ: 0,1
Тренировочные варианты "Школково". Уровень Максим Олегович
Один метр равен десяти дециметрам. Пусть \(m\) длина палки в метрах, а \(d\) – в дециметрах. Найдите \(\dfrac{m}{d}\).
\(m\cdot 1\)м \(= m\cdot 10\)дм \(= d\)дм, откуда \(10\cdot m = d\), то есть \(\dfrac{m}{d} = 0,1\).
Ответ: 0,1
На рисунке жирными точками показана среднесуточная температура в городе Москве с 13 по 27 марта. По горизонтали указывается день месяца, по вертикали – среднесуточная температура в соответствующий день, в градусах Цельсия. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку разницу между максимальной и минимальной среднесуточными температурами в указанный период.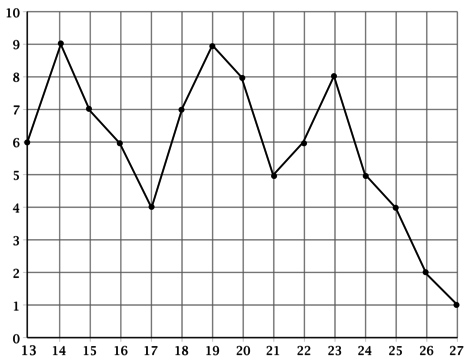
По рисунку видно, что в указанный период максимальная температура составляла 9 градусов Цельсия, а минимальная 1 градус Цельсия. Разница: \(9 - 1 = 8\) градусов Цельсия.
Ответ: 8
Прямая \(AB\) касается окружности в точке \(A\). На окружности отмечена точка \(C\) так, что \(CB\perp AB\) и \(CB=AB\). Найдите центральный угол, опирающийся на меньшую дугу \(AC\). Ответ дайте в градусах.
Рассмотрим картинку: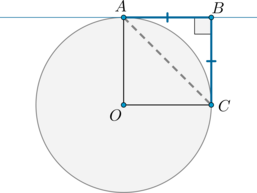
Треугольник \(ABC\) – равнобедренный и прямоугольный, следовательно, \(\angle BAC=45^\circ\). Т.к. угол между касательной \(AB\) и хордой \(AC\) равен половине дуги \(\buildrel\smile\over{AC}\), заключенной между ними, то \(\buildrel\smile\over{AC}=90^\circ\). Тогда центральный угол \(\angle AOC=\buildrel\smile\over{AC}=90^\circ\).
Ответ: 90
Известно, что в множестве \(M\) ровно 100 натуральных чисел, из которых 10 делятся на 2, 15 делятся на 3, 1 делится на 6. Какова вероятность наугад выбрать число из \(M\), которое делится хотя бы на одно из чисел 2 и 3?
Вероятность наступления по крайней мере одного из двух событий равна сумме вероятностей этих событий минус вероятность их одновременного наступления, тогда искомая вероятность равна \[\dfrac{10}{100} + \dfrac{15}{100} - \dfrac{1}{100} = 0,24.\]
Ответ: 0,24
Найдите положительный корень уравнения \((x^2+1)^2-6x^2-1=0\).
Сделаем замену: \(x^2+1=t\). Тогда \(x^2=t-1\) и уравнение примет вид: \[t^2-6(t-1)-1=0\quad\Leftrightarrow\quad t^2-6t+5=0\] По теореме Виета корнями являются числа \(t=5\) и \(t=1\), следовательно, \[\left[\begin{gathered}\begin{aligned} &x^2+1=1\\&x^2+1=5 \end{aligned}\end{gathered}\right.\quad\Leftrightarrow\quad \left[\begin{gathered}\begin{aligned} &x^2=0\\&x^2-4=0 \end{aligned}\end{gathered}\right.\quad\Leftrightarrow\quad \left[\begin{gathered}\begin{aligned} &x=0\\&(x-2)(x+2)=0 \end{aligned}\end{gathered}\right.\quad\Leftrightarrow\quad \left[\begin{gathered}\begin{aligned} &x=0\\&x=2\\&x=-2 \end{aligned}\end{gathered}\right.\] Следовательно, положительный корень – это \(x=2\).
Ответ: 2
Дан треугольник \(ABC\). На сторонах \(AB\) и \(BC\) отмечены точки \(A'\) и \(C'\) соответственно. Известно, что \(BC'=0,5BC=4\), \(AB=14\), \(S_{ABC}=7S_{A'BC'}\). Найдите \(A'B\).
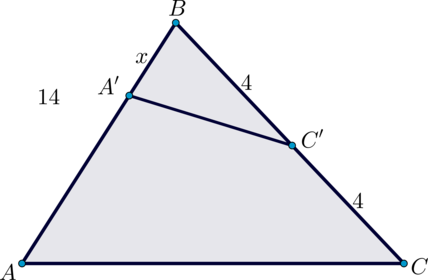
Площадь треугольника \(ABC\) равна \(S_{ABC}=0,5\cdot 14 \cdot 8\cdot \sin\angle B\).
Площадь треугольника \(A'BC'\) равна \(S_{A'BC'}=0,5\cdot A'B\cdot 4\cdot \sin\angle B\).
Таким образом, имеем равенство:
\[0,5\cdot 14 \cdot 8\cdot \sin\angle B=7\cdot 0,5\cdot A'B\cdot 4\cdot \sin\angle B \quad \Leftrightarrow \quad A'B=4.\]
Ответ: 4
На рисунке изображен график функции \(y = f(x)\), определенной на интервале \((-2,4; 8,7)\). Найдите сумму точек экстремума этой функции на отрезке \([1;6]\).
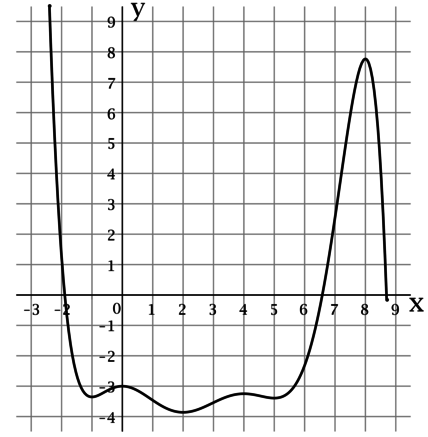
Точкой экстремума функции называется точка, в которой функция достигает локально минимальное или локально максимальное значение.
По рисунку можно определить, что функция \(f(x)\) достигает локально минимальные значения в точках \(-1\), \(2\) и \(5\), а локально максимальные значения в точках \(0\), \(4\) и \(8\). Из них отрезку \([1;6]\) принадлежат точки \(2; 4\) и \(5\). Таким образом, сумма точек экстремума этой функции на отрезке \([1;6]\) равна \(2 + 4+5 = 11\).
Ответ: 11
Дана пирамида \(SABCD\), в основании которой лежит равнобедренная трапеция с основаниями \(AD\) и \(BC\), причем \(AB=BC=CD=4\), а высота \(SO=2\sqrt3\) падает в точку пересечения диагоналей основания. Найдите площадь сечения пирамиды плоскостью, проходящей через диагональ основания перпендикулярно основанию, если известно, что угол при большем основании \(AD\) равен \(60^\circ\).
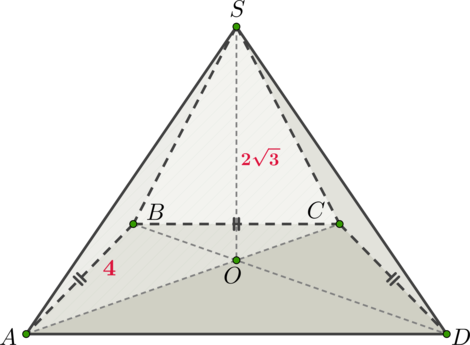
Так как трапеция равнобедренная, то диагонали равны. Плоскость будет перпендикулярна плоскости основания, если будет проходить через прямую, перпендикулярную основанию. Так как \(SO\) – высота пирамиды, то \(SO\perp (ABC)\), следовательно, плоскость, проходящая через \(AC\) и \(SO\), является искомой.
Сечением пирамиды этой плоскостью является треугольник \(ASC\), в котором \(SO\) является высотой.
Так как угол при большем основании трапеции равен \(60^\circ\), то \(\angle ABC=120^\circ\). Тогда по теореме косинусов \[AC^2=AB^2+BC^2-2\cdot AB\cdot BC\cdot \cos120^\circ=48 \quad\Rightarrow
\quad AC=4\sqrt3.\] Следовательно, \[S_{ASC}=\dfrac12\cdot AC\cdot SO=\dfrac12\cdot 4\sqrt3\cdot 2\sqrt3=12.\]
Ответ: 12
Найдите значение выражения \(\displaystyle \frac{a - \sqrt{ab}}{\sqrt{a} - \sqrt{b}}\) при \(a = 0,64\), \(b = 2,25\).
\[\frac{a - \sqrt{ab}}{\sqrt{a} - \sqrt{b}} = \frac{(\sqrt{a})^2 - \sqrt{a}\sqrt{b}}{\sqrt{a} - \sqrt{b}} = \frac{\sqrt{a}(\sqrt{a} - \sqrt{b})}{\sqrt{a} - \sqrt{b}} = \sqrt{a} = \sqrt{0,64} = 0,8\]
Ответ: 0,8
Объем спроса \(Q\) единиц в месяц на продукцию предприятия \(M\) зависит от цены \(P\) в тыс. руб. по формуле \(Q(P) = 55 - P\). Месячная выручка \(R\) в тыс. руб. предприятия \(M\) вычисляется по формуле \(R = P\cdot Q\). Определите наибольшую цену \(P\), при которой месячная выручка \(R\) окажется не менее \(250\) тыс. руб. Ответ дайте в тыс. руб.
\[R = P\cdot Q = 55P - P^2.\] Месячная выручка составит не менее \(250\) тыс. руб. при цене \(P\), которая может быть найдена из неравенства \[55P - P^2 \geq 250\qquad\Leftrightarrow\qquad P^2 - 55P + 250 \leq 0.\] Решим это неравенство методом интервалов. Найдём корни уравнения \(P^2 - 55P + 250 = 0\): \[P_1 = 5,\qquad\qquad P_2 = 50,\] тогда:
то есть наибольшая цена, при которой месячная выручка составит не менее \(250\) тыс. руб., равна 50 тыс. руб.
Ответ: 50
В понедельник \(10\) числа крутого календаря батон подорожал на \(10\%\). Во вторник батон подешевел на \(10\%\) по сравнению с понедельником. В среду батон снова подорожал на \(10\%\) по сравнению со вторником. В четверг батон снова подешевел на \(10\%\) по сравнению со средой. И так далее. Сегодня выяснилось, что батон дороже, чем он был \(10\) числа (в понедельник) в \(1,0673289\) раз. Какое сегодня число согласно крутому календарю, если в нём по \(30\) дней в каждом месяце?
Пусть \(9\) числа батон стоил \(x\) рублей, тогда в понедельник он стоил \(1,1x\) рублей, во вторник он стоил \(1,1x\cdot 0,9 = 0,99x\) рублей, то есть за два дня после \(9\) числа батон подешевел. Аналогично, за четыре дня после \(9\) числа батон подешевел и т.д.
Таким образом, чтобы батон подорожал, после \(9\) числа могло пройти только нечётное количество дней. При этом за любые два дня, первый из которых – чётное число, стоимость батона умножалась на \(0,99\), тогда \[0,99^n\cdot 1,1\cdot x = 1,0673289 x\,,\] откуда находим, что \(n = 3\), то есть прошло \(3\) пары дней и ещё один, тогда сегодня \(16\) число крутого календаря.
Ответ: 16
Найдите точку максимума функции \(y = x\cdot\dfrac{x + 2}{e^x} + \dfrac{1}{e^x}\) на промежутке \([0; 2]\).
ОДЗ: \(x\) – произвольный.
1)
\[\begin{aligned} y' = &\dfrac{x + 2}{e^x} + x\cdot\dfrac{e^x - e^x(x + 2)}{e^{2x}} - \dfrac{1}{e^x} = \dfrac{x + 2}{e^x} + x\cdot\dfrac{1 - (x + 2)}{e^{x}} - \dfrac{1}{e^x} = \dfrac{1 -x^2}{e^x} \end{aligned}\]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна \(0\) или не существует): \[\dfrac{1 -x^2}{e^x} = 0\qquad\Leftrightarrow\qquad \left[ \begin{gathered} x = -1\\ x = 1 \end{gathered} \right.\] Производная существует при любом \(x\).
2) Найдём промежутки знакопостоянства \(y'\):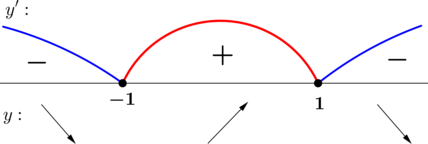
3) Найдём промежутки знакопостоянства \(y'\) на рассматриваемом промежутке \([0; 2]\):
4) Эскиз графика на промежутке \([0; 2]\):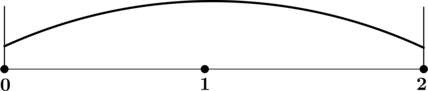
Таким образом, \(x = 1\) – точка максимума функции \(y\) на \([0; 2]\).
Ответ: 1
а) Решите уравнение \[\sin^4x-\cos^4x=\dfrac12\]
б) Укажите все его корни, принадлежащие промежутку \(\left(-\dfrac{\pi}4; \dfrac{11\pi}4\right)\).
а) Применим формулу разности квадратов \(a^2-b^2=(a-b)(a+b)\) для левой части:
\((\sin^2x+\cos^2x)(\sin^2x-\cos^2x)=\dfrac12 \quad \Rightarrow \quad \sin^2x-\cos^2x=\dfrac12 \quad \Rightarrow \quad -\cos2x=\dfrac12 \quad \Rightarrow\)
\(\Rightarrow \quad \cos2x=-\dfrac12 \quad \Rightarrow \quad 2x=\pm \dfrac{2\pi}3+2\pi n, n\in\mathbb{Z} \quad \Rightarrow \quad x=\pm\dfrac{\pi}3+\pi n, n\in\mathbb{Z}\)
б) Отберем корни:
\[-\dfrac{\pi}4<\dfrac{\pi}3+\pi n_1<\dfrac{11\pi}4 \quad \Rightarrow \quad
-\dfrac7{12}<n_1<\dfrac{29}{12}\]
Среди целых чисел подходят \(n_1=0;1;2\), при которых получаются корни \(x=\dfrac{\pi}3; \
\dfrac{4\pi}3; \
\dfrac{7\pi}3\).
\[-\dfrac{\pi}4<-\dfrac{\pi}3+\pi n_2<\dfrac{11\pi}4 \quad \Rightarrow \quad
\dfrac1{12}<n_2<\dfrac{37}{12}\]
Среди целых чисел подходят \(n_2=1;2;3\), при которых получаются корни \(x=\dfrac{2\pi}3; \
\dfrac{5\pi}3; \ \dfrac{8\pi}3\).
Ответ:
а) \(\pm \dfrac{\pi}3+\pi n, n\in\mathbb{Z}\)
б) \(\dfrac{\pi}3; \dfrac{2\pi}3; \dfrac{4\pi}3; \dfrac{5\pi}3; \dfrac{7\pi}3; \dfrac{8\pi}3\)
В кубе \(ABCDA_1B_1C_1D_1\) все ребра равны \(5\). На его ребре \(BB_1\) отмечена точка \(K\) так, что \(KB=3\). Через точки \(K\) и \(C_1\) проведена плоскость \(\alpha\), параллельная прямой \(BD_1\).
а) Докажите, что \(A_1P:PB_1=1:2\), где \(P\) – точка пересечения плоскости \(\alpha\) с ребром \(A_1B_1\).
б) Найдите угол наклона плоскости \(\alpha\) к плоскости грани \(BB_1C_1C\).
а) Прямая параллельна плоскости, если плоскость содержит прямую, параллельную данной. Поэтому проведем в плоскости \(BB_1D_1\), содержащей \(BD_1\), прямую \(KN\parallel BD_1\). Пусть \(N\) – точка пересечения с отрезком \(B_1D_1\).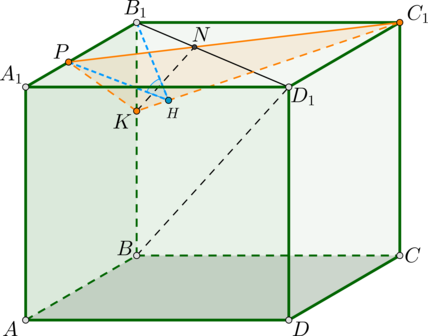
Соединив точки \(C_1\) и \(N\), получим прямую, пересекающую \(A_1B_1\) в точке \(P\).
Т.к. \(KN\parallel BD_1\), то по теореме Фалеса
\[\dfrac{B_1N}{ND_1}=\dfrac{B_1K}{KB}=\dfrac23.\]
Теперь рассмотрим грань \(A_1B_1C_1D_1\). \(\triangle NB_1P\sim \triangle ND_1C_1\), следовательно,
\[\dfrac{PB_1}{C_1D_1}=\dfrac{B_1N}{ND_1}=\dfrac23 \quad \Rightarrow \quad PB_1=\dfrac23C_1D_1=\dfrac23A_1B_1.\]
Следовательно, \(A_1P=\frac13A_1B_1\) и \(A_1P:PB_1=1:2\).
б) Для того, чтобы найти угол между двумя плоскостями, необходимо построить линейный угол двугранного угла, образованного этими плоскостями. Т.к. \(KC_1\) – линия пересечения этих плоскостей, то опустим перпендикуляр \(PH\) на \(KC_1\). По теореме о трех перпендикулярах (\(PB_1\perp (BB_1C_1)\), наклонная \(PH\perp KC_1\)) проекция \(B_1H\perp KC_1\). Следовательно, по определению \(\angle PHB_1\) – линейный угол двугранного угла, образованного данными плоскостями. Его и нужно найти.
Заметим, что \(\triangle PHB_1\) прямоугольный, \(PB_1\) известно, следовательно, найдя \(B_1H\), мы сможем найти тангенс нужного нам угла.
Рассмотрим прямоугольный треугольник \(B_1KC_1\), в котором \(B_1H\) – высота. По теореме Пифагора \(KC_1=\sqrt{KB_1^2+B_1C_1^2}=\sqrt{2^2+5^2}=\sqrt{29}\). Следовательно,
\[S_{B_1KC_1}=\dfrac12KB_1\cdot B_1C_1=\dfrac12B_1H\cdot KC_1 \quad \Rightarrow \quad B_1H=\dfrac{10}{\sqrt{29}}\]
Тогда \[\mathrm{tg}\,\angle PHB_1=\dfrac{PB_1}{B_1H}= \dfrac{\frac{10}3}{\frac{10}{\sqrt{29}}}=\dfrac{\sqrt{29}}3 \quad \Rightarrow \quad \angle PHB_1=\mathrm{arctg}\,\dfrac{\sqrt{29}}3.\]
Ответ:
б) \(\mathrm{arctg}\,\dfrac{\sqrt{29}}3\)
Решите неравенство \[\dfrac 1{2-\log_{1-x^2}{(4x^2-4x+1)}}\leqslant 1\]
Найдем ОДЗ:
\[\begin{aligned}&\begin{cases} 1-x^2>0\\ 1-x^2\ne 1\\ 4x^2-4x+1>0\\ 2-\log_{1-x^2}{(4x^2-4x+1)}\ne 0 \end{cases}\quad\Leftrightarrow\quad \begin{cases} -1<x<1\\ x\ne 0\\ (2x-1)^2>0\\ (2x-1)^2\ne (1-x^2)^2\end{cases}\quad\Leftrightarrow\\[2ex] \Leftrightarrow\quad &\begin{cases} -1<x<1\\ x\ne 0\\ x\ne 0,5\\ 2x-1\ne \pm(1-x^2)\end{cases} \quad\Leftrightarrow\quad \begin{cases} -1<x<1\\ x\ne 0\\ x\ne 0,5\\ x\ne -1\pm\sqrt3; 0; 2\end{cases}\end{aligned}\]
Таким образом, ОДЗ данного неравенства: \(x\in (-1;0)\cup(0;0,5)\cup(0,5;\sqrt3-1)\cup(\sqrt3-1;1)\).
Решим неравенство на ОДЗ. Сделаем замену \(t=2-\log_{1-x^2}{(4x^2-4x+1)}\). Тогда неравенство примет вид:
\[\dfrac 1t\leqslant 1\quad\Leftrightarrow\quad \dfrac{1-t}t\leqslant 0\quad\Leftrightarrow \quad t\in (-\infty;0)\cup[1;+\infty).\]
Сделаем обратную замену:
\[\left[\begin{gathered}\begin{aligned} &2-\log_{1-x^2}{(4x^2-4x+1)}\geqslant 1\\ &2-\log_{1-x^2}{(4x^2-4x+1)}<0 \end{aligned}\end{gathered}\right.\quad\Leftrightarrow\quad \left[\begin{gathered}\begin{aligned} &\log_{1-x^2}{\dfrac{4x^2-4x+1}{1-x^2}}\leqslant 0\\[2ex] &\log_{1-x^2}{\dfrac{4x^2-4x+1}{(1-x^2)^2}}>0 \end{aligned}\end{gathered}\right.\]
Преобразуем каждое из полученных неравенств по методу рационализации:
\[\left[\begin{gathered}\begin{aligned} &(1-x^2-1)\left(\dfrac{4x^2-4x+1}{1-x^2}-1\right)\leqslant 0\\[2ex] &(1-x^2-1)\left(\dfrac{4x^2-4x+1}{(1-x^2)^2}-1\right)>0 \end{aligned}\end{gathered}\right.\quad\Leftrightarrow\quad \left[\begin{gathered}\begin{aligned} &\dfrac{x^3(5x-4)}{(x+1)(x-1)}\leqslant 0\\[2ex] &\dfrac{x^3(x-2)(x^2+2x-2)}{(x-1)^2(x+1)^2}>0 \end{aligned}\end{gathered}\right.\]
Решая каждое неравенство методом интервалов и объединяя решения, мы получим:
\[x\in (-\infty;-\sqrt3-1)\cup(-1;\sqrt3-1)\cup[0,8;1)\cup(2;+\infty).\]
Пересекая данный ответ с ОДЗ, получим окончательный ответ:
\[x\in (-1;0)\cup(0;0,5)\cup(0,5;\sqrt3-1)\cup[0,8;1).\]
Ответ:
\((-1;0)\cup(0;0,5)\cup(0,5;\sqrt3-1)\cup[0,8;1)\)
Две хорды окружности \(AC\) и \(BD\) взаимно перпендикулярны.
а) Найдите отрезок, соединяющий середины хорд \(AC\) и \(BD\), если отрезок, соединяющий точку их пересечения с центром окружности, равен \(3\).
б) При условиях пункта а) найдите \(AD\), если \(AD>BC\), \(AC=BD\) и отрезок, соединяющий середины хорд \(AB\) и \(CD\), равен \(5\).
а) Пусть \(O\) – центр окружности, \(Q\) – точка пересечения хорд \(AC\) и \(BD\). Пусть также \(M\) и \(N\) – середины этих хорд. Тогда \(OM\) и \(ON\) – перпендикуляры к этим хордам.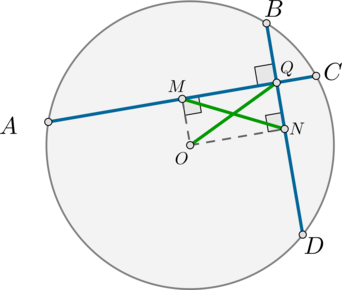
Действительно, \(\triangle AOC\) – равнобедренный (\(OA=OC\) – радиусы), поэтому медиана \(OM\) в нем является и высотой. Аналогично доказывается, что \(ON\perp BD\).
Таким образом, в четырехугольнике \(OMQN\) три угла – прямые (\(\angle M=\angle Q=\angle N=90^\circ\)), следовательно, этот четырехугольник по признаку является прямоугольником. Т.к. в прямоугольнике диагонали равны, то \(MN=OQ=3\).
б) Докажем, что \(ABCD\) – равнобедренная трапеция.
Т.к. \(AC=BD\), то \(\angle ADC=\angle BAD=\alpha\) как вписанные углы, опирающиеся на равные хорды. \(\angle BAC=\angle BDC=\beta\) как вписанные углы, опирающиеся на одну и ту же хорду \(BC\). Таким образом, \(\angle CAD=\angle BDA=\alpha-\beta\). Следовательно, равны и хорды \(AB\) и \(CD\).
Также можно сказать, что \(\angle CAD=\angle BCA\) как вписанные углы, опирающиеся на равные хорды. Следовательно, это накрест лежащие углы при \(AD\) и \(BC\) и \(AC\) – секущей. Значит, по признаку прямые \(AD\parallel BC\). Таким образом, \(ABCD\) – трапеция. А т.к. \(AB=CD\), то она равнобедренная.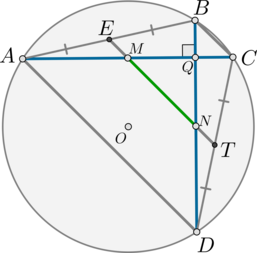
Пусть \(E\) и \(T\) – середины хорд \(AB\) и \(CD\) соответственно, то есть \(ET=5\). Тогда \(ET\) – средняя линия трапеции, следовательно, \(ET\parallel AD\parallel BC\). Тогда по теореме Фалеса прямая \(ET\) пересечет отрезки \(AC\) и \(BD\) также в серединах, следовательно, \(MN\subset ET\).
Обозначим \(AD=x, BC=y\). Тогда \(ET=\frac12\left(x+y\right)\). \(EM\) – средняя линия в \(\triangle BAC\), следовательно, \(EM=\frac12y\). Аналогично \(NT=\frac12y\) как средняя линия в \(\triangle BDC\). Тогда \(MN=ET-EM-NT=\frac12\left(x-y\right)\). Таким образом, имеем систему из двух уравнений:
\[\begin{cases} \frac12\left(x+y\right)=5\\ \frac12\left(x-y\right)=3 \end{cases}\]
Откуда находим, что \(x=AD=8\).
Ответ:
а) 3
б) 8
Банк предоставляет следующие условия по оформлению вкладов:
– два раза в год банк начисляет на вклад некоторый процент;
– в первый год банк начисляет целое кратное десяти число \(y\) процентов;
– в каждый следующий год процент становится в два раза больше процента в предыдущем году.
Найдите \(y\), если известно, что спустя 3 года сумма на счете превысила первоначальную на \(241,5104\%\).
Пусть для определенности банк начисляет проценты в январе и июле. Пусть было положено \(A\) рублей в банк. Составим таблицу: \[\begin{array}{|l|c|c|} \hline \text{Номер года}&\text{Сумма в январе} &\text{Сумма в июле}\\ \hline 1& (1+0,01y)A & (1+0,01y)^2A \\ \hline 2& (1+0,01\cdot 2y)(1+0,01y)^2A & (1+0,01\cdot 2y)^2(1+0,01y)^2A \\ \hline 3& (1+0,01\cdot 4y)(1+0,01\cdot 2y)^2(1+0,01y)^2A & (1+0,01\cdot 4y)^2(1+0,01\cdot 2y)^2(1+0,01y)^2A \\ \hline \end{array}\]
Таким образом, спустя 3 года на счете было \[(1+0,01\cdot 4y)^2(1+0,01\cdot 2y)^2(1+0,01y)^2A \quad {\small{\text{рублей}}}\]
По условию эта сумма превышает первоначальную, то есть \(A\), на \(241,5104\%\). Следовательно, эта сумма составляет \(341,5104\%\) от \(A\). Значит, \[(1+0,01\cdot 4y)^2(1+0,01\cdot 2y)^2(1+0,01y)^2A=3,415104A\] Обозначим \(0,01y=x\) и получим следующее уравнение: \[\Big((1+4x)(1+2x)(1+x)\Big)^2=3,415104\]
Разложим на множители число \(3\,415\,104=2^6\cdot 3^2\cdot 11^2\cdot 7^2\). Следовательно, \(3\,415\,104=(2^3\cdot 3\cdot 11\cdot 7)^2\). Следовательно, \(3,415104=1,848\). Следовательно, уравнение можно переписать в виде: \[(1+4x)(1+2x)(1+x)=1,848\]
Так как \(y\) кратно десяти, то \(y=10; \ 20; \ 30\) и т.д. Следовательно, \(x=\frac1{10}; \ \frac1{5}; \ \frac3{10}\) и т.д. Подставляя по очереди эти числа, видим, что первое значение \(x=\frac1{10}=0,1\) подходит: \[(1+0,4)(1+0,2)(1+0,1)=1,848 \quad\Leftrightarrow\quad 1,848=1,848\] Следовательно, \(y=10\).
Ответ: 10
При каких значениях параметра \(a\) уравнение
\[\cos x+\dfrac32 \cos \dfrac{2x}3+3\cos \dfrac x3=a\]
имеет решения.
1) Рассмотрим функцию \(f(x)=\cos x+\frac32 \cos \frac{2x}3+3\cos
\frac x3\).
Главный период у \(\cos x\) – это \(2\pi\),
у \(\cos \frac{2x}3\) — это \(\dfrac{2\pi}{\frac23}=3\pi\),
у \(\cos\frac x3\) – это \(\dfrac{2\pi}{\frac13}=6\pi\).
Тогда главный период всей функции \(f(x)\) – это НОК этих периодов, то есть \(6\pi\).
2) Для того, чтобы уравнение имело решения, необходимо, чтобы на любом отрезке длиной \(6\pi\) выполнялось: \(\mathrm{min}\,f(x)\leqslant a\leqslant \mathrm{max}\,f(x)\). Возьмем, например, отрезок \([0;6\pi]\).
3) Найдем критические точки функции и построим ее схематичный график для того, чтобы понять, чему равно \(\mathrm{min}\,f(x)\) и \(\mathrm{max}\,f(x)\).
\(f'(x)=\sin x+\sin \dfrac{2x}3+\sin \dfrac x3=0\quad \Rightarrow \quad \left(\sin x+\sin \dfrac{x}3\right)+\sin \dfrac{2x}3=0 \quad \Rightarrow\)
\(\Rightarrow \quad 2\sin \dfrac{2x}3\cos \dfrac x3+\sin \dfrac{2x}3=0 \quad \Rightarrow \quad \sin \dfrac{2x}3\left(2\cos \dfrac x3+1\right)=0\quad \Rightarrow \)
\(\Rightarrow \quad \left[ \begin{gathered} \begin{aligned} &\dfrac{2x}3=\pi n, n\in\mathbb{Z}\\[3pt] & \dfrac x3=\pm \dfrac{2\pi}3+2\pi k, k\in\mathbb{Z} \end{aligned} \end{gathered} \right. \quad \Rightarrow \quad \left[ \begin{gathered} \begin{aligned} &x=\dfrac32\pi n, n\in\mathbb{Z}\\[3pt] &x=\pm 2\pi+6\pi k, k\in\mathbb{Z} \end{aligned} \end{gathered} \right.\)
Промежутку \([0;6\pi]\) принадлежат точки \(0;\ \frac{3\pi}2;\ 2\pi;\
3\pi;\ 4\pi; \ \frac{9\pi}2;\ 6\pi\). Значит, знаки производной такие:
Значит, минимальное значение на \([0;6\pi]\) функция принимает в одной из точек \(\frac{3\pi}2;\ 3\pi;\ \frac{9\pi}2\), а максимальное — в одной из \(0;\ 2\pi;\ 4\pi; \ 6\pi\).
\(\begin{aligned} &f(0)=f(6\pi)=\dfrac{11}2\\[4pt] &f\left(\dfrac{3\pi}2\right)=f\left(\dfrac{9\pi}2\right)=-\dfrac32\\[4pt] &f(2\pi)=f(4\pi)=-\dfrac54\\[4pt] &f(3\pi)=-\dfrac52 \end{aligned}\)
Тогда на \([0;6\pi]\) схематично функция выглядит так:
То есть \(\mathrm{min}\,f(x)=-\dfrac52, \ \mathrm{max}\,f(x)=\dfrac{11}2\). Значит, \(a\in\left[-\dfrac52;\dfrac{11}2\right]\).
Ответ:
\(a\in \left[-\dfrac52;\dfrac{11}2\right]\)
Известно, что многочлен \(P(x)\) имеет вид: \(P(x) = ax^2 + bx + c\).
а) Доктор Ватсон узнал числа \(P(0)\), \(P(1)\), \(P(-1)\). Может ли он однозначно восстановить \(P(x)\)?
б) Джим Мориарти знает числа \(P(0)\), \(P(1)\), \(P(2)\). Он собирается восстановить \(P(x)\). Какой ответ он должен получить?
в) Шерлок Холмс утверждает, что если и можно восстановить \(P(x)\), зная только числа \(P(n - 1)\), \(P(n)\), \(P(n + 1)\) для какого-то целого \(n\), то он находится однозначно. Прав ли он?
Для того, чтобы найти \(P(x)\), необходимо и достаточно найти числа \(a\), \(b\), \(c\). Попробуем найти их.
а)
\[\begin{aligned} \begin{cases} &P(0) = c\\ &P(1) = a + b + c\\ &P(-1) = a - b + c \end{cases} \end{aligned}\]
Тогда \[\dfrac{P(1) + P(-1)}{2} = a + c = a + P(0)\qquad\Rightarrow\qquad a = \dfrac{P(1) + P(-1)}{2} - P(0)\,,\] откуда \[P(1) = a + b + c = \dfrac{P(1) + P(-1)}{2} + b\qquad\Rightarrow\qquad b = \dfrac{P(1) - P(-1)}{2}\]
Подставляя полученные \(a\), \(b\) и \(c\) в исходную систему, убеждаемся, что они действительно подходят.
б)
\[\begin{aligned} \begin{cases} &P(0) = c\\ &P(1) = a + b + c\\ &P(2) = 4a + 2b + c \end{cases} \end{aligned}\]
Тогда \[P(2) - 2P(1) = 2a - c = 2a - P(0)\qquad\Rightarrow\qquad a = 0,5P(0) - P(1) + 0,5P(2)\,,\] таким образом, \[b = P(1) - a - c = P(1) - (0,5P(0) - P(1) + 0,5P(2)) - P(0) = -1,5P(0) + 2P(1) - 0,5P(2)\]
Подставляя полученные \(a\), \(b\) и \(c\) в исходную систему, убеждаемся, что они действительно подходят, следовательно, \[P(x) = (0,5P(0) - P(1) + 0,5P(2))x^2 + (-1,5P(0) + 2P(1) - 0,5P(2))x + P(0)\,.\]
в) Покажем, что Шерлок Холмс прав:
\[\begin{aligned} \begin{cases} &P(n - 1) = a(n - 1)^2 + b(n - 1) + c\\ &P(n) = an^2 + bn + c\\ &P(n + 1) = a(n + 1)^2 + b(n + 1) + c\,, \end{cases} \end{aligned}\]
тогда
\[\begin{aligned} \dfrac{P(n - 1) + P(n + 1)}{2} = a\cdot\dfrac{(n - 1)^2 + (n + 1)^2}{2} + bn + c = a(n^2 + 1) + bn + c = P(n) + a\,, \end{aligned}\]
тогда
\[\begin{aligned} a = \dfrac{P(n - 1) + P(n + 1)}{2} - P(n)\,. \end{aligned}\]
Рассмотрим разность \(P(n + 1) - P(n)\):
\[\begin{aligned} P(n + 1) - P(n) = a(2n + 1) + b\qquad\Rightarrow\qquad b = P(n + 1) - P(n) - a(2n + 1)\,, \end{aligned}\]
но число \(a\) нам уже известно, тогда отсюда находим \(b\). Кроме того, имеем: \[P(n) = an^2 + bn + c\qquad\Rightarrow\qquad c = P(n) - an^2 - bn\,,\] но \(a\) и \(b\) нам известны, следовательно, находим \(c\).
Таким образом, искомые числа \(a\), \(b\) и \(c\), если они существуют, находятся однозначно.
Ответ:
а) Да
б) \((0,5P(0) - P(1) + 0,5P(2))x^2 + (-1,5P(0) + 2P(1) - 0,5P(2))x + P(0)\)
в) Да