19. Задачи на теорию чисел
Какое наибольшее число трёхклеточных уголков можно вырезать из клетчатого квадрата \(8\times 8\)?
Так как, всего на шахматной доске 64 клетки, то вырезать больше 21 уголка не получится, так как \(22\cdot 3 = 66 > 64\).
Это мы провели оценку, то есть доказали что больше 21 уголка вырезать точно не получится. Но это нам не гарантирует, что мы сможем врезать 21 уголок, поэтому мы должны привести пример, как можно вырезать 21 уголок из клетчатого квадрата \(8\times 8\).
Вот пример:
Ответ: 21
Имеется 8 кучек камней, причем во всех кучах число камней разное (куча может состоять из любого, не меньшего 1, числа камней). Известно, что любую из куч можно убрать и все камни из нее разложить по другим кучам так, чтобы число камней в них стало одинаковым. Какое наименьшее число камней может быть в самой большой куче?
(Задача от подписчиков)
Пусть \(a_i\), где \(i=1...8\) – число камней в каждой куче после того, как кучи упорядочили по возрастанию числа камней в них. То есть \(a_1<a_2<...<a_8\). Тогда \(a_1\geqslant 1\) (следует из условия), \(a_2\geqslant 2, \dots, a_8\geqslant 8\).
Пусть мы взяли первую кучу и раскладываем из нее камни по остальным кучам так, чтобы количество в них стало одинаковым. Тогда, так как во всех кучах разное количество камней, наилучший исход (наименьшее количество камней в 1-ой куче) для нас будет таким: ничего не класть в 8-ую кучу, положить 1 камень в 7-ую, 2 камня в 6-ую, 3 камня в 5-ую, 4 камня в 4-ую, 5 камней в 3-ю и 6 камней во 2-ую. Следовательно, в первой куче должно быть как минимум \(1+2+3+4+5+6\) камней. То есть \(a_1\geqslant 21\). Следовательно, \(a_2\geqslant 22\) и т.д., \(a_8\geqslant 28\).
Утверждаем, что наименьшее возможное количество камней в большой куче – 28. Приведем пример: пусть у нас есть 8 куч камней, в которых 21, 22, 23, 24, 25, 26, 27, 28 камней соответственно.
Разложение 1-ой кучи по остальным мы уже продемонстрировали выше. Аналогично можно проверить, что это условие выполняется для любой другой кучи: после разложения камней в оставшихся семи кучах будет по 28 камней.
Ответ: 28
Какое наименьшее число клеточек на доске \(8\times 8\) можно закрасить в черный цвет так, чтобы была хотя бы одна закрашенная клетка
а) в любом квадратике \(2\times 2\)
б) в любом уголке из трёх клеточек?
а) Разобьем шахматную доску на \(16\) клеток \(2\times 2\) как показано на рисунке
Так как всего квадратов \(2\times 2\) 16 штук, то минимальное количество закрашенных клеток 16 (так как если мы закрасим всего 15 клеток, то в каком то из 16 квадратов \(2\times 2\) не будет закрашенной клетки).
Это была оценка, то есть доказательство того, что меньше 16 клеток закрасить мы не сможем.
Пример того, как это можно сделать ниже:
б) Воспользуемся разбиением шахматной доски из пункта а).
Заметим, что если в каком-то из 16 квадратов будет закрашена только 1 клетка, то в этом квадрате \(2\times 2\) обязательно будет уголок из трех клеточек, в котором не будет закрашенной клетки. Поэтому в каждом из 16 квадратов \(2\times 2\) должно быть как минимум 2 закрашенные клетки, то есть всего 32 закрашенные клетки.
Это была оценка, то есть доказательство того, что меньше чем 32 клетки закрасить нам не удастся.
Пример для 32 на рисунке ниже:
Ответ:
a) 16
б) 32.
В странном кинозале места образуют треугольник: в первом ряду одно место, во втором ряду два места, ..., в \(n\)-ом ряду \(n\) мест. Известно, что число мест в кинозале положительно и делится на \(2017\). Какое наименьшее количество стульев может быть в таком зале?
Пусть в зале \(n\) рядов, тогда число стульев в зале равно \[1 + 2 + ... + n = \dfrac{n(n + 1)}{2} = k\cdot 2017\] – для некоторого натурального \(k\). Так как число \(2017\) простое, то один из множителей \(n\) и \((n + 1)\) должен делиться на \(2017\).
При этом ясно, что для того, чтобы количество стульев было минимальным из возможных, необходимо и достаточно, чтобы имело место равенство \((n + 1) = 2017\). Само количество стульев в этом случае равно \[\dfrac{2016\cdot (2016 + 1)}{2} = 2\,033\,136\,.\] Такой вот кинозал...
Ответ: 2033136
Паша пытается в равенстве \(\text{ДЫРА} = \text{ЯМА} + \text{ЯМА} + ... + \text{ЯМА}\) заменить буквы какими-нибудь цифрами, кроме нуля (разные буквы разными цифрами, одинаковые – одинаковыми) так, чтобы “в дыре было как можно больше ям”. Какой ответ у него получится, если он правильно решит поставленную задачу?
Минимальное значение, которое может принимать \(\text{ЯМА}\), равно \(123\). Тогда количество ям не может быть больше \(81\), ведь \(123\cdot 82 = 10086\) – пятизначное число.
При этом количество ям не может быть и \(81\), иначе даже при \(\text{ЯМА} = 123\) получится, что \(\text{ДЫРА}\) не меньше, чем \(9963\), но в слове \(\text{ДЫРА}\) первые две буквы должны заменяться разными цифрами, а числа, не меньшие \(9963\), либо имеют первыми двумя цифрами девятки, либо по крайней мере пятизначны, следовательно, не подходят нам.
В случае, когда количество ям равно \(80\), последняя буква в слове \(\text{ДЫРА}\) обязательно соответствует цифре \(0\), которая у Паши запрещена, следовательно, количество ям не превосходит \(79\).
При этом в случае, когда \(\text{ЯМА} = 125\) и количество ям равно \(79\), получаем: \(\text{ДЫРА} = 9875\), что подходит по условию.
Таким образом, если Паша правильно решит поставленную задачу, он получит ответ \(79\).
Ответ: 79
Илья испёк себе круглый блин. Он решил разрезать его на части, сделав ровно три разреза (разрез идёт “от края до края”) и получить при этом \(8\) частей (не обязательно равных)
а) Сможет ли Илья сделать задуманное?
б) На какое наибольшее количество частей Илья сможет разрезать блин тремя разрезами?
а) Первый разрез разрезает блин ровно на две части.
Второй разрез может пройти по каждой из уже имеющихся частей не более, чем один раз. Таким образом, после второго разреза количество частей не превосходит четырёх.
Третий разрез также может пройти по каждой из имеющихся теперь частей не более, чем один раз. Таким образом, после третьего разреза количество частей не превосходит восьми.
При этом для того, чтобы количество частей стало \(8\), необходимо, чтобы после двух разрезов стало \(4\) части, а третий разрез прошёл по каждой из этих четырёх частей. Докажем от противного, что так быть не может: пусть нам удалось сделать такой третий разрез, тогда через точку пересечения первых двух разрезов мысленно построим разрез, параллельный третьему.
Пусть третий разрез не был параллелен какому-то из первых двух, тогда мысленный разрез прошёл лишь через \(2\) части из четырёх первоначальных, но те две части, через которые он не прошёл, лежат по разные стороны от него, следовательно, перенося его параллельно (до тех пор, пока он не совпадёт с третьим разрезом), мы будем удалять его от одной из частей, через которую он и не проходил.
Аналогичное рассуждение имеет место в случае, когда третий разрез оказался параллельным одному из первых двух.
Таким образом, наш третий разрез не мог пройти через все \(4\) имевшихся до него части, то есть количество частей после него не может быть больше \(7\).
б) Решение для \(7\) частей приведено ниже:
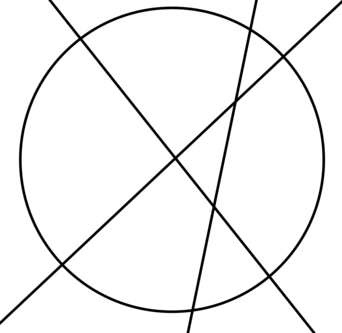
Ответ:
а) Нет
б) 7
Какое наибольшее количество слонов можно поставить на Ванину шахматную доску так, чтобы они не били друг друга, если Ванина доска имеет размеры \(10\times 10\), а каждый слон бьёт любого другого слона при первой же возможности?
Каждый слон простреливает целиком любую диагональ, на которой он находится. Найдём количество попарно параллельных диагоналей на Ваниной доске. Их \(19\). Таким образом, количество слонов не может превышать \(19\) (иначе какие-то два слона оказались бы на одной диагонали и били бы друг друга).
Можно ли расставить \(19\) слонов так, чтобы условие задачи было выполнено? Заметим, что слон, стоящий на чёрной клетке, ходит только по чёрным клеткам, а слон, стоящий на белой клетке, ходит только по белым клеткам. Если можно расставить \(19\) слонов, то найдутся не менее \(10\) слонов, стоящих на клетках одного цвета (пусть для примера это будет чёрный цвет). Но тогда можно поставить и \(10\) слонов на белые клетки, для этого достаточно вертикально приподнять всех слонов, стоящих на чёрных клетках, затем повернуть под ними доску на \(90^\circ\) (вокруг точки пересечения диагоналей квадратной доски) и опустить слонов.
Если слоны, стоявшие до поворота доски на чёрных клетках, не били друг друга, то и после поворота доски они не будут бить друг друга. При этом слоны, стоящие на чёрных клетках, никак не связаны со слонами, стоящими на белых клетках (“они живут в разных мирах”). Тогда можно поставить на доску не менее \(10\) чёрных слонов и не менее \(10\) белых слонов так, что все они не будут бить друг друга, но такого быть не может, следовательно, наше предположение неверно и на такой доске можно расставить не более \(18\) слонов так, чтобы они не били друг друга.
\(18\) слонов можно расставить, например, так: ставим слонов в каждую клетку верхней горизонтали, затем в каждую клетку нижней горизонтали, кроме угловых.
Ответ: 18
