\(SABCD\) – прямоугольная пирамида, вписанная в цилиндр, а \(ABCD\) – квадрат, \(SB\)– высота. Площадь боковой поверхности цилиндра равна \(36\pi\), а его объем равен \(72\pi\). Найдите объем пирамиды.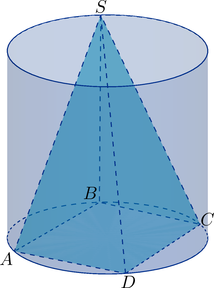
Если разделить объем цилиндра на площадь боковой поверхности, то можно найти радиус окружностей, лежащих в основаниях цилиндра: \[\frac{V_{\text{цил.}}}{S_{\text{бок.пов.}}} = \frac{\pi R^2 H}{2\pi R H} = \frac{R}{2} = \frac{72\pi}{36\pi} = 2\] \(\Rightarrow\) \(R = 4\). Зная радиус, можно выразить высоту: \(2\pi4 H = 36\pi\) \(\Rightarrow\) \(H = 4,5\). Так как точка пересечения диагоналей квадрата совпадает с центром описанной вокруг него окружности, то диагональ квадрата равна диаметру окружности. Площадь квадрата можно найти как половину произведения диагоналей, тогда объем пирамиды равен: \[V_{SABCD} = \frac{1}{3} H \frac{1}{2}(2R)(2R) = \frac{1}{3} 4,5 \frac{1}{2}8^2 = 48\]
Ответ: 48