3. Геометрия на плоскости (планиметрия). Часть I
Биссектриса параллелограмма — это отрезок, соединяющий вершину параллелограмма с точкой на одной из двух противоположных сторон и делящий угол при вершине пополам.
\(\bullet\) Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
\(\bullet\) Биссектрисы соседних углов параллелограмма взаимно перпендикулярны: \(BL\perp AN\).
\(\bullet\) Биссектрисы противоположных углов параллелограмма параллельны: \(AN\parallel CP\).
Биссектрисы углов \(B\) и \(C\) параллелограмма \(ABCD\) пересекаются на стороне \(AD\). Найдите \(BC\), если \(AB=4\).
По свойству биссектрисы параллелограмма \(\triangle ABK\) и \(\triangle
CDK\) – равнобедренные (\(AB=AK\), \(CD=DK\)). Следовательно, \[BC=AD=AK+DK=AB+CD=2AB=8.\]
Ответ: 8
В параллелограмме \(ABCD\) проведены биссектрисы \(AN\) и \(BM\), \(\angle ABM = 58^{\circ}\). Найдите \(\angle BAN\). Ответ дайте в градусах.
Сумма односторонних углов при параллельных прямых и секущей равна \(180^{\circ}\), тогда \(\angle DAB + \angle ABC = 180^{\circ}\).
Так как \(AN\) и \(BM\) – биссектрисы, то \(\angle BAN + \angle ABM = 0,5(\angle DAB + \angle ABC) = 90^{\circ}\).
\(\angle ABM = 58^{\circ}\), тогда \(\angle BAN = 90^{\circ} - 58^{\circ} = 32^{\circ}\).
Ответ: 32
В параллелограмме \(ABCD\) проведена биссектриса \(AN\), точка \(N\) лежит на стороне \(BC\), причём \(NC = 3\), \(AB = 5\). Найдите периметр параллелограмма \(ABCD\).
Так как внутренние накрест лежащие углы при параллельных прямых и секущей равны, то \(\angle BNA = \angle NAD\).
Так как \(AN\) – биссектриса, то \(\angle NAD = \angle BAN\), откуда получаем \(\angle BNA = \angle BAN\).
Таким образом, треугольник \(ABN\) – равнобедренный, \(BN = AB\), тогда \(BC = BN + NC = 5 + 3 = 8\). В итоге, периметр параллелограмма \(ABCD\) равен \(8 + 8 + 5 + 5 = 26\).
Ответ: 26
В параллелограмме \(ABCD\) на стороне \(BC\) выбрана точка \(N\) так, что \(AB = BN\), \(\angle B = 150^{\circ}\). Найдите \(\angle NAD\). Ответ дайте в градусах.
Так как в равнобедренном треугольнике углы при основании равны, то \(\angle BAN = \angle BNA\).
Так как сумма углов в треугольнике равна \(180^{\circ}\), то \(\angle BAN = \angle BNA = 15^{\circ}\).
Так как внутренние накрест лежащие углы при параллельных прямых и секущей равны, то \(\angle NAD = \angle BNA = 15^{\circ}\).
Ответ: 15
В параллелограмме \(ABCD\) биссектриса, выходящая из вершины \(B\), пересекает \(AD\) в точке \(K\) и равна 6. \(\angle BAD = 60^\circ\), \(AK:KD = 3:2\). Найдите периметр параллелограмма \(ABCD\).
\(\angle ABK = \angle KBC\) т.к. \(BK\) – биссектриса \(\angle ABC\). \(\angle KBC = \angle BKA\), т.к. это накрест лежащие углы при параллельных прямых. Тогда:
\[\angle ABK=\angle BKA =\frac{1}{2}(180^\circ-\angle BAD)=\frac{1}{2}(180^\circ-60^\circ)=60^\circ\]
\(\triangle ABK\) равносторонний, значит \(AB = BK = AK = 6\). Тогда \(AK:KD = 6:KD = 3:2 \Rightarrow KD = 4\). \(AD = AK + KD = 10\), тогда:
\[P_{ABCD} = 2\cdot6 + 2\cdot10 = 32\]
Ответ: 32
В параллелограмме \(ABCD\) биссектриса \(\angle BAD\) пересекает сторону \(BC\) в точке \(K\) и делит ее пополам, а также пересекает продолжение стороны \(DC\) в точке \(L\). Найдите периметр параллелограмма, если \(CL = 3\).
\(\triangle CKL = \triangle BKA\) и являются равнобедренными. \[AB = CL = 3, \,\,\, BC = BK + KC = 2\cdot CK = 2\cdot CL = 2\cdot 3 = 6.\] Тогда \(P_{ABCD} = 2\cdot3 + 2\cdot6 = 18\).
Ответ: 18
В параллелограмме \(ABCD\): точка \(K\) лежит на стороне \(AD\), \(BK = 3\) – биссектриса \(\angle ABC\), \(BC = 5\), \(\angle BKA = 60^\circ\). Найдите периметр параллелограмма.
\(\angle ABK = \angle BKA = 60^\circ\) \(\Rightarrow\) \(\angle BAD = 60^\circ\) \(\Rightarrow\) \(\triangle ABK\) – равносторонний, тогда \(AB = BK = 3\) \(\Rightarrow\) \(P_{ABCD} = 2\cdot3 + 2\cdot5 = 16\).
Ответ: 16
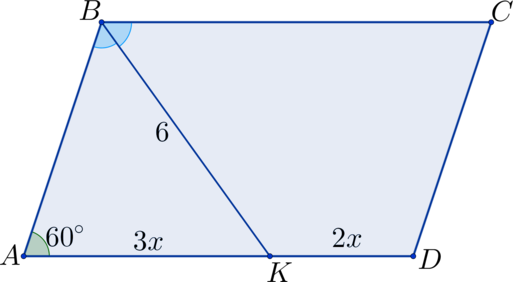
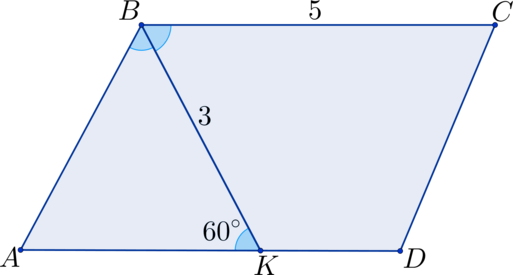
Выпускники, которые рассчитывают успешно сдать ЕГЭ, в обязательном порядке должны повторить тему «Свойства биссектрисы параллелограмма». Как показывает статистика, при прохождении аттестационного испытания задачи по данному разделу планиметрии вызывают сложности у большого количества учащихся. При этом задания, в которых необходимо применить свойства биссектрисы угла параллелограмма, встречаются в ЕГЭ ежегодно. Таким образом, справляться с ними должны все учащиеся.
Образовательный портал «Школково» предлагает выстроить процесс подготовки к прохождению аттестационного испытания по-новому. Занимаясь вместе с нашим ресурсом, выпускники смогут определить наиболее сложные для себя темы и ликвидировать пробелы в знаниях.
Чтобы задания ЕГЭ не вызывали трудностей, рекомендуем вначале повторить основные понятия и свойства биссектрисы параллелограмма. Найти этот материал учащиеся смогут в разделе «Теоретическая справка».
Для того чтобы окончательно понять принцип решения задач по данному разделу планиметрии, мы рекомендуем выполнить соответствующие упражнения. Большая подборка заданий различного уровня сложности представлена в разделе «Каталог». Для каждого упражнения на сайте приведен алгоритм решения и дан правильный ответ. Последовательно выполняя их, учащиеся смогут понять, как правильно применять свойства биссектрисы внутреннего угла параллелограмма.
Получать новые знания и оттачивать собственные навыки по данной теме или, например, в решении задач на тему «Прямоугольник» в ЕГЭ учащиеся могут в онлайн-режиме, находясь в Москве или любом другом российском городе. При необходимости задание можно сохранить в разделе «Избранное». Благодаря этому вы сможете быстро найти интересующие примеры и обсудить алгоритмы нахождения правильного ответа с преподавателем.
