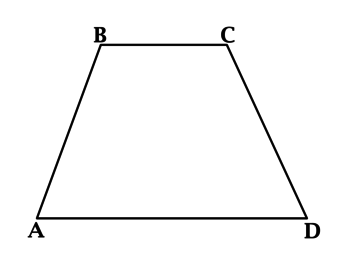
Учащимся старших классов, которые готовятся сдавать ЕГЭ по математике, в обязательном порядке стоит повторить тему «Равнобедренная трапеция» и освежить в памяти ее основные свойства и признаки. Многолетняя практика показывает, что подобные задания ежегодно встречаются в программе аттестационного испытания. Поэтому, если вы хотите успешно решить задачи ЕГЭ на применение основных свойств диагоналей или углов равнобедренной трапеции, вам непременно стоит разобраться в этой теме.
Образовательный портал «Школково» предлагает новый подход к подготовке к аттестационному испытанию. Наш ресурс позволяет учащимся определить наиболее сложные темы и ликвидировать имеющиеся пробелы в знаниях. Специалисты «Школково» подготовили и изложили весь материал в максимально доступной форме.
Чтобы выпускники могли успешно справляться с геометрическими задачами, мы рекомендуем вспомнить определение равнобедренной трапеции, свойства ее сторон, углов и диагоналей, а также формулу для вычисления площади. Эта информация представлена в разделе «Теоретическая справка».
Вспомнив основные свойства углов, диагоналей и сторон равнобедренной трапеции, учащиеся имеют возможность закрепить усвоенный материал, выполнив практические задания. Упражнения различного уровня сложности представлены в разделе «Каталог». В каждом из них вы найдете подробный алгоритм решения и правильный ответ.
Практиковаться в выполнении заданий по теме «Трапеция» при подготовке к ЕГЭ выпускники могут в режиме онлайн, находясь не только в Москве, но и в любом другом городе России. В случае необходимости любое упражнение можно сохранить в разделе «Избранное». Благодаря этому вы сможете быстро найти интересующие примеры и обсудить алгоритмы нахождения правильного ответа с преподавателем.