Выпускники, которые планируют сдавать ЕГЭ по математике и при этом рассчитывают на получение достойных баллов по итогам его прохождения, непременно должны научиться справляться с задачами на нахождение квадратичной функции. Как показывает практика, подобные задания ежегодно встречаются в аттестационном испытании. Если одним из ваших слабых мест являются именно задачи на квадратичную функцию, вам непременно стоит повторить или вновь разобраться в материале.
«Прокачать» навыки и улучшить собственные знания по данной теме вам поможет образовательный проект «Школково». Мы подготовили и систематизировали весь необходимый материал для подготовки к сдаче аттестационного испытания.
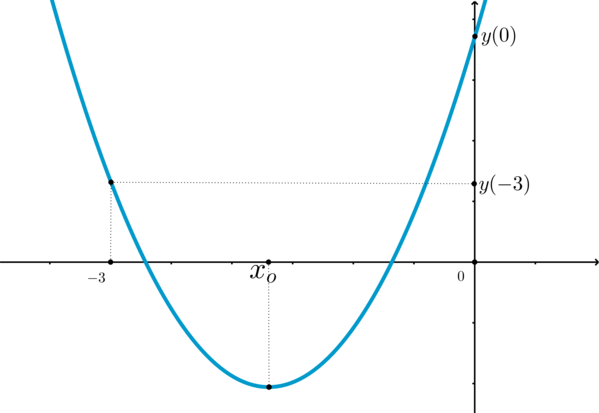
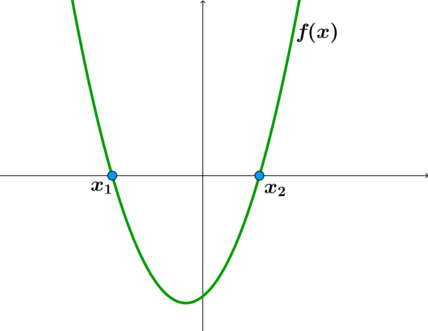
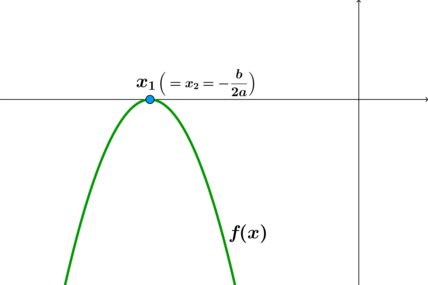
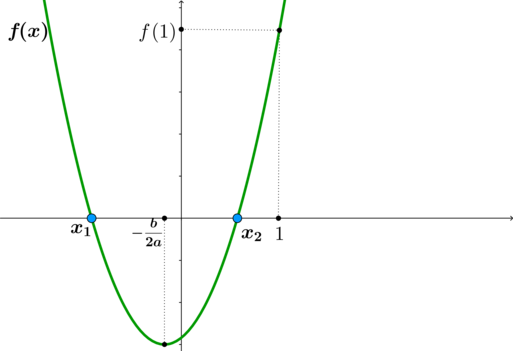
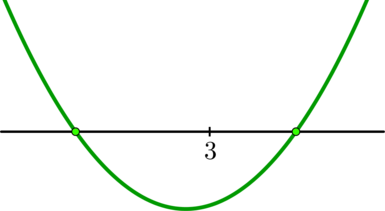
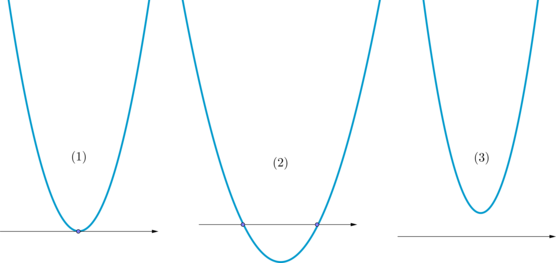
Для того чтобы школьники могли оперативно находить правильные ответы в задачах, ориентируясь на график квадратичной функции, мы предлагаем прежде всего повторить основные понятия и правила. Сделать это вы можете в разделе «Теоретическая справка». Там представлены определение графика квадратичной функции и базовые формулы, необходимые для решения задач по данной теме.
Чтобы получить практические навыки и закрепить полученные знания, предлагаем выполнить упражнения, подобранные нашими специалистами. Для каждой задачи на квадратичную функцию на портале вы найдете правильный ответ и описание алгоритма решения. Практиковаться можно как с простыми упражнениями, так и с более сложными.
Тренироваться в решении задач на квадратичную функцию, которые встречаются в ЕГЭ, школьники могут в режиме онлайн как в Москве, так и в любом другом городе России. При необходимости задание можно сохранить в разделе «Избранное». Благодаря этому вы сможете быстро найти интересующие примеры и обсудить алгоритмы нахождения правильного ответа с преподавателем.