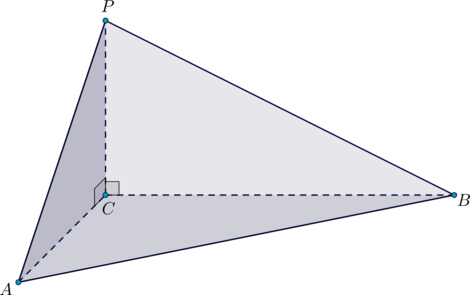
В цилиндре на окружности нижнего основания отмечены точки \(A\) и \(B\). На окружности верхнего основания отмечены точки \(B_1\) и \(C_1\) так, что \(BB_1\) является образующей цилиндра, перпендикулярной основаниям, а \(AC_1\) пересекает ось цилиндра.
а) Докажите, что прямые \(AB\) и \(B_1C_1\) перпендикулярны.
б) Найдите расстояние между прямыми \(AC_1\) и \(BB_1\), если \(AB=12,
B_1C_1=9, BB_1=8\).
(ЕГЭ 2018, основная волна)
а) Пусть \(C\) – проекция точки \(C_1\) на плоскость нижнего основания. Так как \(AC_1\) пересекает ось \(OO_1\) цилиндра, то она лежит с ней в одной плоскости, то есть \(AC_1\) лежит в плоскости осевого сечения цилиндра, следовательно, \(AC\) – диаметр нижнего основания.
Так как \(B_1C_1\parallel (ABC)\), то \(\angle (AB, B_1C_1)=\angle (AB,
BC)\). Так как \(AC\) – диаметр, то \(\angle ABC\) вписанный, опирающийся на диаметр, следовательно, \(\angle ABC=90^\circ\). Чтд.
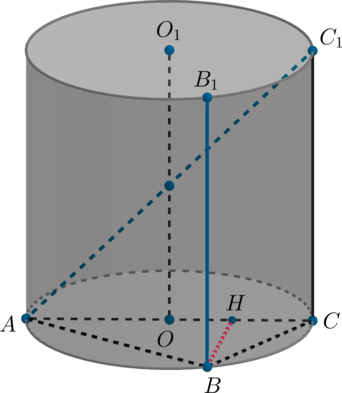
б) Заметим, что прямые \(BB_1\) и \(AC_1\) являются скрещивающимися, так как \(BB_1\parallel (ACC_1)\), а \(AC_1\in (ACC_1)\).
Расстояние между скрещивающимися прямыми в таком случае равно расстоянию от любой точки прямой \(BB_1\) до плоскости \((ACC_1)\). Проведем \(BH\perp AC\). Так как \(OO_1\perp (ABC)\), следовательно, \(OO_1\perp BH\). Таким образом, мы имеем две прямые в плоскости \(ACC_1\), которым перпендикулярна \(BH\). Значит, \(BH\) – расстояние от точки \(B\) до плоскости \(ACC_1\), то есть искомое расстояние.
Так как \(B_1C_1=9\) и \(B_1C_1\parallel BC\), причем \(BC\) – проекция \(B_1C_1\) на плоскость нижнего основания, то \(BC=9\). Отсюда по теореме Пифагора \(AC=\sqrt{AB^2+BC^2}=15\). Тогда из \(S_{ABC}=0,5
AC\cdot BH=0,5AB\cdot BC\) получаем: \(BH=\dfrac{AB\cdot BC}{AC}=7,2\).
Ответ:
б) 7,2