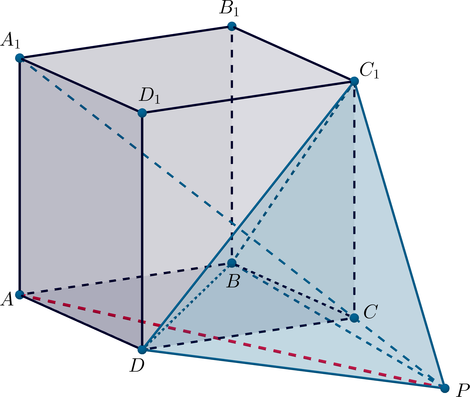
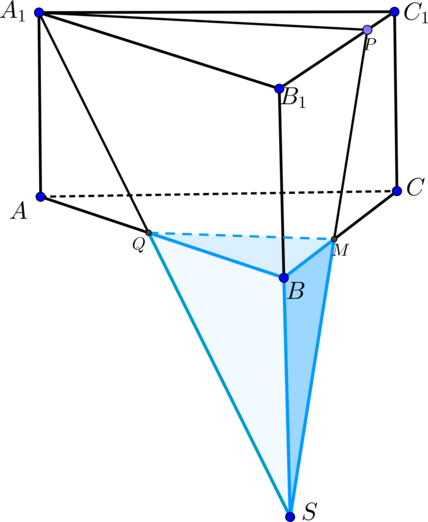
Основанием прямой треугольной призмы \(ABCA_1B_1C_1\) является прямоугольный треугольник \(ABC\), причем \(\angle C=90^\circ\). Известно, что прямая \(A_1C\) перпендикулярна прямой \(AB_1\).
а) Докажите, что \(AA_1=AC\).
б) Найдите расстояние между прямыми \(A_1C\) и \(AB_1\), если известно, что \(AC=7\), \(BC=8\).
(ЕГЭ 2017, основная волна)
а) Заметим, что так как \(B_1C_1\perp A_1C_1\) и \(B_1C_1\perp CC_1\), то \(B_1C_1\perp (AA_1C_1C)\).
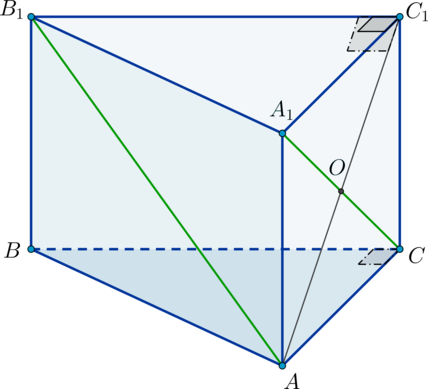
Следовательно, если \(B_1A\) – наклонная, то \(C_1A\) – проекция этой наклонной на плоскость \(AA_1C_1C\). Так как по условию наклонная \(B_1A\) перпендикулярна \(A_1C\), то по теореме о трех перпендикулярах проекция \(C_1A\) также перпендикулярна \(A_1C\), то есть \(A_1C\perp
C_1A\). Следовательно, \(AA_1C_1C\) – прямоугольник, у которого диагонали взаимно перпендикулярны, следовательно, это – квадрат, то есть \(AA_1=AC\), чтд.
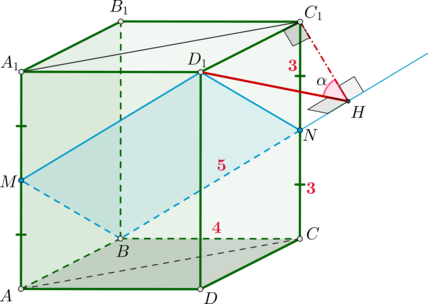
б) Из пункта а) следует, что \(A_1O\perp (AB_1C_1)\) (так как \(A_1O\perp B_1A\) и \(A_1O\perp AC_1\)). Следовательно, \(A_1O\) перпендикулярна любой прямой, лежащей в этой плоскости. Значит, если провести в этой плоскости прямую, перпендикулярную \(B_1A\), то она будет перпендикулярна и \(B_1A\), и \(A_1C\), то есть по определению это и будет прямая, содержащая отрезок, равный расстоянию между \(B_1A\) и \(A_1C\).
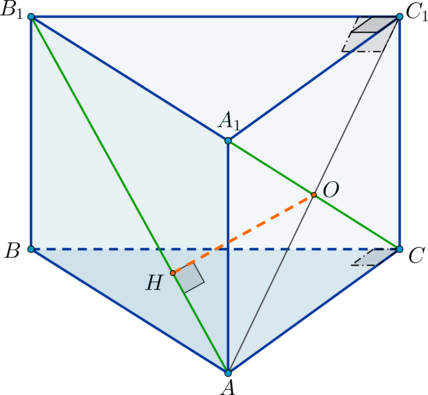
Поэтому проведем \(OH\perp B_1A\). \(OH\) – искомое расстояние.
Заметим, что \(\triangle OHA\sim \triangle AB_1C_1\) по двум углам, следовательно, \[\dfrac{OH}{B_1C_1}=\dfrac{OA}{AB_1}\quad\Rightarrow\quad
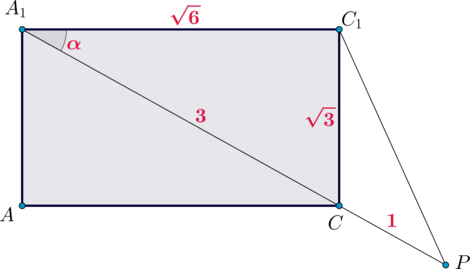
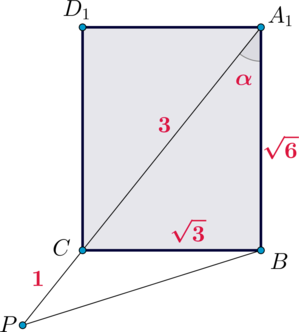
OH=\dfrac{B_1C_1\cdot OA}{AB_1}\] Так как из условия \(BC=8\), то и \(B_1C_1=8\). Так как по доказанному \(AA_1C_1C\) – квадрат со стороной \(AC=7\), то диагональ \(AC_1=7\sqrt2\), следовательно, \(AO=3,5\sqrt2\).
По теореме Пифагора \(AB^2=AC^2+BC^2=7^2+8^2=113\). Снова по теореме Пифагора \(AB_1^2=AB^2+BB_1^2=113+7^2=162\), следовательно, \(AB_1=9\sqrt2\). Таким образом, \[OH=\dfrac{8\cdot 3,5\sqrt2}{9\sqrt2}=\dfrac{28}9\]
Ответ:
б) \(\frac{28}9\)