Можно ли расположить \(12\) одинаковых монет вдоль стенок большой квадратной коробки так, чтобы вдоль каждой стенки лежало ровно
а) по \(2\) монеты;
б) по \(3\) монеты;
в) по \(4\) монеты;
г) по \(5\) монет;
д) по \(6\) монет;
е) по \(7\) монет?
(Разрешается класть монеты одну на другую).
а) Заметим, что если вдоль каждой стенки будет стоять по две монеты, то всего монет будет не больше \(8\), а у нас их \(12\), значит нельзя.
б)–д) В этих пунктах можно расположить монеты требуемым образом. Примеры расстановки приведены на рисунках: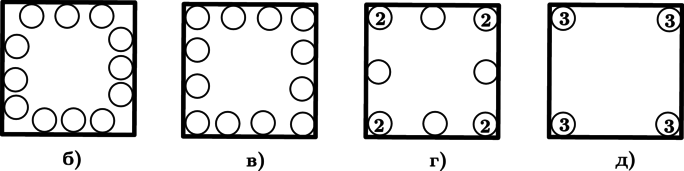
г) Заметим, что каждая монета может стоять максимум около двух стенок коробки, и даже если мы поставим по \(7\) монет одна на другую (оптимальная расстановка), то всего монет будет \(14\), а у нас их \(12\) – противоречие.
Ответ:
а), е) Нельзя; б), в), г), д) можно.



