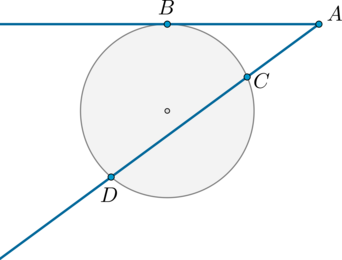
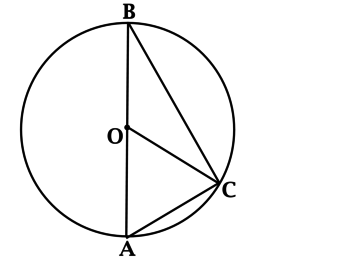
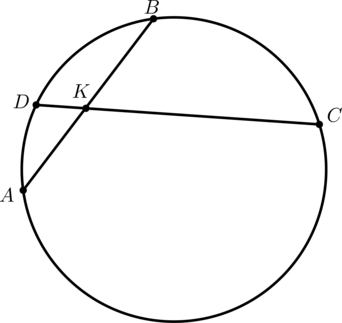
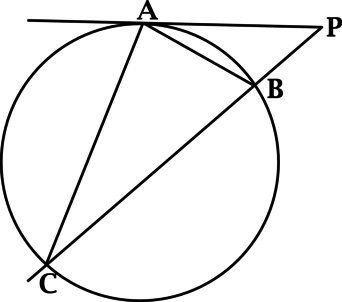
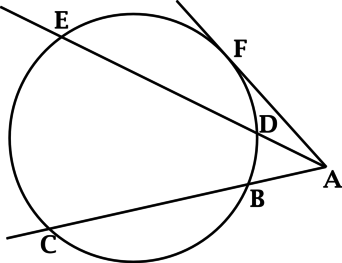
Если старшеклассник готовится к сдаче ЕГЭ по математике базового уровня и при этом рассчитывает на получение конкурентных баллов, ему непременно стоит повторить все теоремы, связанные с длинами отрезков.
Как показывает практика, подобные планиметрические задания включаются в аттестационное испытание каждый год. Это означает, что справляться с задачами ЕГЭ на применение теорем, связанных с длинами отрезков, должны все выпускники, независимо от уровня их подготовки.
Полезная информация
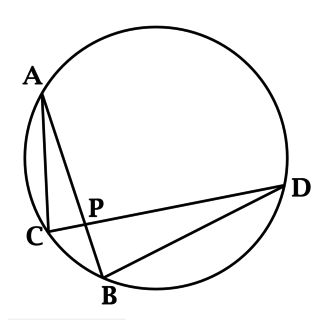
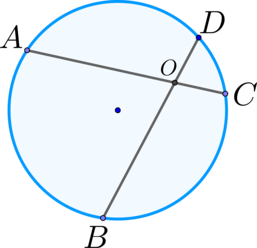
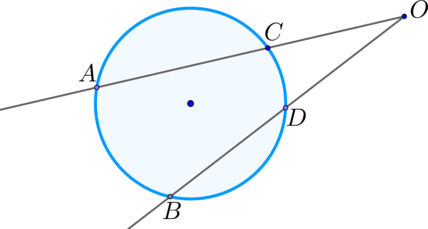
Для того чтобы решить задачи ЕГЭ с применением теорем, связанных с длинами отрезков, рекомендуется следовать определенного алгоритму. Сначала стоит выполнить чертеж. Затем нужно нанести на него все известные параметры исходя из условия задачи. После этого стоит вспомнить относящиеся к ним понятия и теоремы. Затем отразите на чертеже все соотношения между элементами, которые следуют из них логически. Сопоставив имеющиеся параметры, вы сможете найти правильный ответ.
Как подготовиться к экзамену?
Планиметрические задачи вызывают у вас сложность? Образовательный портал «Школково» поможет восполнить пробелы в знаниях. На нашем сайте учащиеся смогут найти и повторить материал, который вызывает затруднения. Наши специалисты собрали и изложили всю теоретическую информацию в максимально доступной и понятной форме.
Все упражнения на сайте, например, задачи на тему «Окружность в ЕГЭ», содержат подробный алгоритм решения и правильный ответ. Выполнять простые и более сложные задания школьники из Москвы и других городов могут в режиме онлайн. Любое задание в случае необходимости возможно сохранить в разделе «Избранное». Это позволит в дальнейшем вернуться к нему для обсуждения с преподавателем или репетитором.