\[{\Large{\text{Центральные и вписанные углы}}}\]
Определения
Центральный угол – это угол, вершина которого лежит в центре окружности.
Вписанный угол – это угол, вершина которого лежит на окружности.
Градусная мера дуги окружности – это градусная мера центрального угла, который на неё опирается.
Теорема
Градусная мера вписанного угла равна половине градусной меры дуги, на которую он опирается.
Доказательство
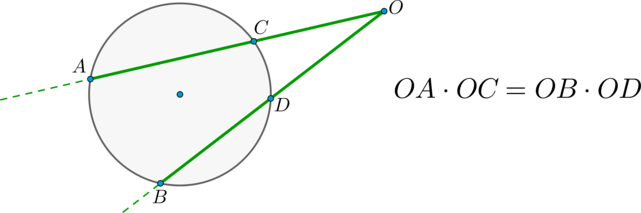
Доказательство проведём в два этапа: сначала докажем справедливость утверждения для случая, когда одна из сторон вписанного угла содержит диаметр. Пусть точка \(B\) – вершина вписанного угла \(ABC\) и \(BC\) – диаметр окружности:
Треугольник \(AOB\) – равнобедренный, \(AO = OB\), \(\angle AOC\) – внешний, тогда \(\angle AOC = \angle OAB + \angle ABO = 2\angle ABC\), откуда \(\angle ABC = 0,5\cdot\angle AOC = 0,5\cdot\buildrel\smile\over{AC}\).
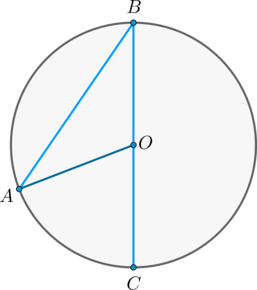
Теперь рассмотрим произвольный вписанный угол \(ABC\). Проведём диаметр окружности \(BD\) из вершины вписанного угла. Возможны два случая:
1) диаметр разрезал угол на два угла \(\angle ABD, \angle CBD\)(для каждого из которых теорема верна по доказанному выше, следовательно верна и для исходного угла, который является суммой этих двух и значит равен полусумме дуг, на которые они опираются, то есть равен половине дуги, на которую он опирается). Рис. 1.
2) диаметр не разрезал угол на два угла, тогда у нас появляется ещё два новых вписанных угла \(\angle ABD, \angle CBD\), у которых сторона содержит диаметр, следовательно, для них теорема верна, тогда верна и для исходного угла (который равен разности этих двух углов, значит, равен полуразности дуг, на которые они опираются, то есть равен половине дуги, на которую он опирается). Рис. 2.
Следствия
1. Вписанные углы, опирающиеся на одну и ту же дугу, равны.
2. Вписанный угол, опирающийся на полуокружность, прямой.
3. Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.
\[{\Large{\text{Касательная к окружности}}}\]
Определения
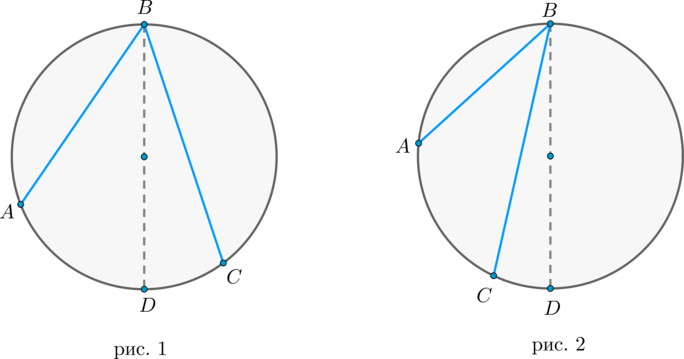
Существует три типа взаимного расположения прямой и окружности:
1) прямая \(a\) пересекает окружность в двух точках. Такая прямая называется секущей. В этом случае расстояние \(d\) от центра окружности до прямой меньше радиуса \(R\) окружности (рис. 3).
2) прямая \(b\) пересекает окружность в одной точке. Такая прямая называется касательной, а их общая точка \(B\) – точкой касания. В этом случае \(d=R\) (рис. 4).
3) прямая \(c\) не имеет общих точек с окружностью (рис. 5).
Теорема
1. Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.
2. Если прямая проходит через конец радиуса окружности и перпендикулярна этому радиусу, то она является касательной к окружности.
Следствие
Отрезки касательных, проведенных из одной точки к окружности, равны.
Доказательство
Проведем к окружности из точки \(K\) две касательные \(KA\) и \(KB\):
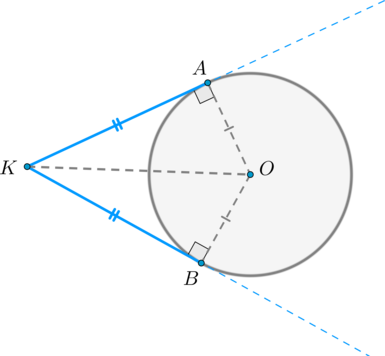
Значит, \(OA\perp KA, OB\perp KB\) как радиусы. Прямоугольные треугольники \(\triangle KAO\) и \(\triangle KBO\) равны по катету и гипотенузе, следовательно, \(KA=KB\).
Следствие
Центр окружности \(O\) лежит на биссектрисе угла \(AKB\), образованного двумя касательными, проведенными из одной точки \(K\).
\[{\Large{\text{Теоремы, связанные с углами}}}\]
Теорема об угле между секущими
Угол между двумя секущими, проведенными из одной точки, равен полуразности градусных мер большей и меньшей высекаемых ими дуг.
Доказательство
Пусть \(M\) – точка, из которой проведены две секущие как показано на рисунке:
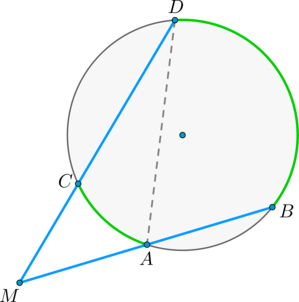
Покажем, что \(\angle DMB = \dfrac{1}{2}(\buildrel\smile\over{BD} -
\buildrel\smile\over{CA})\).
\(\angle DAB\) – внешний угол треугольника \(MAD\), тогда \(\angle DAB =
\angle DMB + \angle MDA\), откуда \(\angle DMB = \angle DAB - \angle
MDA\), но углы \(\angle DAB\) и \(\angle MDA\) – вписанные, тогда \(\angle DMB = \angle DAB - \angle MDA =
\frac{1}{2}\buildrel\smile\over{BD} -
\frac{1}{2}\buildrel\smile\over{CA} =
\frac{1}{2}(\buildrel\smile\over{BD} - \buildrel\smile\over{CA})\), что и требовалось доказать.
Теорема об угле между пересекающимися хордами
Угол между двумя пересекающимися хордами равен полусумме градусных мер высекаемых ими дуг: \[\angle CMD=\dfrac12\left(\buildrel\smile\over{AB}+\buildrel\smile\over{CD}\right)\]
Доказательство
\(\angle BMA = \angle CMD\) как вертикальные.
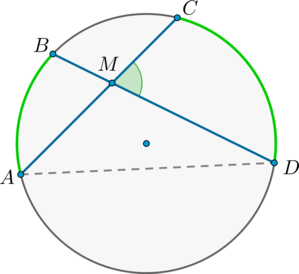
Из треугольника \(AMD\): \(\angle AMD = 180^\circ - \angle BDA - \angle
CAD = 180^\circ - \frac12\buildrel\smile\over{AB} - \frac12\buildrel\smile\over{CD}\).
Но \(\angle AMD = 180^\circ - \angle CMD\), откуда заключаем, что \[\angle CMD = \frac12\cdot\buildrel\smile\over{AB} + \frac12\cdot\buildrel\smile\over{CD}
= \frac12(\buildrel\smile\over{AB} + \buildrel\smile\over{CD}).\]
Теорема об угле между хордой и касательной
Угол между касательной и хордой, проходящей через точку касания, равен половине градусной меры дуги, стягиваемой хордой.
Доказательство
Пусть прямая \(a\) касается окружности в точке \(A\), \(AB\) – хорда этой окружности, \(O\) – её центр. Пусть прямая, содержащая \(OB\), пересекает \(a\) в точке \(M\). Докажем, что \(\angle BAM = \frac12\cdot
\buildrel\smile\over{AB}\).
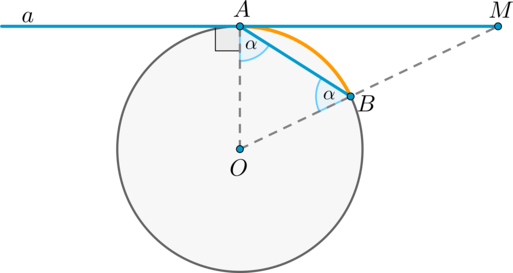
Обозначим \(\angle OAB = \alpha\). Так как \(OA\) и \(OB\) – радиусы, то \(OA = OB\) и \(\angle OBA = \angle OAB = \alpha\). Таким образом, \(\buildrel\smile\over{AB} = \angle AOB = 180^\circ - 2\alpha =
2(90^\circ - \alpha)\).
Так как \(OA\) – радиус, проведённый в точку касания, то \(OA\perp a\), то есть \(\angle OAM = 90^\circ\), следовательно, \(\angle BAM =
90^\circ - \angle OAB = 90^\circ - \alpha =
\frac12\cdot\buildrel\smile\over{AB}\).
Теорема о дугах, стягиваемых равными хордами
Равные хорды стягивают равные дуги, меньшие полуокружности.
И наоборот: равные дуги стягиваются равными хордами.
Доказательство
1) Пусть \(AB=CD\). Докажем, что меньшие полуокружности дуги \(\buildrel\smile\over{AB}=\buildrel\smile\over{CD}\).
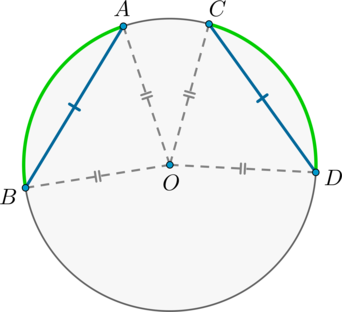
\(\triangle AOB=\triangle COD\) по трем сторонам, следовательно, \(\angle AOB=\angle COD\). Но т.к. \(\angle AOB, \angle COD\) — центральные углы, опирающиеся на дуги \(\buildrel\smile\over{AB},
\buildrel\smile\over{CD}\) соответственно, то \(\buildrel\smile\over{AB}=\buildrel\smile\over{CD}\).
2) Если \(\buildrel\smile\over{AB}=\buildrel\smile\over{CD}\), то \(\triangle AOB=\triangle COD\) по двум сторонам \(AO=BO=CO=DO\) и углу между ними \(\angle AOB=\angle COD\). Следовательно, и \(AB=CD\).
Теорема
Если радиус делит хорду пополам, то он ей перпендикулярен.
Верно и обратное: если радиус перпендикулярен хорде, то точкой пересечения он делит ее пополам.
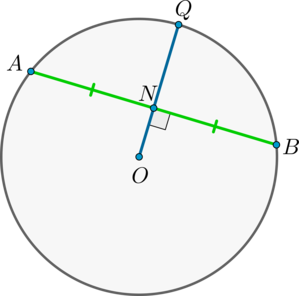
Доказательство
1) Пусть \(AN=NB\). Докажем, что \(OQ\perp AB\).
Рассмотрим \(\triangle AOB\): он равнобедренный, т.к. \(OA=OB\) – радиусы окружности. Т.к. \(ON\) – медиана, проведенная к основанию, то она также является и высотой, следовательно, \(ON\perp AB\).
2) Пусть \(OQ\perp AB\). Докажем, что \(AN=NB\).
Аналогично \(\triangle AOB\) – равнобедренный, \(ON\) – высота, следовательно, \(ON\) – медиана. Следовательно, \(AN=NB\).
\[{\Large{\text{Теоремы, связанные с длинами отрезков}}}\]
Теорема о произведении отрезков хорд
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
Доказательство
Пусть хорды \(AB\) и \(CD\) пересекаются в точке \(E\).
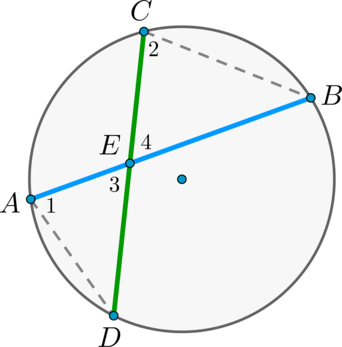
Рассмотрим треугольники \(ADE\) и \(CBE\). В этих треугольниках углы \(1\) и \(2\) равны, так как они вписанные и опираются на одну и ту же дугу \(BD\), а углы \(3\) и \(4\) равны как вертикальные. Треугольники \(ADE\) и \(CBE\) подобны (по первому признаку подобия треугольников).
Тогда \(\dfrac{AE}{EC} = \dfrac{DE}{BE}\), откуда \(AE\cdot BE = CE\cdot DE\).
Теорема о касательной и секущей
Квадрат отрезка касательной равен произведению секущей на ее внешнюю часть.
Доказательство
Пусть касательная проходит через точку \(M\) и касается окружности в точке \(A\). Пусть секущая проходит через точку \(M\) и пересекает окружность в точках \(B\) и \(C\) так что \(MB < MC\). Покажем, что \(MB\cdot MC = MA^2\).
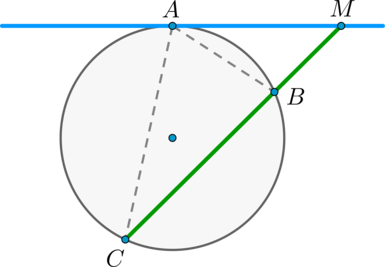
Рассмотрим треугольники \(MBA\) и \(MCA\): \(\angle M\) – общий, \(\angle
BCA = 0,5\cdot\buildrel\smile\over{AB}\). По теореме об угле между касательной и секущей, \(\angle BAM =
0,5\cdot\buildrel\smile\over{AB} = \angle BCA\). Таким образом, треугольники \(MBA\) и \(MCA\) подобны по двум углам.
Из подобия треугольников \(MBA\) и \(MCA\) имеем: \(\dfrac{MB}{MA} = \dfrac{MA}{MC}\), что равносильно \(MB\cdot MC = MA^2\).
Следствие
Произведение секущей, проведённой из точки \(O\), на её внешнюю часть не зависит от выбора секущей, проведённой из точки \(O\):