\[{\Large{\text{Цилиндр}}}\]
Рассмотрим окружность \(C\) с центром \(O\) радиуса \(R\) на плоскости \(\alpha\). Через каждую точку окружности \(C\) проведем прямую перпендикулярно плоскости \(\alpha\). Поверхность, образованная этими прямыми, называется цилиндрической поверхностью.
Сами прямые называются образующими данной поверхности.
Проведем теперь через некоторую точку некоторой образующей плоскость \(\beta\parallel \alpha\). Множество точек, по которым образующие пересекут плоскость \(\beta\), образует окружность \(C'\), равную окружности \(C\).
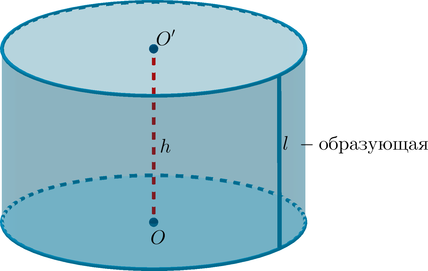
Часть пространства, ограниченная двумя кругами \(K\) и \(K'\) с границами \(C\) и \(C'\) соответственно, а также частью цилиндрической поверхности, заключенной между плоскостями \(\alpha\) и \(\beta\), называется цилиндром.
Круги \(K\) и \(K'\) называются основаниями цилиндра; отрезки образующих, заключенных между плоскостями, – образующими цилиндра; часть цилиндрической поверхности, образованная ими, — боковой поверхностью цилиндра. Отрезок, соединяющий центры оснований цилиндра равен образующей цилиндра и равен высоте цилиндра (\(l=h\)).
Теорема
Площадь боковой поверхности цилиндра равна \[S_{\text{бок.пов-ти цилиндра}}=2\pi R\cdot h\]
где \(R\) – радиус основания цилиндра, \(h\) – высота (образующая).
Теорема
Площадь полной поверхности цилиндра равна сумме площади боковой поверхности и площадей обоих оснований \[S_{\text{полн.пов-ти
цилиндра}}=2\pi R\cdot h+2\pi R^2=2\pi R(R+h)\]
Теорема
Объем цилиндра вычисляется по формуле \[V_{\text{цилиндра}}=\pi R^2\cdot h\]
\[{\Large{\text{Конус}}}\]
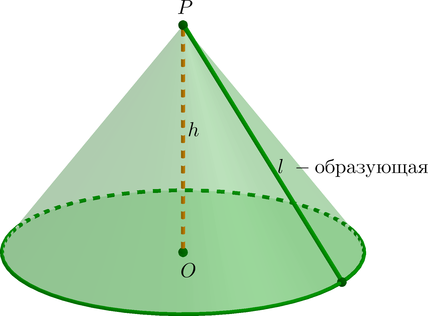
Рассмотрим плоскость \(\alpha\) и на ней окружность \(C\) с центром \(O\) и радиусом \(R\). Через точку \(O\) проведем прямую, перпендикулярную плоскости \(\alpha\). Отметим на этой прямой некоторую точку \(P\). Поверхность, образованная всеми прямыми, проходящими через точку \(P\) и каждую точку окружности \(C\), называется конической поверхностью, а эти прямые – образующими конической поверхности. Часть пространства, ограниченная кругом с границей \(C\) и отрезками образующих, заключенными между точкой \(P\) и точкой на окружности, называется конусом. Отрезки \(PA\), где \(A\in \text{окр. }
C\), называются образующими конуса; точка \(P\) – вершина конуса; круг с границей \(C\) – основание конуса; отрезок \(PO\) – высота конуса.
Замечание
Заметим, что у конуса высота и образующая не равны друг другу, как было в случае с цилиндром.
Теорема
Площадь боковой поверхности конуса равна \[S_{\text{бок.пов-ти конуса}}=\pi R\cdot l\]
где \(R\) – радиус основания конуса, \(l\) – образующая.
Теорема
Площадь полной поверхности конуса равна сумме площади боковой поверхности и площадей основания \[S_{\text{полн.пов-ти
конуса}}=\pi R\cdot l+\pi R^2=\pi R(R+l)\]
Теорема
Объем конуса вычисляется по формуле \[V_{\text{конуса}}=\dfrac13\pi R^2\cdot h\]
Замечание
Заметим, что цилиндр в каком-то смысле является призмой, только в основании находится не многоугольник (как у призмы), а круг.
Формула объема цилиндра такая же, как и формула объема призмы: произведение площади основания на высоту.
Аналогично конус в каком-то смысле является пирамидой. Поэтому формула объема конуса такая же, как и у пирамиды: треть площади основания на высоту.
\[{\Large{\text{Сфера и шар}}}\]
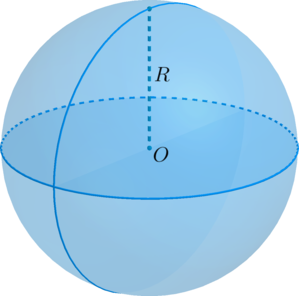
Рассмотрим множество точек пространства, равноудаленных от некоторой точки \(O\) на расстояние \(R\). Это множество называется сферой с центром в точке \(O\) радиуса \(R\).
Отрезок, соединяющий две точки сферы и проходящий через ее центр называется диаметром сферы.
Сфера вместе со своей внутренностью называется шаром.
Теорема
Площадь сферы вычисляется по формуле \[S_{\text{сферы}}=4\pi R^2\]
Теорема
Объем шара вычисляется по формуле \[V_{\text{шара}}=\dfrac43 \pi R^3\]
Определение
Шаровой сегмент – это часть шара, отсекаемая от него некоторой плоскостью.
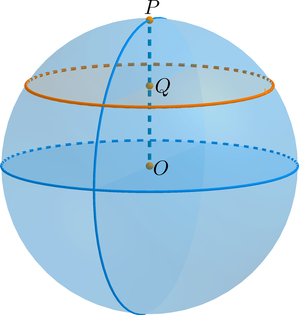
Пусть плоскость пересекла шар по кругу \(K\) с центром в точке \(Q\). Соединим точки \(O\) (центр шара) и \(Q\) и продлим этот отрезок до пересечения со сферой – получим радиус \(OP\). Тогда отрезок \(QP\) называется высотой сегмента.
Теорема
Пусть \(R\) – радиус шара, \(h\) – высота сегмента, то объем шарового сегмента равен \[V_{\text{}}=\pi h^2 (R-\dfrac13h)\]
Определение
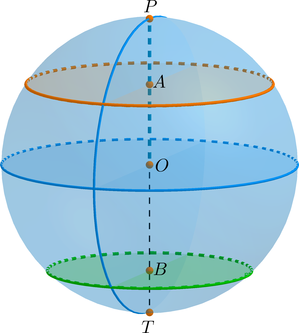
Шаровой слой – это часть шара, заключенная между двумя параллельными плоскостями, пересекающими этот шар. Круги, по которым плоскости пересекают шар, называются основаниями шарового слоя, отрезок, соединяющий центры оснований – высотой шарового слоя.
Две оставшиеся части шара являются в этом случае шаровыми сегментами.
Объем шарового слоя равен разности объема шара и объемов шаровых сегментов с высотами \(AP\) и \(BT\).