Радикальная ось — прямая, проходящая через точки пересечения двух окружностей.
Линия центров окружностей — прямая, проходящая через центры двух окружностей.
Теорема 1.
1) Радикальная ось перпендикулярна линии центров окружностей.
2) Отрезки касательных, проведенных из любой точки радикальной оси к этим окружностям, равны.
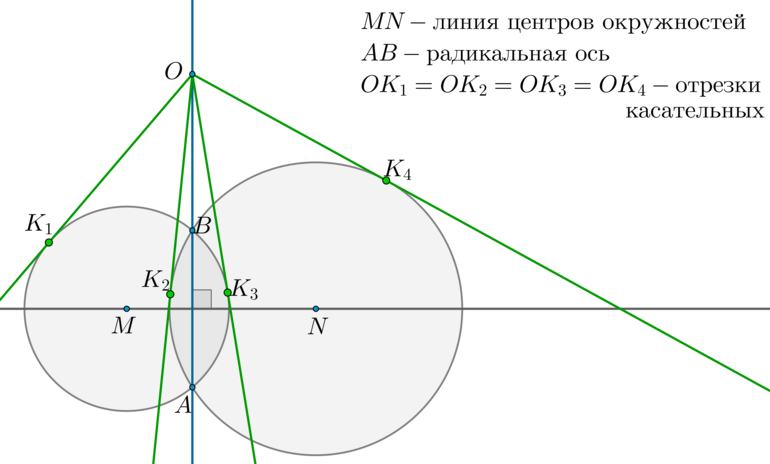
Доказательство:
1) Рассмотрим \(\triangle BMN\) и \(\triangle AMN\): они равны по трем сторонам (\(BM=AM=R_1, BN=AN=R_2\) — радиусы первой и второй окружностей соответственно). Таким образом, \(\angle BNM=\angle ANM\), следовательно, \(MN\) — биссектриса в равнобедренном \(\triangle ANB\), следовательно, \(MN\perp AB\).
2) Отметим произвольную точку \(O\) на радикальной оси и проведем касательные \(OK_1, OK_3\) к первой окружности и \(OK_2, OK_4\) ко второй окружности. Т.к. квадрат отрезка касательной равен произведению секущей на ее внешнюю часть, то \(OK_1^2=OK_2^2=OK_3^2=OK_4^2=OB\cdot OA\).
Теорема 2.
Пусть две окружности с центрами \(M\) и \(N\) касаются внешним образом в точке \(A\). Две общие касательные (внутренняя и внешняя) \(a\) и \(b\) этих окружностей пересекаются в точке \(B\). Точки касания — точки \(A, K_1, K_2\) (как показано на рисунке). Тогда \[(1) \ {\large{K_1B=AB=K_2B}}\] \[(2) \ {\large{\angle K_1AK_2=90^\circ}}\]
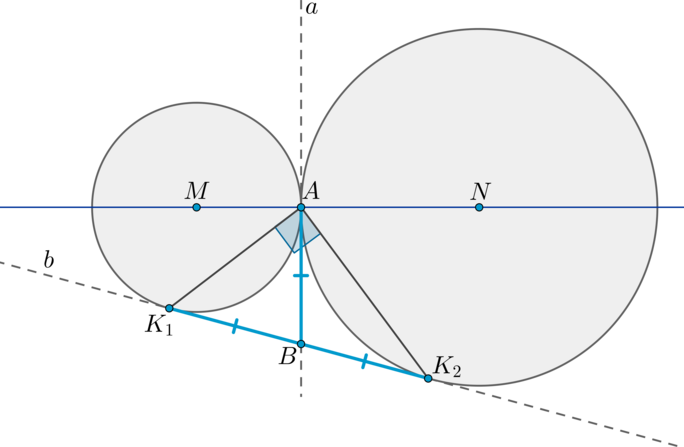
Доказательство:
1) Т.к. \(BA\) и \(BK_1\) — две касательные, проведенные к первой окружности из одной точки, то отрезки касательных равны: \(BA=BK_1\). Аналогично, \(BA=BK_2\). Таким образом, \(BA=BK_1=BK_2\).
2) Значит, \(BA\) — медиана в \(\triangle K_1AK_2\), равная половине стороны, к которой она проведена. Значит, \(\angle A=90^\circ\).
Теорема 3.
Пусть две окружности касаются внешним образом в точке \(A\). Через точку \(A\) проведены две прямые \(B_1B_2\) и \(C_1C_2\), пересекающие каждую окружность в двух точках, как показано на рисунке. Тогда: \[(1) \ {\large{\triangle AB_1C_1 \sim \triangle AB_2C_2}}\] \[(2) \ {\large{B_1C_1\parallel B_2C_2}}\]
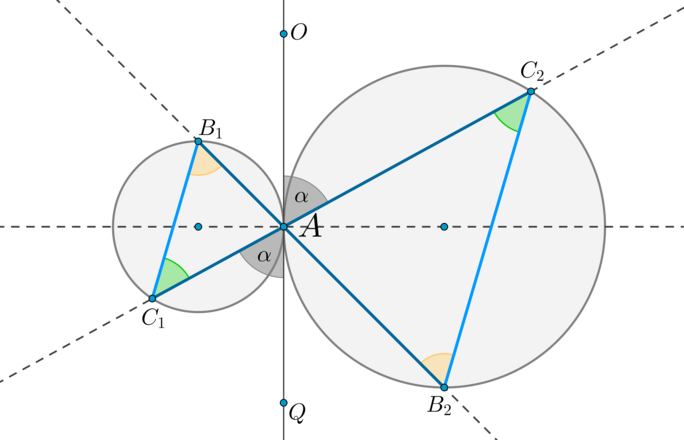
Доказательство:
1) Проведем через точку \(A\) общую касательную этих окружностей \(OQ\). \(\angle OAC_2=\angle QAC_1=\alpha\) как вертикальные. Т.к. угол между касательной и хордой, проведенной через точку касания, равен половине дуги, заключенной между ними, то \(\angle
OAC_2=\frac12\buildrel\smile\over{AC_2}\), \(\angle
QAC_1=\frac12\buildrel\smile\over{AC_1}\). Следовательно, \(\buildrel\smile\over{AC_1}=\buildrel\smile\over{AC_2}=2\alpha\). Таким образом, \(\angle AB_1C_1=\angle AB_2C_2=\alpha\). Значит, по двум углам \(\triangle AB_1C_1\sim \triangle AB_2C_2\).
2) Т.к. \(\angle AB_1C_1=\angle AB_2C_2\), то прямые \(B_1C_1\parallel
B_2C_2\) по накрест лежащим углам при секущей \(B_1B_2\).
Теорема Птолемея
Во вписанном четырехугольнике произведение диагоналей равно сумме произведений противоположных сторон: \[AC\cdot BD=AB\cdot CD+BC\cdot AD\]
Доказательство
Пусть для определенности \(\angle ABD<\angle CBD\). Проведем отрезок \(BO\) так, чтобы \(O\) лежала на \(AC\) и \(\angle ABD=\angle CBO\):
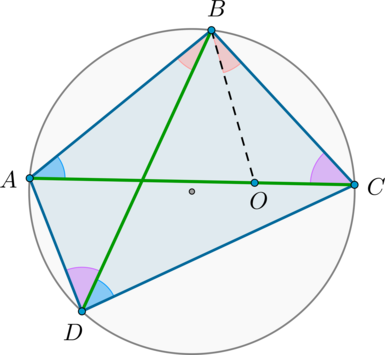
Т.к. \(\angle ACB=\angle ADB\) (опираются на одну и ту же дугу), то по двум углам \(\triangle OBC\sim \triangle ABD\). Значит: \[\dfrac{OC}{AD}=\dfrac{BC}{BD} \Rightarrow AD\cdot BC=OC\cdot BD\phantom{00000000000} (1)\]
Т.к. \(\angle BAC=\angle BDC\) (опираются на одну и ту же дугу), \(\angle ABO=\angle CBD\) (состоят из равных по построению (оранжевых) углов и общего угла \(\angle DBO\)), то по двум углам \(\triangle
ABO\sim \triangle BDC\). Значит: \[\dfrac{AO}{DC}=\dfrac{AB}{BD} \Rightarrow AB\cdot CD=AO\cdot BD \phantom{00000000000} (2)\]
Сложим равенства \((1)\) и \((2)\): \(AD\cdot BC+AB\cdot CD=OC\cdot
BD+AO\cdot BD=AC\cdot BD\), чтд.
Формула Эйлера:
Пусть \(R\) — радиус описанной около треугольника \(ABC\) окружности, \(r\) — радиус вписанной окружности. Тогда расстояние \(d\) между центрами этих окружностей вычисляется по формуле: \[{\large{d^2=R^2-2Rr}}\]
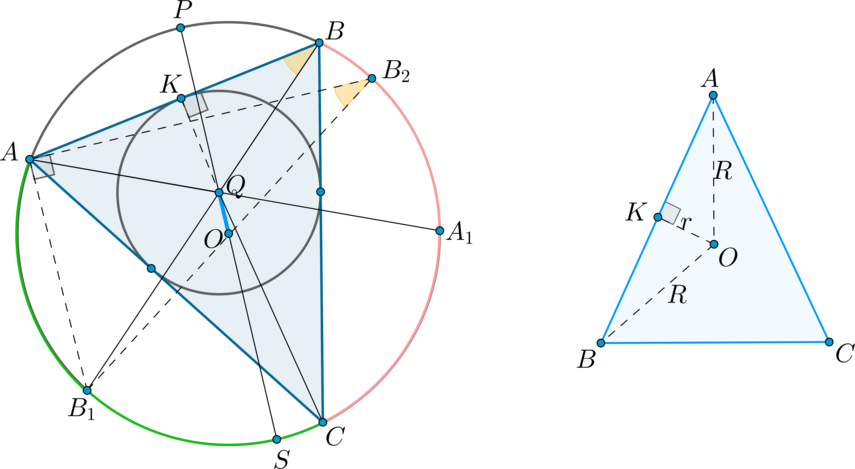
Доказательство:
а) Предположим, что \(d\ne 0\). Пусть \(O, Q\) — центры описанной и вписанной окружности соответственно. Проведем диаметр описанной окружности \(PS\) через точку \(Q\). Проведем также биссектрисы углов \(\angle A, \angle B\) — \(AA_1, BB_1\) соответственно (заметим, что они пересекутся в точке \(Q\), т.к. центр вписанной окружности лежит на пересечении биссектрис). Хорды \(PS\) и \(BB_1\) пересекаются, следовательно, отрезки этих хорд равны: \(PQ\cdot QS=BQ\cdot QB_1\).
Т.к. \(OP=OS=R, OQ=d\), то последнее равенство можно переписать в виде \((R-d)(R+d)=BQ\cdot QB_1 \ (*)\).
Заметим, что т.к. \(AA_1, BB_1\) — биссектрисы, то \(\buildrel\smile\over{AB_1}=\buildrel\smile\over{B_1C}=x, \
\buildrel\smile\over{CA_1}=\buildrel\smile\over{A_1B}=y\). Т.к. угол между хордами равен полусумме дуг, заключенных между ними, то:
\(\angle AQB_1=\frac12(x+y)\).
С другой стороны, \(\angle
B_1AA_1=\frac12\big(\buildrel\smile\over{B_1C}+\buildrel\smile\over{CA_1}\big)=\frac12(x+y)\)
Таким образом, \(\angle AQB_1=\angle B_1AA_1\). Следовательно, \(\triangle QB_1A\) — равнобедренный и \(B_1Q=B_1A\). Значит, равенство \((*)\) можно переписать как:
\(R^2-d^2=BQ\cdot AB_1 \ (**)\).
Проведем еще один диаметр описанной окружности \(B_1B_2\). Тогда \(\triangle B_1AB_2\) — прямоугольный (\(\angle A\) опирается на диаметр). Пусть также вписанная окружность касается стороны \(AB\) в точке \(K\). Тогда \(\triangle BKQ\) — прямоугольный.
Заметим также, что \(\angle KBQ=\angle AB_2B_1\) (т.к. они опираются на одну и ту же дугу).
Значит, \(\triangle B_1AB_2\sim \triangle BKQ\) по двум углам, следовательно:
\(\dfrac{KQ}{AB_1}=\dfrac{BQ}{B_1B_2} \Rightarrow
\dfrac{r}{AB_1}=\dfrac{BQ}{2R} \Rightarrow BQ\cdot AB_1=2Rr\).
Подставим это в \((**)\) и получим:
\(R^2-d^2=2Rr \Rightarrow d^2=R^2-2Rr\).
б) Если \(d=0\), т.е. центры вписанной и описанной окружностей совпадают, то \(AK=BK=\sqrt{R^2-r^2} \Rightarrow AB=2\sqrt{R^2-r^2}\). Аналогично \(AC=BC=AB=\sqrt{R^2-r^2}\), т.е. треугольник равносторонний. Следовательно, \(\angle A=60^\circ \Rightarrow \angle
KAO=30^\circ \Rightarrow r=\frac12R \Rightarrow R=2r\) или \(0=R^2-2Rr\) (т.е. в этом случае формула также верна).
Теорема о бабочке:
Пусть через середину хорды \(AB\) — точку \(O\), проведены две хорды \(MN\) и \(KP\). Пусть \(MP\cap AB=X, KN\cap AB=Y\). Тогда \[{\large{OX=OY}}\]
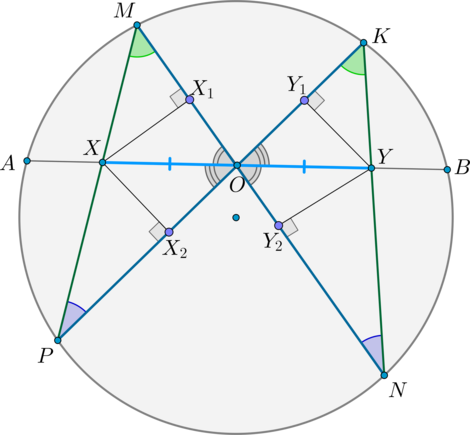
Доказательство:
Проведем перпендикуляры \(XX_1, YY_2\perp
MN, XX_2, YY_1\perp KP\).
Следующие углы равны, т.к. опираются на одну и ту же дугу: \(\angle
PMO=\angle NKO, \angle MPO=\angle KNO\).
Следующие углы равны, т.к. вертикальные: \(\angle XOX_1=\angle YOY_2,
\angle XOX_2=\angle YOY_1\).
Следующие прямоугольные треугольники подобны:
1) \(\triangle XX_1O\sim \triangle YY_2O \Rightarrow
\dfrac{XO}{YO}=\dfrac{XX_1}{YY_2}\)
2) \(\triangle XX_2O\sim \triangle YY_1O \Rightarrow
\dfrac{XO}{YO}=\dfrac{XX_2}{YY_1}\)
3) \(\triangle MXX_1\sim \triangle KYY_1 \Rightarrow
\dfrac{XX_1}{YY_1}=\dfrac{MX}{KY}\)
4) \(\triangle PXX_2\sim \triangle NYY_2 \Rightarrow
\dfrac{XX_2}{YY_2}=\dfrac{PX}{NY}\)
Из 1) и 2) следует, что
\(\dfrac{XO^2}{YO^2}=\dfrac{XX_1\cdot XX_2}{YY_1\cdot YY_2}\)
Из 3) и 4) следует, что
\(\dfrac{XX_1\cdot XX_2}{YY_1\cdot YY_2}=\dfrac{MX\cdot PX}{KY\cdot
NY}\)
Совместив последние два равенства, получим:
\(\dfrac{XO^2}{YO^2}=\dfrac{MX\cdot PX}{KY\cdot NY}\)
Заметим, что для пересекающихся хорд \(AB\) и \(MP\): \(AX\cdot
XB=MX\cdot PX\). Аналогично \(AY\cdot YB=KY\cdot NY\). Значит:
\(\dfrac{XO^2}{YO^2}==\dfrac{AX\cdot XB}{AY\cdot YB}\)
Обозначим \(OX=x, OY=y, OA=OB=t \Rightarrow\)
\(\dfrac{x^2}{y^2}=\dfrac{(t-x)(t+x)}{(t+y)(t-y)}=\dfrac{t^2-x^2}{t^2-y^2}
\Rightarrow x^2t^2-x^2y^2=y^2t^2-x^2y^2 \Rightarrow x^2=y^2
\Rightarrow x=y\).









