Теорема 1:
Если на одной из сторон угла отметить равные между собой отрезки и через их концы провести параллельные прямые, то эти прямые отсекут на второй стороне также равные между собой отрезки.
Доказательство:
Докажем сначала лемму: Если в \(\triangle OBB_1\) через середину \(A\) стороны \(OB\) проведена прямая \(a\parallel BB_1\), то она пересечет сторону \(OB_1\) также в середине.
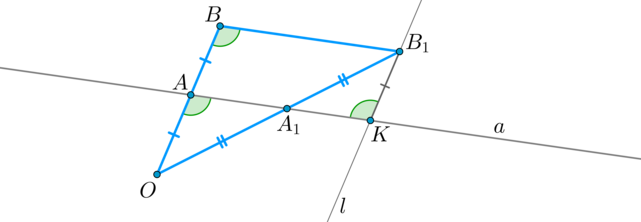
Через точку \(B_1\) проведем \(l\parallel OB\). Пусть \(l\cap a=K\). Тогда \(ABB_1K\) — параллелограмм, следовательно, \(B_1K=AB=OA\) и \(\angle
A_1KB_1=\angle ABB_1=\angle OAA_1\). Значит, по второму признаку \(\triangle OAA_1=\triangle B_1KA_1 \Rightarrow OA_1=A_1B_1\). Лемма доказана.
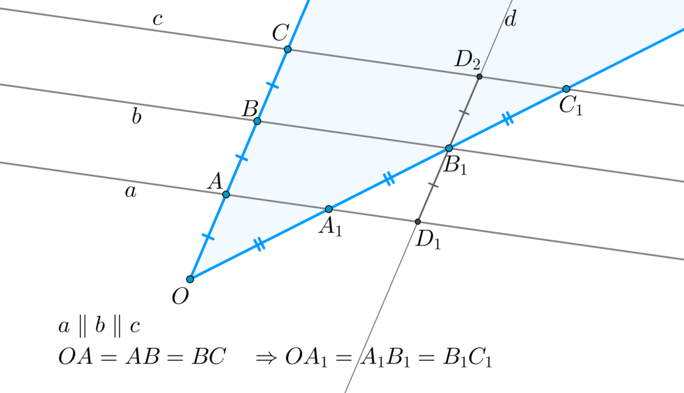
Перейдем к доказательству теоремы. Пусть \(OA=AB=BC\), \(a\parallel
b\parallel c\) и нужно доказать, что \(OA_1=A_1B_1=B_1C_1\).
Таким образом, по данной лемме \(OA_1=A_1B_1\). Докажем, что \(A_1B_1=B_1C_1\). Проведем через точку \(B_1\) прямую \(d\parallel OC\), причем пусть \(d\cap a=D_1, d\cap c=D_2\). Тогда \(ABB_1D_1, BCD_2B_1\) — параллелограммы, следовательно, \(D_1B_1=AB=BC=B_1D_2\). Значит, по первому признаку \(\triangle A_1B_1D_1=\triangle C_1B_1D_2
\Rightarrow A_1B_1=B_1C_1\).
Теорема Фалеса:
Параллельные прямые отсекают на сторонах угла пропорциональные отрезки.
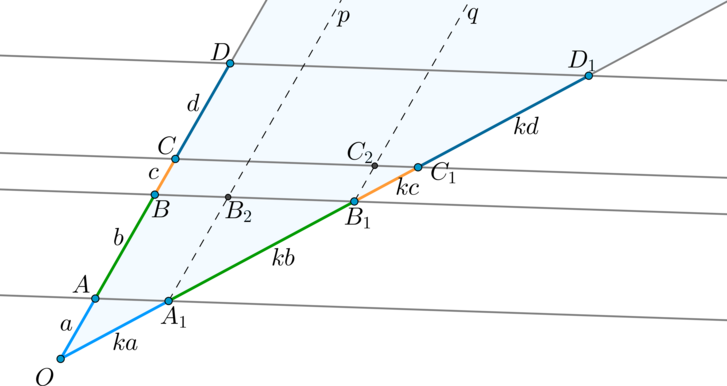
Доказательство:
Пусть параллельные прямые \(p\parallel q\parallel r\parallel s\) разбили одну из прямых на отрезки \(a, b, c, d\). Тогда вторую прямую эти прямые должны разбить на отрезки \(ka,
kb, kc, kd\) соответственно.
Проведем через точку \(A_1\) прямую \(p\parallel OD\) (\(ABB_2A_1\) — параллелограмм, следовательно, \(AB=A_1B_2\)). Тогда \(\triangle OAA_1
\sim \triangle A_1B_1B_2\) по двум углам. Следовательно, \(\dfrac{OA}{A_1B_2}=\dfrac{OA_1}{A_1B_1} \Rightarrow A_1B_1=kb\).
Аналогично проведем через \(B_1\) прямую \(q\parallel OD \Rightarrow
\triangle
OBB_1\sim \triangle B_1C_1C_2 \Rightarrow B_1C_1=kc\) и т.д.
Наиболее часто встречающиеся подобия треугольников:
Теорема 2.
Средняя линия треугольника отсекает от него подобный ему треугольник.

Доказательство:
Т.к. средняя линия — это отрезок, соединяющий середины двух сторон, то \(\dfrac{AB}{A_1B}=\dfrac{CB}{C_1B}=2\).
Таким образом, по двум пропорциональным сторонам и углу между ними (\(\angle B\) — общий) \(\triangle A_1BC_1 \sim \triangle ABC\).
Теорема 3.
Треугольники, образованные диагоналями трапеции и основаниями, подобны.
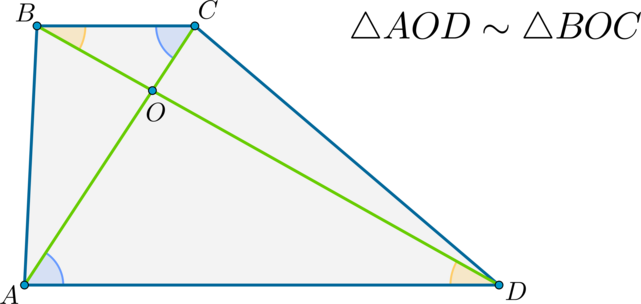
Доказательство:
Т.к. \(AD\parallel BC \Rightarrow \angle OBC=\angle ODA\). \(\angle
BOC=\angle AOD\) как вертикальные. Следовательно, по двум углам \(\triangle BOC\sim \triangle AOD\).
Теорема 4.
Высота прямоугольного треугольника, проведенная к гипотенузе, делит его на два подобных треугольника.
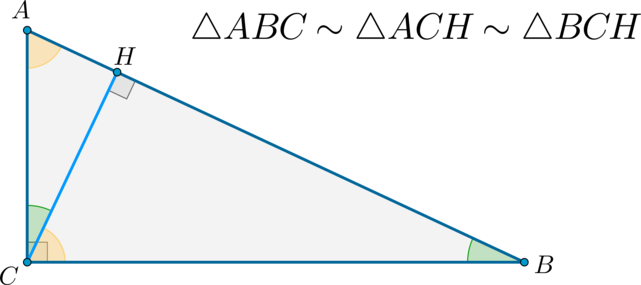
Доказательство:
Обозначим \(\angle ACH=\alpha, \angle BCH=\beta\), т.е. \(\alpha+\beta=90^\circ\). Тогда \(\angle
CAH=90^\circ-\alpha=\beta, \angle CBH=90^\circ-\beta=\alpha\).
Следовательно, по двум углам \(\triangle ACH\sim \triangle BCH\sim
ABC\).
Теорема 5.
Отрезки, соединяющие основания высот треугольника, отсекают от него подобные ему треугольники.
Эти отрезки также являются биссектрисами углов треугольника, вершинами которого являются основания данных высот.
Доказательство:
1) Рассмотрим четырехугольник \(AC_1A_1C\) — около него можно описать окружность, т.к. \(\angle AC_1C=\angle
AA_1C\). Таким образом, \(\angle CAA_1=\angle CC_1A_1=x\), т.к. опираются на одну и ту же хорду \(A_1C\). Таким образом \(\angle
ACA_1=90^\circ-x, \angle BC_1A_1=90^\circ-x \Rightarrow \angle
ACA_1=\angle BC_1A_1\).
Значит, по двум углам \(\triangle A_1BC_1\sim
\triangle ABC\) (\(\angle B\) — общий).
Аналогично доказывается, что \(\triangle AB_1C_1\sim \triangle ABC,
\triangle A_1B_1C\sim \triangle ABC\).
2) Докажем, что \(AA_1, BB_1, CC_1\) – биссектрисы углов \(A_1, B_1,
C_1\) в треугольнике \(A_1B_1C_1\) соответственно.
Обозначим \(\angle BC_1A_1=\angle B_1C_1A=\alpha\). Тогда \(\angle
A_1C_1C=90^\circ -\alpha=\angle B_1C_1C\). Значит, \(CC_1\) – биссектриса угла \(C_1\).
Аналогично доказывается про \(AA_1\) и \(BB_1\).
Теорема 6.
Если к окружности из одной точки вне окружности проведены две секущие, то:
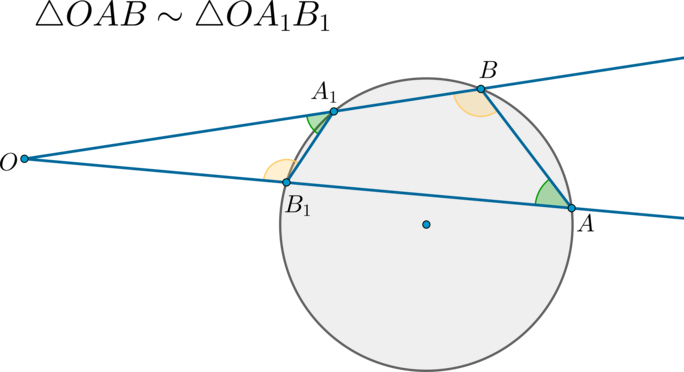
Доказательство:
Четырехугольник \(ABA_1B_1\) описанный, следовательно, \(\angle
BAB_1+\angle BA_1B_1=180^\circ \Rightarrow
\angle OA_1B_1=180^\circ-\angle BA_1B_1=\angle BAB_1\).
Таким образом, по двум углам (\(\angle O\) — общий) \(\triangle
OAB\sim
\triangle OA_1B_1\).
Теорема 7.
Если к окружности из одной точки проведены касательная и секущая, то:
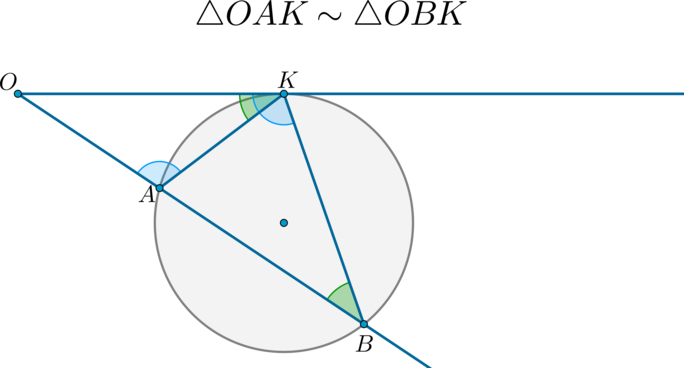
Доказательство:
Т.к. угол между касательной и хордой, проведенной в точку касания, равен половине дуги, заключенной между ними, то \(\angle OKA=\frac12 \buildrel\smile\over{KA}=\angle KBA\).
Следовательно, по двум углам (\(\angle O\) — общий) \(\triangle
OKA\sim \triangle OKB\).
Теорема 8.
Если в окружности две хорды пересекаются, то:
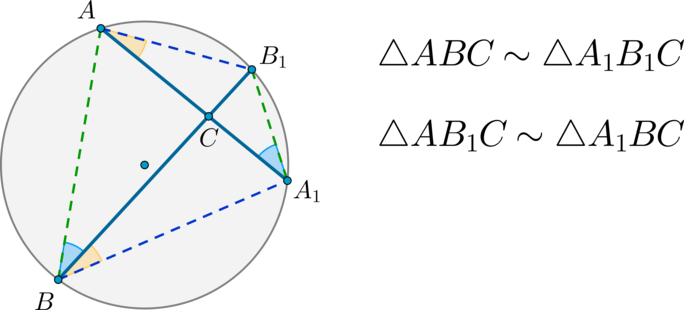
Доказательство:
\(\angle A_1AB_1=\angle A_1BB_1\), т.к. опираются на одну и ту же дугу. \(\angle A_1CB=\angle B_1CA\), т.к. они вертикальные. Следовательно, по двум углам \(\triangle A_1BC\sim
\triangle B_1C\).
Аналогично \(\triangle ABC\sim \triangle A_1B_1C\).












